Introduction
Large Language Models (LLMs) have demonstrated reasoning skills in human tasks, highlighting the importance of their ability to reason. LLMs excel at breaking down problems into parts, making them easier to solve. They are particularly skilled at handling reasoning tasks like solving math word problems. To make the most of LLMs strong reasoning abilities, researchers have proposed prompts and techniques such as chain of thought reasoning and in-context learning.
Exploring methods for verifying outputs has played a role in enhancing LLMs reasoning capabilities. These approaches involve generating paths of reasoning and developing verifiers to evaluate and provide results. However current methods treat each path of reasoning as entities, without considering the interconnections and interactions between them. This paper introduces a graph based approach called Reasoning Graph Verifier (RGV) to examine and validate solutions generated by LLMs, thereby enhancing their reasoning capabilities.
Reasoning of fine-tuning models
Fine tuning models have garnered attention in the field of reasoning tasks particularly when it comes to language models. Researchers have explored approaches to enhance the reasoning capabilities of these tuned language models. These approaches include training language models with a focus on reasoning, training verifiers to rank solutions generated by tuned language models, creating training examples using predefined templates to equip language models with reasoning abilities and continuously improving reasoning capabilities by pre training on program execution data.
Studies have primarily focused on specific reasoning tasks such as reasoning, common sense reasoning and inductive reasoning. Various techniques like tree structured decoders, graph convolutional networks, and contrastive learning have been proposed to improve the performance of language models on reasoning tasks. However it has been observed that multi step reasoning remains a challenge, for both language models and other natural language processing (NLP) models.
Reasoning of large language models
Large language models (LLMs) have demonstrated abilities in reasoning especially when it comes to tasks like solving math word problems. They achieve this by utilizing a chain of thought approach, which enhances their problem solving capabilities and offers insights into their reasoning process. Recent advancements in LLMs indicate that they possess the potential for multi step reasoning, requiring only the appropriate prompt to leverage this capability. Different prompting methods, such as chain of thought, explain then predict, predict then explain, and least to most prompting have been suggested to improve the accuracy of math problem solving and enhance reasoning capabilities.
Apart from prompt design, incorporating strategies like verifiers has played a significant role in enhancing the reasoning abilities of LLMs. The authors introduce a graph based method known as Reasoning Graph Verifier (RGV), which analyzes and verifies solutions generated by LLMs. This RGV method significantly improves their reasoning capabilities and outperforms existing verifier methods in terms of enhancing their performance.
RGV Framework: Reasoning to solve Math Word Problems
The problem at hand revolves around a group of word problems that are described in the written form: Q = {Q1, Q2, ..., Qn}, where each Qi is represented by the
text description of a single math word problem. The main goal is to generate answers for these problems. These answers are expressed as A = {A1, A2, ..., An}. It is worth noting that, the process involves the use of language models that produce sets of reasoning paths for each problem. Each solution in this set is represented as Si = {Q, Step1, Step2... Stepl, A}. In this representation, Q represents the word problem. Steps indicate the intermediate steps involved in reaching a solution step by step, and A represents the answer.
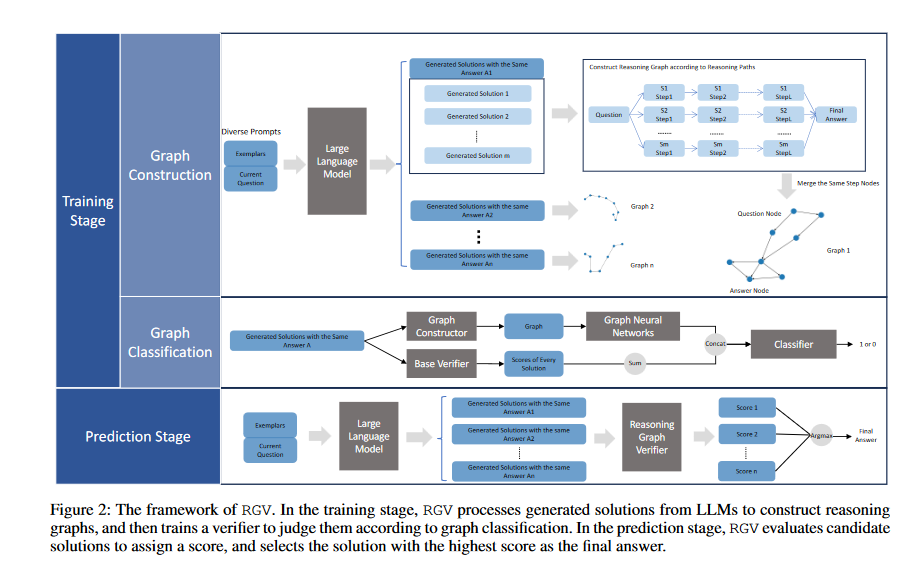
The training process techniques involves two steps: Graph Construction and Graph Classification. In the Graph Construction step, solutions produced by LLMs using prompts are organized, based on their final answers. The reasoning paths are broken down into steps, and any intermediate steps with the same expressions are merged to form reasoning graphs. In the Graph Classification step, these reasoning graphs are classified using an integrated verifier model that considers the sum of scores from the base verifier.
Moving forward to the prediction stage, candidate solutions are generated by LLMs, and treated in the same manner to the training stage. The trained verifier is then used to assess the scores of each candidate solution, ultimately selecting the solution with the highest score as the final predicted answer. This verification method based on graphs significantly enhances LLMs reasoning abilities and outperforms existing verifier methods in terms of improving these models overall reasoning performance.
Prompt Design
Designing efficient prompts is important for enhancing the output of Language Models (LLMs) in providing solutions.
The researchers incorporate LLMs to solve arithmetic word problems by using chain-of-thought and in-context learning. The following equation describes how the language models generate output y from input x:

- The above formula describes the probability of a sequence of tokens 'y' based on the context vector labeled as 'C', and an input sequence 'x'. This probability is determined by the product of the probabilities of each individual token, using the 't' index to locate its position, in the resulting output.
- To estimate the probability of each token, we use a language model called 'pLM' which considers the context vector, input sequence and previously generated tokens up to position 't-1', represented as 'y<t'.
- The symbol ∏t=1∣y∣ represents the product of token probabilities, from position 't=1' to position 't=|y|', where '|y|' indicates the length of the resulting sequence.
- C is a concatenation of k exemplars, denoted as:
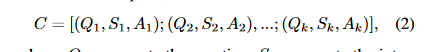
where, Qi represents the question, Si represents the intermediate steps of the solution, and Ai represents the answer. We set k to five in this study, resulting in a prompt that consists of five question-answer pairs sampled from the training split of a math word problem dataset. Therefore, the prompt can be denoted as:

where Q stands for the question in the provided mathematical word problem.
This paper proposes the concept of self-consistency as a solution to the problem of instability and occasional errors in sampling a single output from LLMs. In this process, we will try out different reasoning paths, and then use a vote to settle on the most reliable answers.
Conclusion
In this study, a unique graph-structured verification method, dubbed the Reasoning Graph Verifier (RGV), is introduced. Its primary aim is to bolster the problem-solving abilities of Large Language Models (LLMs), particularly in the realm of mathematical word problems. The RGV scrutinizes and authenticates the answers created by these LLMs by transforming them into reasoning graphs. These graphs skillfully encapsulate the logical ties between the intermediate steps of diverse reasoning paths.
References









