Overview
As we have seen in the previous article, DETR, or Detection Transformer, is a new fangled deep learning model for detecting objects in images. It's an all-in-one model we can train from end to end. DETR does object detection by treating it as a set prediction problem and uses a transformer to process the image features.
Here's a birds-eye view of how it works: DETR starts off with a normal convolutional neural network (CNN) backbone to extract features from the input image, like most vision models. It flattens these features out, adds positional info to show where objects are located in the image, and feeds this into a transformer encoder. After going through the transformer which lets the model understand relationships between the image features, there's a transformer decoder.
A transformer decoder then takes as input a small fixed number of learned positional embeddings, which are called object queries - these help it figure out what objects are present. It attends to the encoded image features from the encoder to predict the object locations and classes. So in a nutshell, DETR replaces the traditional object detection pipeline with a Transformer that directly predicts the objects.
Optimal Bipartite Matching in DETR: Minimizing Set Prediction Loss for Object Detection
The set prediction loss is figured out by using the bipartite matching method, which aligns predicted objects with the ground-truth objects. The technique involves finding the best match between predicted objects and ground-truth objects based on their similarity scores. To get the similarity scores, it looks at the intersection over union (IoU) of the predicted bounding boxes and ground-truth boxes. Using bipartite matching means that each predicted object is paired with, at most, one ground-truth object, and vice versa.
The equation for optimal bipartite matching is defined as:
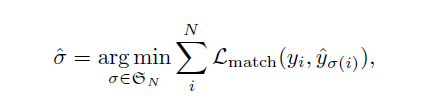
The optimization problem represented by this equation is used to find the optimal permutation of predicted objects, which is then used to output the final set of object predictions.
It's about minimizing the total matching loss between the ground truth objects and the predicted objects, by looking at all the possible permutations of the predictions. It chooses the one that results in the lowest total matching loss.
Instead of using the normal approach where we make region proposals and then classify each region, DETR just makes a set of object predictions all at once for the entire image.
The Role of Hungarian Algorithm in Minimizing Cost
The Hungarian algorithm is regarded as a highly effective solution for addressing the assignment problem, which pertains to finding the optimal assignment of a set of tasks to a set of agents with given costs.
This article serves as an introductory guide on the topic. It aims to expound upon how the Hungarian algorithm functions, while exploring ways in which it might be implemented more efficiently. Neverheless, the steps to compute the Hungarian algorithm can be summarized in the diagram below.
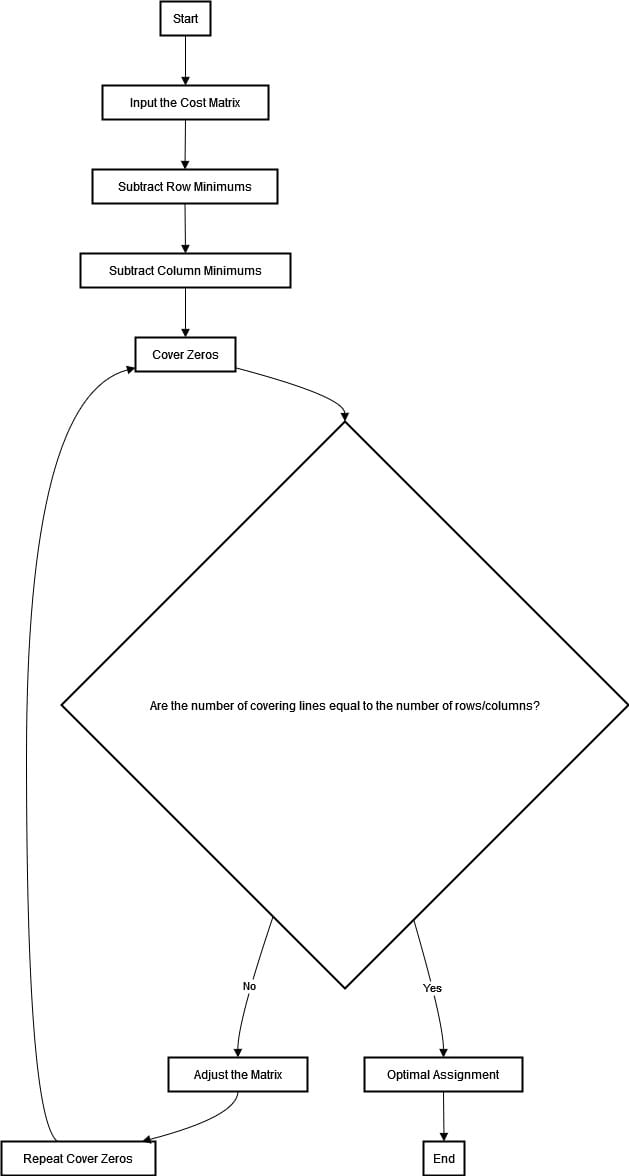
The flowchart for the Hungarian algorithm starts with constructing a cost matrix. Each element represents the cost of assigning a worker to complete a task.
The algorithm follows row reduction, where we subtract the smallest element in each row from all elements within that same row.
We then move on to column reduction and apply this process similarly across columns. Following this step, our next objective is to cover all zero in our matrix with the minimum number of horizontal and vertical lines.
The optimality of the coverage is checked as follows: if the number of lines equals the size of the matrix, then an optimal assignment exists; otherwise, adjustments must be made to the matrix.
The adjustments involve subtracting from all uncovered elements and adding them to any element that's covered by two lines.
This process repeats until there are as many covering lines as for the matrix size. It is then possible to determine an optimal assignment using zero positions in the matrix.
Hungarian algorithm plays an important role in the DETR (DEtection TRansformer) model. The DETR model considers each image as a set of objects, and the Hungarian algorithm is used to associate predictions to the corresponding GT (Ground Truth) objects. Let's visualize the process in the diagram below.
After processing an image, DETR outputs a fixed number of predictions per image. Each prediction comprises a class label and a bounding box. Simultaneously, the model has a set of GT objects for each image, each consisting of a class and a bounding box.
For the Hungarian algorithm to function effectively, a cost matrix is imperative. In DETR, we craft this crucial schema by evaluating and quantifying each prediction vis-à-vis its corresponding ground-truth object to establish an accurate 'cost'. This value serves as an insightful indicator of any incongruence or deviation between prediction and the GT object.
There are two critical factors that contribute to the total cost: The 'class error' and the 'bounding box error'. Class error is essentially the negative log-likelihood of the GT label given the model's predicted class distribution. Bounding box error is the L1 loss between the predicted and GT bounding box coordinates.
By undertaking a meticulous analysis of the cost matrix, The DETR model uses the ingenious Hungarian algorithm with precise craftsmanship. This allows it to find the optimal assignment of predictions that are promptly and accurately mapped onto their respective GT objects. This pioneering approach minimizes the total cost while optimizing overall performance for maximum efficiency.
Hungarian Algorithm and Cost Calculation in DETR
The Hungarian algorithm is used to solve the assignment problem in polynomial time. When eveluating the performance of object detection models, two pivotal parameters come into play:
- Class error, E_c, is calculated using cross-entropy loss: E_c = -log(P(Y=y)), where P(Y=y) is the predicted probability of the GT class.
- Bounding box error, E_b, is simply the L1 loss(sum of absolute differences) between the predicted bounding box coordinates (x_pred, y_pred, w_pred, h_pred) and the GT coordinates (x_gt, y_gt, w_gt, h_gt): E_b = |x_pred - x_gt| + |y_pred - y_gt| + |w_pred - w_gt| + |h_pred - h_gt|.
The total cost, C, is then a weighted sum of the class and bounding box errors:
C = λ*E_c + (1-λ)*E_b, where λ is a weight parameter that balances the contributions of the class and bounding box errors.
Embedded within DETR, lies this formula that encapsulates the essence of the Hungarian algorithm. The crux of this ground-breaking mathematical formula involves assigning each prediction to their corresponding ground truth object while minimizing total cost.
This approach ensures the best possible match between the model's predictions and the actual objects in the image. It's through this technique that DETR exudes its exceptional aptitude for precise object detection. This advanced capability is achieved with seamless fluidity thanks to its innovative end-to-end framework. DERT does away of cumbersome custom components found prevalent among most competing models today.
Transforming Cost Matrices into Profit Matrices for Optimal Object Detection
The Hungarian loss (or Kuhn-Munkres loss, as it’s known in a bigger context) enables a more precise algorithm for object detection as processed in the DETR (Detection Transformer) framework. It's widely acknowledged that computer vision poses challenges when multiple objects possess similar weights or sizes.
To address this concern, the Hungarian loss entails optimization of an assignment problem at the solution level which delineates corresponding ground truth objects and predictions. Of utmost importance here is transforming two matrices into a profit matrix to enable efficient optimization of predictions.
The cost matrix pertains to a matrix with dimensions of p x p, where the quantity designated by 'p' represents the number of resources attributed for carrying out a task. In our particular instance, it relates to predictions and subsequently matches against ground truth objects. A higher cost within this context suggests a worse match quality. For DETR purposes, pair-wise matching costs between image-designated prediction boxes and ground truth are used to compute the cost matrix.
The Hungarian loss algorithm was initially developed to address assignment problems with the objective of maximizing profit. Therefore, it's necessary to convert the cost matrix into a profit matrix. This conversion process involves subtracting each element in the cost matrix from its maximum value. In mathematical terms, this transformation can be expressed as follows:
P_ij = max(C) - C_ij
where P_ij represents the element in the profit matrix, C_ij is the element in the cost matrix, and max(C) is the maximum value in the cost matrix. We can summarize the process below.
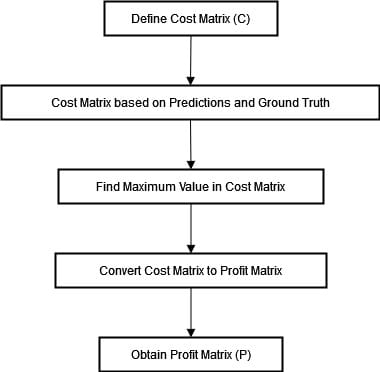
The driving force behind this transformation is the desire to synchronize with the Hungarian algorithm's pursuit of maximizing profits (or, in our instance, reducing costs). By implementing a profit matrix we can accurately measure and gauge the "profitability" of each assignment between a prediction and ground truth, enriching predictive performance. Let's add a practical exemple to the above flowchart.
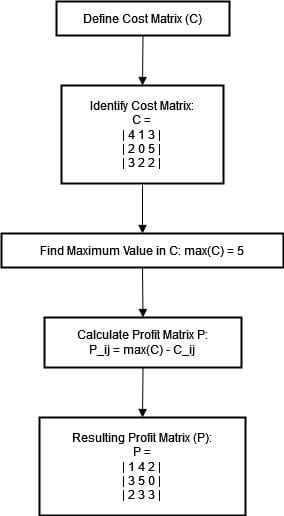
This transformation enhances the algorithm's ability to optimize predictions to ground truth objects because the conversion to a profit matrix helps the model to better understand the implications of each assignment. This way, the Hungarian algorithm can make better decisions in correlating predictions with the ground truth, hence improving detection accuracy.
Use Case: Optimizing E-commerce Image Search with DETR
In an e-commerce platform, accurate object detection within product images is paramount for optimizing user experience. To ensure efficient resource allocation and cost management in such platforms, converting cost matrices into profit matrices is important. The diagram below aims to illustrate the practical implementation benefits of augmenting image search capabilities within e-commerce using these techniques.
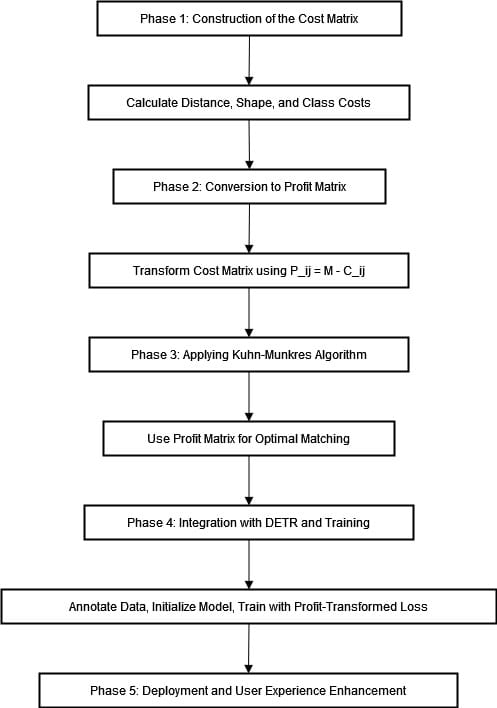
Phase one: Construction of the Cost Matrix
In the first step, a cost matrix is generated where each entry (Cij) represents the cost incurred for associating the predicted object of i-th index with that of j-th ground truth. The calculation of this cost involves various factors such as:
- Distance cost: Calculation based on the Euclidean distance separating the predicted bounding box from its corresponding ground truth bounding box, utilizing a formal and professional approach.
- Shape cost: Discrepancy in aspect ratios or areas between predicted and actual detected bounding boxes.
- Class cost: The accuracy of classification or the confidence score associated with the identified object class.
Phase two: Conversion of Cost to Profit Matrix.
To transform the cost matrix into a profit matrix, it is necessary to perform an inversion of the cost values. This can be achieved through the transformation function denoted by Pij=M−Cij, where M represents a suitably large constant ensuring all profit values are positive. Upon application of this formula, we get the desired profit matrix P which aligns with maximization profits under conditions that prioritize minimization of associated costs.
Phase three: Applying Kuhn-Munkres (Hungarian) Algorithm
Using the profit matrix P, we employ the Kuhn-Munkres algorithm to discern the optimal matching between predicted entities and ground truth ones. This critical stage ensures that the overall assignment maximizes the total profit
Phase four: Integration with DETR and Training
- Data Annotation: Produce a comprehensive ground truth dataset by annotating an assorted collection of product images with precise bounding boxes and clearly defined class labels.
- Model Initialization: The initialization process involves incorporating the profit-to-cost reduction mechanism into the loss function of DETR model. This requires efficient calculation of matching loss by implementing a matching process within the training pipeline.
- Training: Conduct training for the DETR model by utilizing profit-transformed matching loss. This will ensure that it undertakes an optimal approach of determining bounding boxes and classes with enhanced proficiency within maximizing the operation's profitability matrix. This will lead to better object detection capabilities.
Phase five: Deployment and user experience enhancement
Upon completion of its training, the model is subsequently deployed onto the e-commerce platform. Whenever a user makes an image search request, the pipeline proceeds as follows:
- Object Detection: The Object Detection feature of the DETR model applies object recognition techniques to identify and delineate objects present in a given query image. It accurately identifies each detected object by providing corresponding class labels and bounding boxes specifying their geometric location within the image.
- Product Matching: The platform uses an optimal object detection mechanism for product matching, where the detected objects are cross-referenced with inventory data to retrieve pertinent products.
- Display Results: The search algorithm presents the corresponding products to the user with accuracy, improving the relevancy of outcomes and enhancing overall satisfaction among them.
Conclusion
The Hungarian algorithm is the optimization piece that figures out the best overall set of matches based on the similarity scores. It takes the bipartite graph and finds the ideal configuration of matches between the two sides. This is crucial for getting DETR to actually work in practice and match the right visual regions to the right textual queries.
Bipartite matching gives DETR a sound mathematical framework for connecting language and vision, while the Hungarian algorithm find the best matchings within that framework. The two techniques enable DETR to align textual and visual concepts in an optimized way. They're what make the cross-modal matching possible.
References
Hungarian algorithm: A step by step guide to assignment method
The Assignment Problem (Using Hungarian Algorithm)
A. R. Gosthipaty and R. Raha. “DETR Breakdown Part 2: Introduction to DEtection TRansformers,” PyImageSearch, P. Chugh, S. Huot, K. Kidriavsteva, and A. Thanki, eds., 2023, https://pyimg.co/slx2k











