Implementation StyleGAN2 from scratch

In this article, we will make a clean, simple, and readable implementation of StyleGAN2 using PyTorch.

10 months ago • 16 min read

By Abd Elilah TAUIL

Bring this project to life

This article is about StyleGAN2 from the paper Analyzing and Improving the Image Quality of StyleGAN, we will make a clean, simple, and readable implementation of it using PyTorch, and try to replicate the original paper as closely as possible.

If you didn't read the StyleGAN2 paper. or don't know how it works and you want to understand it, I highly recommend you to check out this post blog where I go throw the details of it.

The dataset that we will use in this blog is this dataset from Kaggle which contains 16240 upper clothes for women with 256*192 resolution.

Load all dependencies we need

As always let's start by loading all dependencies we need.

We first will import torch since we will use PyTorch, and from there we import nn. That will help us create and train the networks, and also let us import optim, a package that implements various optimization algorithms (e.g. sgd, adam,..). From torchvision we import datasets and transforms to prepare the data and apply some transforms.

We will import functional as F from torch.nn, DataLoader from torch.utils.data to create mini-batch sizes, save_image from torchvision.utils to save some fake samples, log2 and sqrt form math, Numpy for linear algebra, os for interaction with the operating system, tqdm to show progress bars, and finally matplotlib.pyplot to plot some images.

import torch
from torch import nn, optim
from torchvision import datasets, transforms
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision.utils import save_image
from math import log2, sqrt
import numpy as np
import os
from tqdm import tqdm
import matplotlib.pyplot as plt

Hyperparameters

Initialize the DATASET by the path of the real images.
Initialize the device by Cuda if it is available and CPU otherwise, the number of epochs by 300, the learning rate by 0.001, and the batch size by 32.
Initialize LOG_RESOLUTION by 7 because we are trying to generate 128*128 images, and 2^7 = 128. you can change the value depending on the resolution of the fake images that you want.
In the original paper, they initialize Z_DIM and W_DIM by 512, but I initialize them by 256 instead for less VRAM usage and speed-up training. We could perhaps even get better results if we doubled them.
For StyleGAN2 we can use any of the GANs loss functions we want, so I use WGAN-GP from the paper Improved Training of Wasserstein GANs. This loss contains a parameter name λ and it's common to set λ = 10.

DATASET                 = "Women clothes"
DEVICE                  = "cuda" if torch.cuda.is_available() else "cpu"
EPOCHS                  = 300
LEARNING_RATE           = 1e-3
BATCH_SIZE              = 32
LOG_RESOLUTION          = 7 #for 128*128
Z_DIM                   = 256
W_DIM                   = 256
LAMBDA_GP               = 10

Get data loader

Now let's create a function get_loader to:

Apply some transformation to the images (resize the images to the resolution that we want(2^LOG_RESOLUTION by 2^LOG_RESOLUTION), convert them to tensors, then apply some augmentation, and finally normalize them to be all the pixels ranging from -1 to 1).
Prepare the dataset by using ImageFolder because it's already structured in a nice way.
Create mini-batch sizes using DataLoader that take the dataset and batch size with shuffling the data.
Finally, return the loader.

def get_loader():
    transform = transforms.Compose(
        [
            transforms.Resize((2 ** LOG_RESOLUTION, 2 ** LOG_RESOLUTION)),
            transforms.ToTensor(),
            transforms.RandomHorizontalFlip(p=0.5),
            transforms.Normalize(
                [0.5, 0.5, 0.5],
                [0.5, 0.5, 0.5],
            ),
        ]
    )
    dataset = datasets.ImageFolder(root=DATASET, transform=transform)
    loader = DataLoader(
        dataset,
        batch_size=BATCH_SIZE,
        shuffle=True,
    )
    return loader

Models implementation

Now let's Implement the StyleGAN2 networks with the key attributions from the paper. We will try to make the implementation compact but also keep it readable and understandable. Specifically, the key points:

Noise Mapping Network
Weight demodulation (Instead of Adaptive Instance Normalization (AdaIN))
Skip connections (Instead of progressive growing)
Perceptual path length normalization

Noise Mapping Network

Let's create the MappingNetwork class which will be inherited from nn.Module.

In the init part we send z_dim and w_din, and we define the network mapping containing eight of EqualizedLinear, a class that we will implement later that equalizes the learning rate, and ReLu as an activation function
In the forward part, we initialize z_dim using pixel norm then we return the network mapping.

class MappingNetwork(nn.Module):
    def __init__(self, z_dim, w_dim):
        super().__init__()
        self.mapping = nn.Sequential(
            EqualizedLinear(z_dim, w_dim),
            nn.ReLU(),
            EqualizedLinear(z_dim, w_dim),
            nn.ReLU(),
            EqualizedLinear(z_dim, w_dim),
            nn.ReLU(),
            EqualizedLinear(z_dim, w_dim),
            nn.ReLU(),
            EqualizedLinear(z_dim, w_dim),
            nn.ReLU(),
            EqualizedLinear(z_dim, w_dim),
            nn.ReLU(),
            EqualizedLinear(z_dim, w_dim),
            nn.ReLU(),
            EqualizedLinear(z_dim, w_dim)
        )

    def forward(self, x):
    	  x = x / torch.sqrt(torch.mean(x ** 2, dim=1, keepdim=True) + 1e-8)  # for PixelNorm 
        return self.mapping(x)

Generator

In the figure below you can see the generator architecture where it starts with an initial constant. Then it has a series of blocks. The feature map resolution is doubled at each block. Each block outputs an RGB image and they are scaled up and summed to get the final RGB image.

toRGB also has a style modulation which is not shown in the figure to keep it simple.

To make the code as clean as possible, in the implementation of the generator we will use three classes that we will define later (StyleBlock, toRGB, and GeneratorBlock).

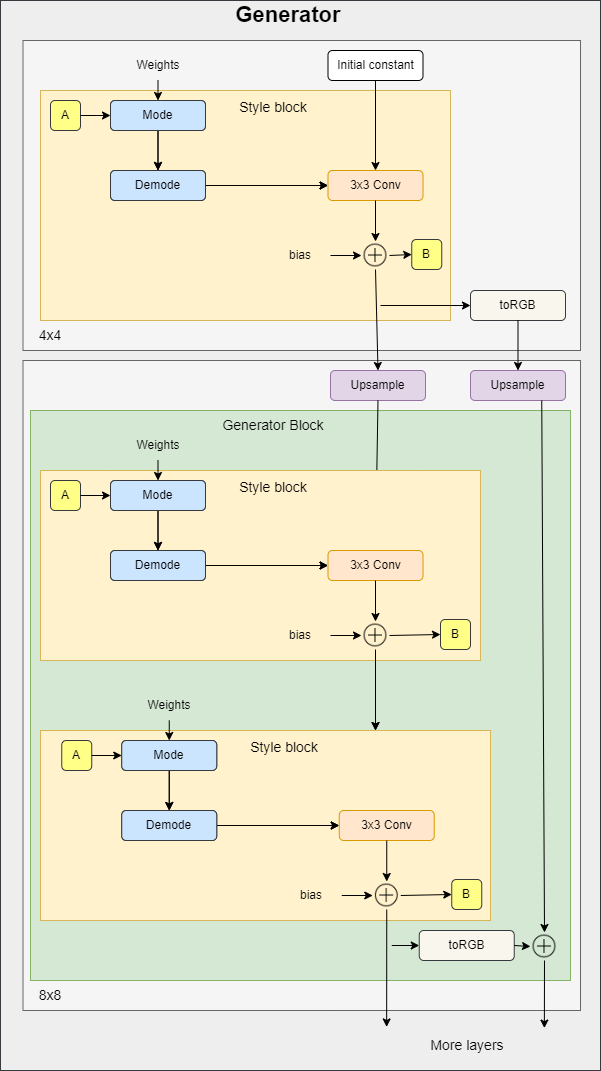
In the init part, we send log_resolution which is the log2 of image resolution, W_DIM which s the dimensionality of w, n_featurese which is the number of features in the convolution layer at the highest resolution (final block), max_features which is the maximum number of features in any generator block. We calculate the number of features for each block, we get the number of generator blocks, and we initialize the trainable 4x4 constant, the first style block for 4×4 resolution, the layer to get RGB, and the generator blocks.
In the forward part, we send in w for each generator block it has shape [n_blocks, batch_size, W-dim], and input_noise which is the noise for each block, it's a list of pairs of noise tensors because each block (except the initial) has two noise inputs after each convolution layer (see the figure above). We get the batch size, expand the learned constant to match the batch size, run it into the first style block, get the RGB image, then run it again into the rest of the generator blocks after upsampling. Finally, return the last RGB image with tanh as an activation function. The reason why we use tanh is that will be the output(the generated image) and we want the pixels to range between 1 and -1.

class Generator(nn.Module):

    def __init__(self, log_resolution, W_DIM, n_features = 32, max_features = 256):

        super().__init__()

        features = [min(max_features, n_features * (2 ** i)) for i in range(log_resolution - 2, -1, -1)]
        self.n_blocks = len(features)

        self.initial_constant = nn.Parameter(torch.randn((1, features[0], 4, 4)))

        self.style_block = StyleBlock(W_DIM, features[0], features[0])
        self.to_rgb = ToRGB(W_DIM, features[0])

        blocks = [GeneratorBlock(W_DIM, features[i - 1], features[i]) for i in range(1, self.n_blocks)]
        self.blocks = nn.ModuleList(blocks)

    def forward(self, w, input_noise):

        batch_size = w.shape[1]

        x = self.initial_constant.expand(batch_size, -1, -1, -1)
        x = self.style_block(x, w[0], input_noise[0][1])
        rgb = self.to_rgb(x, w[0])

        for i in range(1, self.n_blocks):
            x = F.interpolate(x, scale_factor=2, mode="bilinear")
            x, rgb_new = self.blocks[i - 1](x, w[i], input_noise[i])
            rgb = F.interpolate(rgb, scale_factor=2, mode="bilinear") + rgb_new

        return torch.tanh(rgb)

Generator Block

In the figure below you can see the generator block architecture which consists of two style blocks (3×3 convolutions with style modulation) and RGB output.

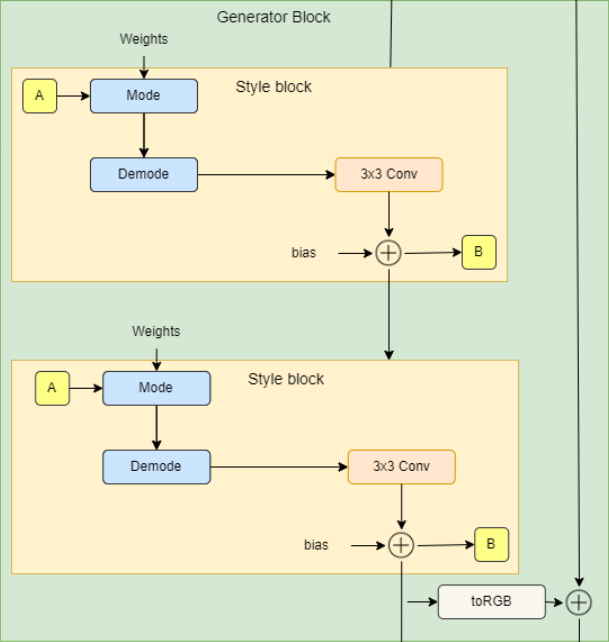
In the init part, we send in W_DIM which is the dimensionality of w, in_features which is the number of features in the input feature map, and out_features which is the number of features in the output feature map, then we initialize two style blocks and toRGB layer.
In the forward part, we send in x which is the input feature map of the shape [batch_size, in_features, height, width], w with the shape [batch_size, W_DIM], and noise which is a tuple of two noise tensors of shape [batch_size, 1, height, width], then we run x into the two style blocks and we get the RGB image using the layer toRGB. Finally, we return x and the RGB image.

class GeneratorBlock(nn.Module):

    def __init__(self, W_DIM, in_features, out_features):

        super().__init__()

        self.style_block1 = StyleBlock(W_DIM, in_features, out_features)
        self.style_block2 = StyleBlock(W_DIM, out_features, out_features)

        self.to_rgb = ToRGB(W_DIM, out_features)

    def forward(self, x, w, noise):

        x = self.style_block1(x, w, noise[0])
        x = self.style_block2(x, w, noise[1])

        rgb = self.to_rgb(x, w)

        return x, rgb

Style Block

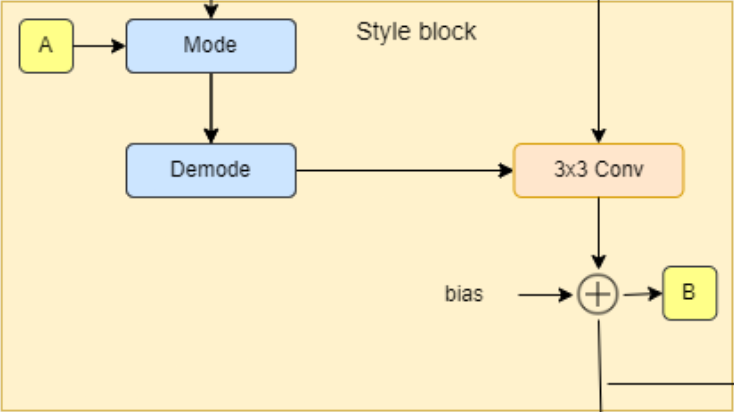
In the init part, we send W_DIM, in_features, and out_features, then we initialize to_style by the style vector that we get from w (denoted by A in the diagram) with an equalized learning rate linear layer (EqualizedLinear) that we will implement later, weight modulated convolution layer, noise scale, bias, and activation function.
In the forward part, we send x, w, and noise, then we get the style vector s, run x and s into the weight modulated convolution, scale and add noise, and finally add bias and evaluate the activation function.

class StyleBlock(nn.Module):

    def __init__(self, W_DIM, in_features, out_features):

        super().__init__()

        self.to_style = EqualizedLinear(W_DIM, in_features, bias=1.0)
        self.conv = Conv2dWeightModulate(in_features, out_features, kernel_size=3)
        self.scale_noise = nn.Parameter(torch.zeros(1))
        self.bias = nn.Parameter(torch.zeros(out_features))

        self.activation = nn.LeakyReLU(0.2, True)

    def forward(self, x, w, noise):

        s = self.to_style(w)
        x = self.conv(x, s)
        if noise is not None:
            x = x + self.scale_noise[None, :, None, None] * noise
        return self.activation(x + self.bias[None, :, None, None])

To RGB

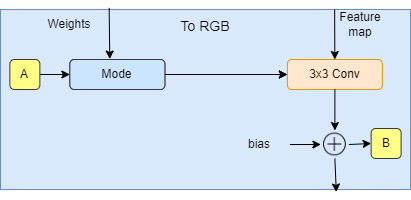
In the init part, we send W_DIM, and features, then we initialize to_style by the style vector that we get from w (denoted by A in the diagram), weight modulated convolution layer, bias, and activation function.
In the forward part, we send x, and w, then we get the style vector style, we run x and style into the weight modulated convolution, and finally, we add bias and evaluate the activation function.

class ToRGB(nn.Module):

    def __init__(self, W_DIM, features):

        super().__init__()
        self.to_style = EqualizedLinear(W_DIM, features, bias=1.0)

        self.conv = Conv2dWeightModulate(features, 3, kernel_size=1, demodulate=False)
        self.bias = nn.Parameter(torch.zeros(3))
        self.activation = nn.LeakyReLU(0.2, True)

    def forward(self, x, w):

        style = self.to_style(w)
        x = self.conv(x, style)
        return self.activation(x + self.bias[None, :, None, None])

Convolution with Weight Modulation and Demodulation

Bring this project to life

Run on Gradient

This class scales the convolution weights by the style vector and demodulates it by normalizing it.

In the init part, we send in_features, out_features, kernel_size, demodulates which is a flag whether to normalize weights by its standard deviation, and eps which is the ϵ for normalizing, then we initialize the number of output features, demodulate, padding size, Weights parameter with equalized learning rate using the class EqualizedWeight that we will implement later, and eps.
In the forward part, we send in x which is the input feature map, and s which is a style-based scaling tensor, then we get the batch size, height, and width from x, reshape the scales, get the learning rate equalized weights, then modulate x and s, and demodulate them if demodulates is True using the equations below where i is the input channel, j is the output channel, and k is the kernel index. And finally, we return x.

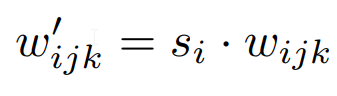
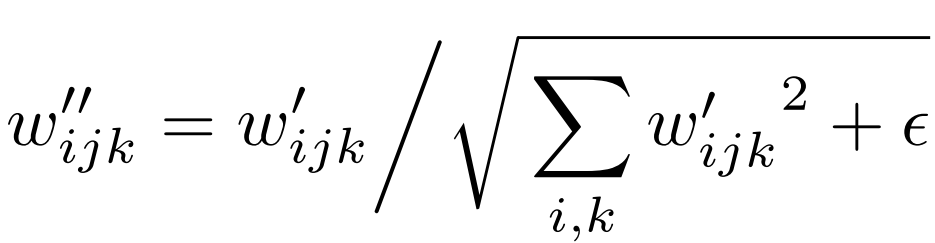
The equation for modulating. Image from the research paper

The equation for demodulating. Image from the research paper

class Conv2dWeightModulate(nn.Module):

    def __init__(self, in_features, out_features, kernel_size,
                 demodulate = True, eps = 1e-8):

        super().__init__()
        self.out_features = out_features
        self.demodulate = demodulate
        self.padding = (kernel_size - 1) // 2

        self.weight = EqualizedWeight([out_features, in_features, kernel_size, kernel_size])
        self.eps = eps

    def forward(self, x, s):

        b, _, h, w = x.shape

        s = s[:, None, :, None, None]
        weights = self.weight()[None, :, :, :, :]
        weights = weights * s

        if self.demodulate:
            sigma_inv = torch.rsqrt((weights ** 2).sum(dim=(2, 3, 4), keepdim=True) + self.eps)
            weights = weights * sigma_inv

        x = x.reshape(1, -1, h, w)

        _, _, *ws = weights.shape
        weights = weights.reshape(b * self.out_features, *ws)

        x = F.conv2d(x, weights, padding=self.padding, groups=b)

        return x.reshape(-1, self.out_features, h, w)

Discriminator

In the figure below you can see the discriminator architecture. It first transforms the image with the resolution 2^{LOG_RESOLUTION} by 2^{LOG_RESOLUTION} to a feature map of the same resolution and then runs it through a series of blocks with residual connections. The resolution is down-sampled by 2× at each block while doubling the number of features.

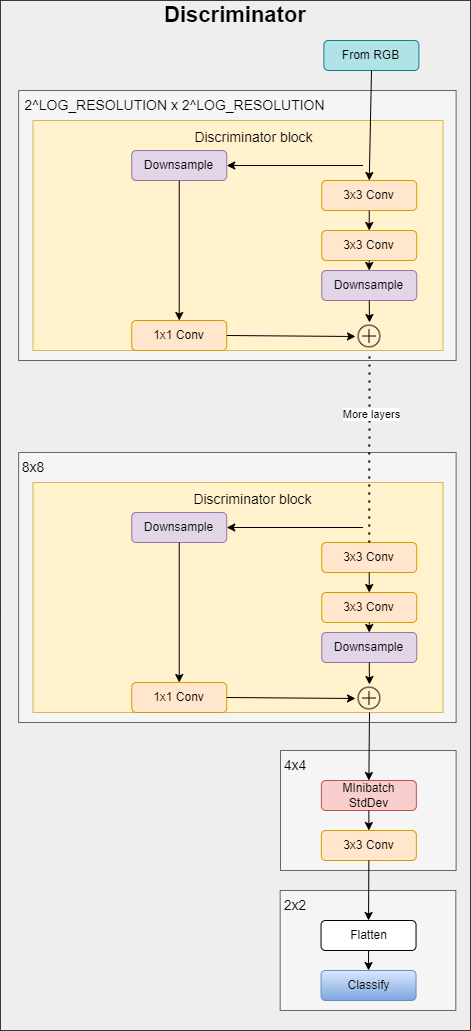
In the init part, we send in log_resolution, n_feautures, and max_features, calculate the number of features for each block, then initialize a layer with the name from_rgb to convert the RGB image to a feature map with n_features number of features, number of discriminator blocks, discriminator blocks, number of features after adding the map of the standard deviation, final 3×3 convolution layer, and final linear layer to get the classification.
For Minibatch std on Discriminator, we add the minibatch_std part when we take the std for each example (across all channels, and pixels) then we repeat it for a single channel and concatenate it with the image. In this way, the discriminator will get information about the variation in the batch/image.
In the forward part, we send in x which is the input image of the shape [batch_size, 3, height, width], and we run it throw the from_RGB layer, discriminator blocks, minibatch_std, 3×3 convolution, flatten, and classification score.

class Discriminator(nn.Module):

    def __init__(self, log_resolution, n_features = 64, max_features = 256):

        super().__init__()

        features = [min(max_features, n_features * (2 ** i)) for i in range(log_resolution - 1)]

        self.from_rgb = nn.Sequential(
            EqualizedConv2d(3, n_features, 1),
            nn.LeakyReLU(0.2, True),
        )
        n_blocks = len(features) - 1
        blocks = [DiscriminatorBlock(features[i], features[i + 1]) for i in range(n_blocks)]
        self.blocks = nn.Sequential(*blocks)

        final_features = features[-1] + 1
        self.conv = EqualizedConv2d(final_features, final_features, 3)
        self.final = EqualizedLinear(2 * 2 * final_features, 1)

    def minibatch_std(self, x):
        batch_statistics = (
            torch.std(x, dim=0).mean().repeat(x.shape[0], 1, x.shape[2], x.shape[3])
        )
        return torch.cat([x, batch_statistics], dim=1)

    def forward(self, x):

        x = self.from_rgb(x)
        x = self.blocks(x)

        x = self.minibatch_std(x)
        x = self.conv(x)
        x = x.reshape(x.shape[0], -1)
        return self.final(x)

Discriminator Block

In the figure below you can see the discriminator block architecture that consists of two 3×3 convolutions with a residual connection.

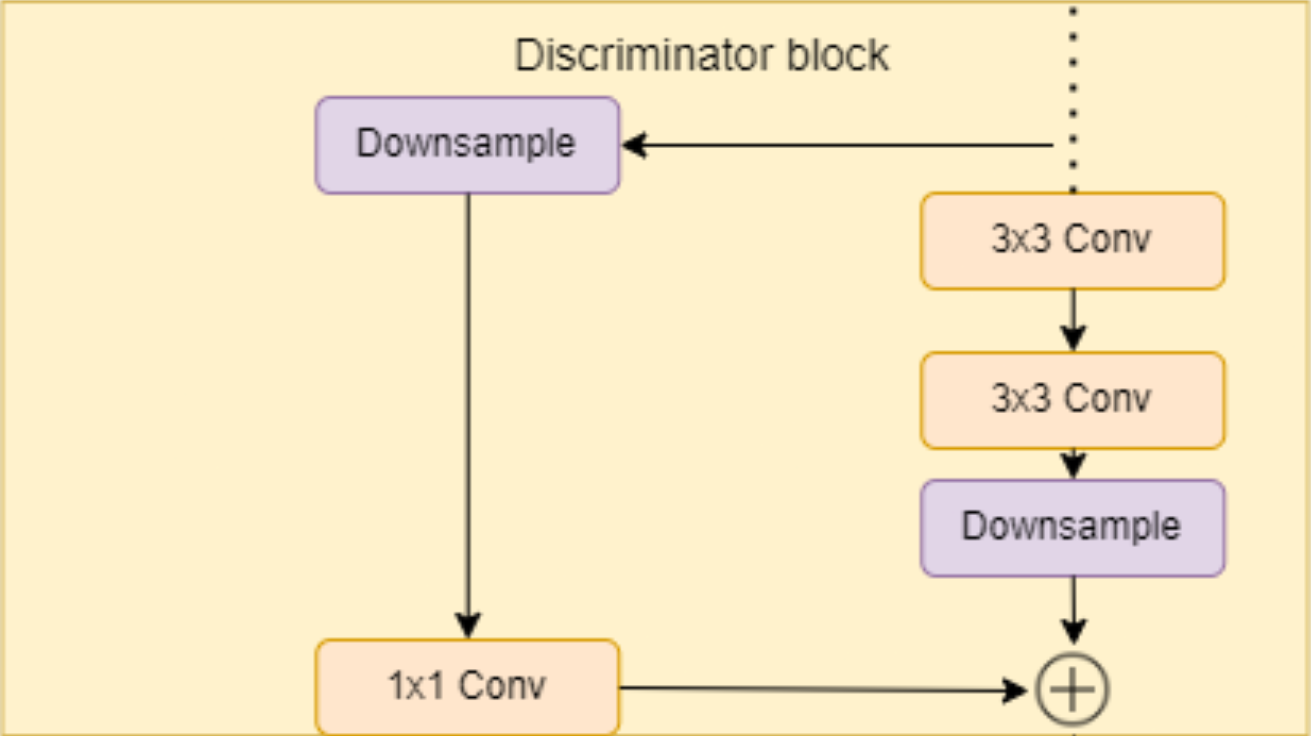
In the init part, we send in in_features and out_features, and we initialize the residual block that contains down-sampling and a 1×1 convolution layer for the residual connection, the block layer that contains two 3×3 convolutions with Leaky Rely as activation function, down_sample layer using AvgPool2d, and the scale factor that we will use after adding the residual.
In the forward part, we send in x and we run it throw the residual connection to get a variable with the name residual, then we run x throw the convolutions and downsample, then we add the residual and scale, and we return it.

class DiscriminatorBlock(nn.Module):

    def __init__(self, in_features, out_features):
        super().__init__()
        self.residual = nn.Sequential(nn.AvgPool2d(kernel_size=2, stride=2), # down sampling using avg pool
                                      EqualizedConv2d(in_features, out_features, kernel_size=1))

        self.block = nn.Sequential(
            EqualizedConv2d(in_features, in_features, kernel_size=3, padding=1),
            nn.LeakyReLU(0.2, True),
            EqualizedConv2d(in_features, out_features, kernel_size=3, padding=1),
            nn.LeakyReLU(0.2, True),
        )

        self.down_sample = nn.AvgPool2d(
            kernel_size=2, stride=2
        )  # down sampling using avg pool

        self.scale = 1 / sqrt(2)

    def forward(self, x):
        residual = self.residual(x)

        x = self.block(x)
        x = self.down_sample(x)

        return (x + residual) * self.scale

Learning-rate Equalized Linear Layer

Now it is time to implement EqualizedLinear that we use earlier in almost every class to equalize the learning rate for a linear layer.

In the init part, we send in in_features, out_features, and bias. We initialize the weight by a class EqualizedWeight that we will define later, and we initialize the bias.
In the forward part, we send in x and return the linear transformation of x, weight, and bias

class EqualizedLinear(nn.Module):

    def __init__(self, in_features, out_features, bias = 0.):

        super().__init__()
        self.weight = EqualizedWeight([out_features, in_features])
        self.bias = nn.Parameter(torch.ones(out_features) * bias)

    def forward(self, x: torch.Tensor):
        return F.linear(x, self.weight(), bias=self.bias)

Learning-rate Equalized 2D Convolution Layer

Now let's implement EqualizedConv2d that we use earlier to equalize the learning rate for a convolution layer.

In the init part, we send in in_features, out_features, kernel_size, and padding. We initialize the padding, the weight by a class EqualizedWeight that we will define later, and the bias.
In the forward part, we send in x and return the convolution of x, weight, bias, and padding.

class EqualizedConv2d(nn.Module):

    def __init__(self, in_features, out_features,
                 kernel_size, padding = 0):

        super().__init__()
        self.padding = padding
        self.weight = EqualizedWeight([out_features, in_features, kernel_size, kernel_size])
        self.bias = nn.Parameter(torch.ones(out_features))

    def forward(self, x: torch.Tensor):
        return F.conv2d(x, self.weight(), bias=self.bias, padding=self.padding)

Learning-rate Equalized Weights Parameter

Now let's implement EqualizedWeight class that we use in Learning-rate Equalized Linear Layer and Learning-rate Equalized 2D Convolution Layer.

This is based on equalized learning rate introduced in the ProGAN paper. Instead of initializing weights at N(0,c) they initialize weights to N(0,1) and then multiply them by c when using it.

In the init part, we send in the shape of the weight parameter, we initialize the constant c and the weights with N(0,1).
In the forward part, we multiply weights by c and return.

class EqualizedWeight(nn.Module):

    def __init__(self, shape):

        super().__init__()

        self.c = 1 / sqrt(np.prod(shape[1:]))
        self.weight = nn.Parameter(torch.randn(shape))

    def forward(self):
        return self.weight * self.c

Perceptual path length normalization

Perceptual path length normalization encourages a fixed-size step in w to result in a fixed-magnitude change in the image.

Where Jw is calculated with the equation below, w is sampled from the mapping network, y are images with noise N(0, I), and a is the exponential moving average as the training progresses.

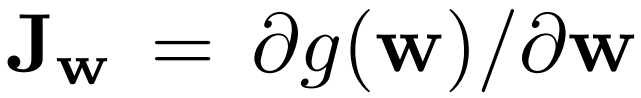
In the init part, we send in beta which is the constant β used to calculate the exponential moving average a. Initialize beta, steps by the number of steps calculated N, exp_sum_a by the exponential sum of J_w^Ty.
In the forward part, we send in x which is the batch of w of shape [batch_size, W_DIM] and x are the generated images of shape [batch_size, 3, height, width], get the device and number of pixels, calculate the equations above, update exponential sum, increment N, and return the penalty.

class PathLengthPenalty(nn.Module):

    def __init__(self, beta):

        super().__init__()

        self.beta = beta
        self.steps = nn.Parameter(torch.tensor(0.), requires_grad=False)

        self.exp_sum_a = nn.Parameter(torch.tensor(0.), requires_grad=False)

    def forward(self, w, x):

        device = x.device
        image_size = x.shape[2] * x.shape[3]
        y = torch.randn(x.shape, device=device)

        output = (x * y).sum() / sqrt(image_size)
        sqrt(image_size)

        gradients, *_ = torch.autograd.grad(outputs=output,
                                            inputs=w,
                                            grad_outputs=torch.ones(output.shape, device=device),
                                            create_graph=True)

        norm = (gradients ** 2).sum(dim=2).mean(dim=1).sqrt()

        if self.steps > 0:

            a = self.exp_sum_a / (1 - self.beta ** self.steps)

            loss = torch.mean((norm - a) ** 2)
        else:
            loss = norm.new_tensor(0)

        mean = norm.mean().detach()
        self.exp_sum_a.mul_(self.beta).add_(mean, alpha=1 - self.beta)
        self.steps.add_(1.)

        return loss

Utils

gradient_penalty

In the code snippet below you can find the gradient_penalty function for WGAN-GP loss.

def gradient_penalty(critic, real, fake,device="cpu"):
    BATCH_SIZE, C, H, W = real.shape
    beta = torch.rand((BATCH_SIZE, 1, 1, 1)).repeat(1, C, H, W).to(device)
    interpolated_images = real * beta + fake.detach() * (1 - beta)
    interpolated_images.requires_grad_(True)

    # Calculate critic scores
    mixed_scores = critic(interpolated_images)
 
    # Take the gradient of the scores with respect to the images
    gradient = torch.autograd.grad(
        inputs=interpolated_images,
        outputs=mixed_scores,
        grad_outputs=torch.ones_like(mixed_scores),
        create_graph=True,
        retain_graph=True,
    )[0]
    gradient = gradient.view(gradient.shape[0], -1)
    gradient_norm = gradient.norm(2, dim=1)
    gradient_penalty = torch.mean((gradient_norm - 1) ** 2)
    return gradient_penalty

Sample W

This function samples Z randomly and gets W from the mapping network.

def get_w(batch_size):

    z = torch.randn(batch_size, W_DIM).to(DEVICE)
    w = mapping_network(z)
    return w[None, :, :].expand(LOG_RESOLUTION, -1, -1)

Generate noise

This function generates noise for each generator block

def get_noise(batch_size):
    
        noise = []
        resolution = 4

        for i in range(LOG_RESOLUTION):
            if i == 0:
                n1 = None
            else:
                n1 = torch.randn(batch_size, 1, resolution, resolution, device=DEVICE)
            n2 = torch.randn(batch_size, 1, resolution, resolution, device=DEVICE)

            noise.append((n1, n2))

            resolution *= 2

        return noise

In the code snippet below you can find the generate_examples function that takes the generator gen, the number of epochs, and a number n=100. The goal of this function is to generate n fake images and save them as a result for each epoch.

def generate_examples(gen, epoch, n=100):
    
    gen.eval()
    alpha = 1.0
    for i in range(n):
        with torch.no_grad():
            w     = get_w(1)
            noise = get_noise(1)
            img = gen(w, noise)
            if not os.path.exists(f'saved_examples/epoch{epoch}'):
                os.makedirs(f'saved_examples/epoch{epoch}')
            save_image(img*0.5+0.5, f"saved_examples/epoch{epoch}/img_{i}.png")

    gen.train()

Training

In this section, we will train our StyleGAN2.

Let's start by creating the train function that takes the discriminator/critic, gen for generator, path_length_penalty that we will use every 16 epochs, loader, and the optimizers for the networks. We start by looping over all the mini-batch sizes that we create with the DataLoader, and we take just the images because we don't need a label.

Then we set up the training for the discriminator\Critic when we want to maximize E(critic(real)) - E(critic(fake)). This equation means how much the critic can distinguish between real and fake images.

After that, we set up the training for the generator and mapping network when we want to maximize E(critic(fake)), and we add to this function a perceptual path length every 16 epochs.

Finally, we update the loop.

def train_fn(
    critic,
    gen,
    path_length_penalty,
    loader,
    opt_critic,
    opt_gen,
    opt_mapping_network,
):
    loop = tqdm(loader, leave=True)

    for batch_idx, (real, _) in enumerate(loop):
        real = real.to(DEVICE)
        cur_batch_size = real.shape[0]

        w     = get_w(cur_batch_size)
        noise = get_noise(cur_batch_size)
        with torch.cuda.amp.autocast():
            fake = gen(w, noise)
            critic_fake = critic(fake.detach())
            
            critic_real = critic(real)
            gp = gradient_penalty(critic, real, fake, device=DEVICE)
            loss_critic = (
                -(torch.mean(critic_real) - torch.mean(critic_fake))
                + LAMBDA_GP * gp
                + (0.001 * torch.mean(critic_real ** 2))
            )

        critic.zero_grad()
        loss_critic.backward()
        opt_critic.step()

        gen_fake = critic(fake)
        loss_gen = -torch.mean(gen_fake)

        if batch_idx % 16 == 0:
            plp = path_length_penalty(w, fake)
            if not torch.isnan(plp):
                loss_gen = loss_gen + plp

        mapping_network.zero_grad()
        gen.zero_grad()
        loss_gen.backward()
        opt_gen.step()
        opt_mapping_network.step()

        loop.set_postfix(
            gp=gp.item(),
            loss_critic=loss_critic.item(),
        )

Now let's initialize the loader, the networks, and the optimizers, and make the networks in the training mode

loader              = get_loader()

gen                 = Generator(LOG_RESOLUTION, W_DIM).to(DEVICE)
critic              = Discriminator(LOG_RESOLUTION).to(DEVICE)
mapping_network     = MappingNetwork(Z_DIM, W_DIM).to(DEVICE)
path_length_penalty = PathLengthPenalty(0.99).to(DEVICE)

opt_gen             = optim.Adam(gen.parameters(), lr=LEARNING_RATE, betas=(0.0, 0.99))
opt_critic          = optim.Adam(critic.parameters(), lr=LEARNING_RATE, betas=(0.0, 0.99))
opt_mapping_network = optim.Adam(mapping_network.parameters(), lr=LEARNING_RATE, betas=(0.0, 0.99))

gen.train()
critic.train()
mapping_network.train()

Now let's train the networks using the training loop, and save some fake samples in each 50 epoch.

loader = get_loader()  

for epoch in range(EPOCHS):
    train_fn(
        critic,
        gen,
        path_length_penalty,
        loader,
        opt_critic,
        opt_gen,
        opt_mapping_network,
    )
    if epoch % 50 == 0:
    	generate_examples(gen, epoch)

Conclusion

In this article, we make a clean, simple, and readable implementation from scratch for a huge project which is StyleGAN2 using PyTorch. we try to replicate the original paper as closely as possible.

Add speed and simplicity to your Machine Learning workflow today

Get started

Blog

Docs

Community

ML Showcase

Professional Services

Talk to an Expert

Understanding StyleGAN2

Large Language Models: Fine-tuning MPT-7B on Paperspace

Solutions

Product

Resources

Company