Geometric Deep Learning Library Comparison

In our last post introducing Geometric Deep Learning we situated the topic within the context of the current Deep Learning gold rush. Critically, we outlined what makes GDL stand out in terms of its potential. For this post, it is sufficient to know that GDL is deep learning performed on irregular data structures, such as graphs, meshes, and point clouds.

We also showed relevant tasks on which state-of-the-art performance can be achieved by employing GDL approaches. Despite performing well on various tasks, the irregular data structures in GDL cannot be fit easily into existing Deep Learning frameworks. This poor fit necessitates the development of new libraries for effective and efficient computation. We'll briefly introduce some relevant details on how libraries for GDL model this irregular data and computations on it, focusing on what consequences this has for the end-user.

Finally, as promised in the post's title, we'll briefly discuss and compare each of the current main libraries for GDL. The comparison is performed by way of a morphological analysis based on an exemplary use-case. We provide the tools used for this analysis, and you can easily customize them to your use-case and requirements. In the end we'll discuss some of the key differences between the libraries, and conclude with advice on which library to use for three typical use-cases: scientific research, production-level development, and casual hobby.

The sections are as follows:

• Implementation Details
• PyTorch Geometric
• Deep Graph Library
• Graph Nets
• Morphological Analysis
• Honorable Mentions
• Key Differences
• Which One Should I Choose?

Introduction

Among the many innovations sparked by advances in Deep Learning was the creation of software development frameworks specific for this field. The list of frameworks and libraries is extensive, and the primary focus they have varies, but there are still commonalities between them. Most offer a basic set of layers and functions with support for multi-threading on the CPU and offloading of parallel computations to the GPU, while relying on automatic differentiation for quickly computing gradients for backpropagation.

But to what extent have Deep Learning frameworks permeated software development processes? To answer this question, we need a proxy for the relevancy of these frameworks. As it is commonplace for software developers, irrespective of their background, to use search engines to aid in gathering information before and during projects, we'll use Google Trends as a proxy for relevancy. We compared search terms to search topics, so bear in mind that there are more terms hidden within the latter (e.g. for C-programming language). The values in the graphs below are normalized web searches for a better comparison between different topics, and are aggregated worldwide. It is evident from the chart that there is substantial interest, even more so if one takes into account that we're comparing frameworks with a general-purpose programming language.

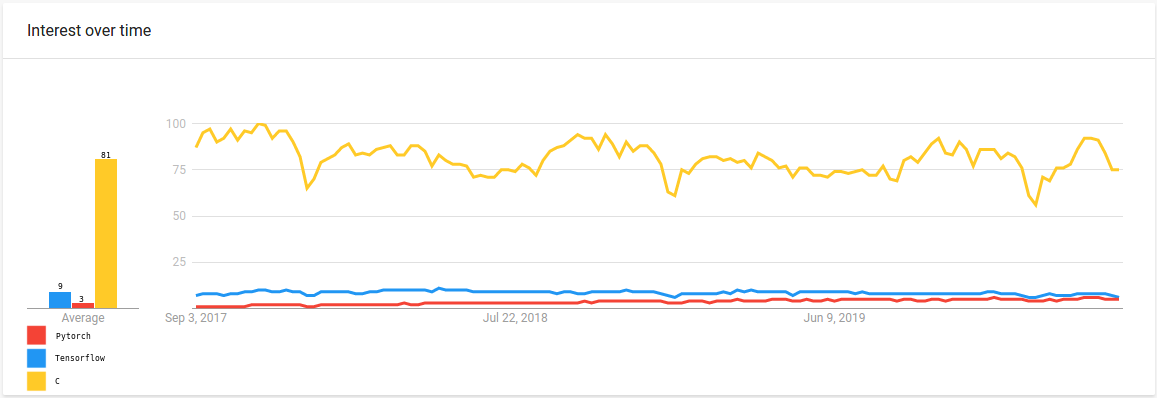
Interestingly, when closing in on specific countries for the previous query, this picture changes quite a bit. In China, the frameworks above even gain the upper hand, as can be seen below.

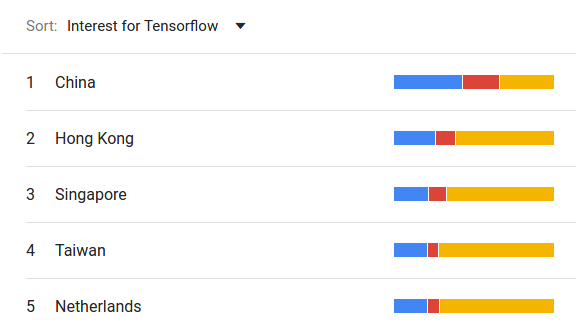
As Baidu has a far larger market share in China, and these results only pertain to Google web searches, we have to take this data with a grain of salt. Furthermore, there are alternative, equally valuable proxies, e.g. survey data from StackOverflow or GitHub public repository data. The advantage of Web Search data is that it is quite close to an unbiased view of what interests people. A survey has a plethora of biases that have to be taken into account when interpreting the data. Regarding GitHub, relying only on public data skews our view as this will only contain open-source projects, which only constitute a fraction of the whole picture.

How do GDL libraries fare in the context of deep learning frameworks?

From the charts above, it is quite apparent that GDL libraries are still in a tiny niche of early adoption within the Deep Learning community, as evidenced by the periods with close to no web searches. In the comparison graph with TensorFlow their web searches barely make a dent. Regarding interest between the single GDL libraries, there's a definite uptick in competition and overall interest values from the beginning of 2019. There's also a slightly more maintained rate of interest from May 2019. This change of pace is no coincidence, as both PyTorch Geometric and the Deep Graph Library were officially presented in workshops on that occasion, accompanied by workshop paper publications.

Taking the Google Trends information into consideration, why bother with GDL?

Well, do you want to be the 100,000th person to perform neural style transform, or be at the forefront of Deep Learning development? If you responded affirmatively to the latter, read on.

GDL Libraries

Bronstein et al. mention computational frameworks for GDL as one of the future needs in the GDL field in their seminal work from 2017. [3]

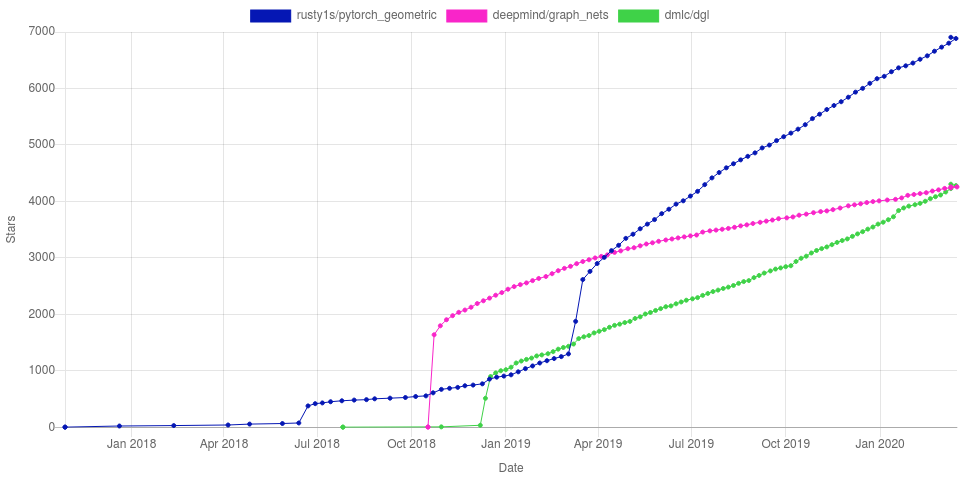
As can be seen in the graph below, the libraries which this post revolves around were developed soon afterwards. The naming of PyTorch Geometric also highlights the impact of the article.

There are two things which are important to note here:

• Recency: These libraries have been in development for a bit over two years; this is nothing for a field that is equally young.
• Popularity: PyTorch Geometric already has a fifth of the GitHub stars amassed by its parent framework PyTorch. Does this contradict our Google Trends results? Not at all, there might be a large community of early adopters.

In the following sections we'll briefly touch on the implementation details of these libraries, summarize each, perform an exemplary morphological analysis, and provide you with the tools necessary to perform one for your particular use-case.

Implementation Details

Current frameworks are optimized for running algorithms on euclidean, grid-like data, accelerating these operations by using GPUs or other specific hardware. One of the existing approaches is to try to fit the graph-like data into data structures that conform to the current optimized operations, like Conv2D. In "MeshCNN: a network with an edge," for example, Hanocka et al. convert the meshes and the features they use into tensors to be able to use PyTorch's normal operations. [7]
This method, of course, incurs a cost for the overhead in data wrangling and doesn't guarantee optimal performance. Furthermore, by trying to comply with the requirements of tools that weren't developed for these data structures, one can miss out on innovative improvements. The global graph attribute introduced by Battaglia et al., which for a graph representing a multi-body mechanical system might be the gravitational field, is an excellent example of this.

Message Passing Scheme

One common attribute across all libraries mentioned in this comparison is that they rely on a message-passing scheme (as introduced by Gilmer et al.) to perform convolutions and other operations on graphs. [2] For an in-depth look at what precisely this means, Battaglia et al. and Fey et al. provide detailed explanations which I recommend you check out. [1][4] Furthermore, for those of you that learn better by example, here is a thorough explanation of how this scheme works in practice with a knowledge graph.

Regarding the implementation details of these libraries, there is one more important thing to note in this context. Gather scatter operations on the GPU are used to speed up methods following the message passing scheme interface. Inherently it comes with some disadvantages under the technical implementation. Usually, when performing experiments with stochastic processes, it is a best practice to set a seed for the random number generator to guarantee reproducibility of results while development is undergoing, or when testing experiments performed by others. Among other things, this ensures weights are initialized the same for each training iteration. More importantly, it also means that different training sessions with the same manual seed using the same specific architecture, set of hyperparameters, and dataset will always return the same results.

Fey et al. put this in the context of gather scatter operations in their workshop paper introducing their extension library:

In addition, it should be noted that scatter operations are non-deterministic by nature on the GPU. Although we did not observe any deviations for inference, training results can vary across the same manual seeds.

PyTorch Geometric

PyTorch Geometric is an extension library for PyTorch that makes it possible to perform usual deep learning tasks on non-euclidean data. The "Geometric" in its name is a reference to the definition for the field coined by Bronstein et al. [4][3]
Why is it an extension library and not a framework? Well, it fits perfectly into the PyTorch API, simply extending and improving its functionality for new use-cases.

It originated from research at the TU Dortmund and is mainly developed by Matthias Fey, a doctoral student who, in addition to developing this library, has developed SOTA approaches in this area. [4][6]

This proximity to Scientific Research shows in a large number of example implementations for recent research, as well as benchmark datasets for rapid prototyping or reproduction of results. Furthermore, since the beginning of April '19, it has been part of the official PyTorch Ecosystem and has a prominent place on the main project's landing page. This change can be seen in the previous GitHub stars history chart by a marked increase of its slope.

Graph Nets

Graph Nets is also an extension library. Developed as an internal project by the DeepMind team, it was open-sourced together with the publishing of the Battaglia et al. paper on the subject. [1]

Although it fits in nicely with the TensorFlow API, it depends on DeepMind's Sonnet, which makes its incorporation into TensorFlow's Ecosystem (like PyTorch Geometric) unlikely. Furthermore, despite being open-source, it is developed internally with infrequent updates to the public repository. There are clear signs, though, that development is steadily continuing privately by the example of the update for TensorFlow 2.0.

Deep Graph Library

This library doesn't extend any of the pre-existing frameworks for deep learning. Instead, it follows the API and paradigms of NetworkX closely in its architectural design, and offers a backend-agnostic library. [5]

Think of it as Keras for deep learning on graphs, where you have one set of API functions that can use different backend frameworks. It originates from research at NYU and AWS both in the US and Shanghai under the supervision of Yann LeCun, and is continually developed in cooperation. The team of current active contributors consists of around 12 people, and the project leads for NYU and AWS respectively are Minjie Wang and Da Zheng (information retrieved from the official GitHub repository public statistics and DGL's about page).

In the current stable version, v0.4.1, both PyTorch and MxNet are offered as backend frameworks, while TensorFlow support is still experimental. With the forthcoming release v0.5.0, TensorFlow will be incorporated into the stable version.

Morphological Analysis

We'll heavily rely on the DesignWIKI by Fil Salustri in this section and refer to relevant articles for a more detailed explanation of the process and background theory. Furthermore, for this section, I'll be performing the analysis from the point-of-view of a hobby developer. There will be additional pointers at the end of this section on how you can adjust the analysis to your use-case and what would probably change for Industrial or Scientific use.

What we want is a set of rules, which quickly and reliably leads us to the best library or framework for our use-case. It would be even better if you have a set of requirements to make the whole process more formal and your results a tad bit more reproducible.

Since the things we're comparing are very complicated and there are no apparent measures we can use to compare them to each other, we'll want to break the task of choosing between them down to small steps. Those familiar with algorithm design will see the familiarity to the Divide & Conquer paradigm. Luckily we can achieve our goal by using a simple approach called Weighted Decision Matrix (WDM). From the introduction of the aforelinked wiki entry: "A weighted decision matrix is a tool used to compare alternatives wrt multiple criteria of different levels of importance."

Perfect, this sounds exactly like what we're searching for. The first step is to define the criteria to compare the alternatives.

For my use-case, I've set the criteria to be the following:

• Performance: How many training iterations can we get in per time frame?
• Gap to Production: How easy is it to serve trained models, and is the necessary infrastructure for that available?
• Amount of Examples: How many examples of applications are there to get started?
• Popularity: Is there significant interest in the greater community?
• Roadmap: Are plans for future developments communicated clearly and publicly?
• Development Trend: Is there continuous development, and are there active maintainers?
• Framework Overhead: How much time do I have to invest in learning to use the extension library?

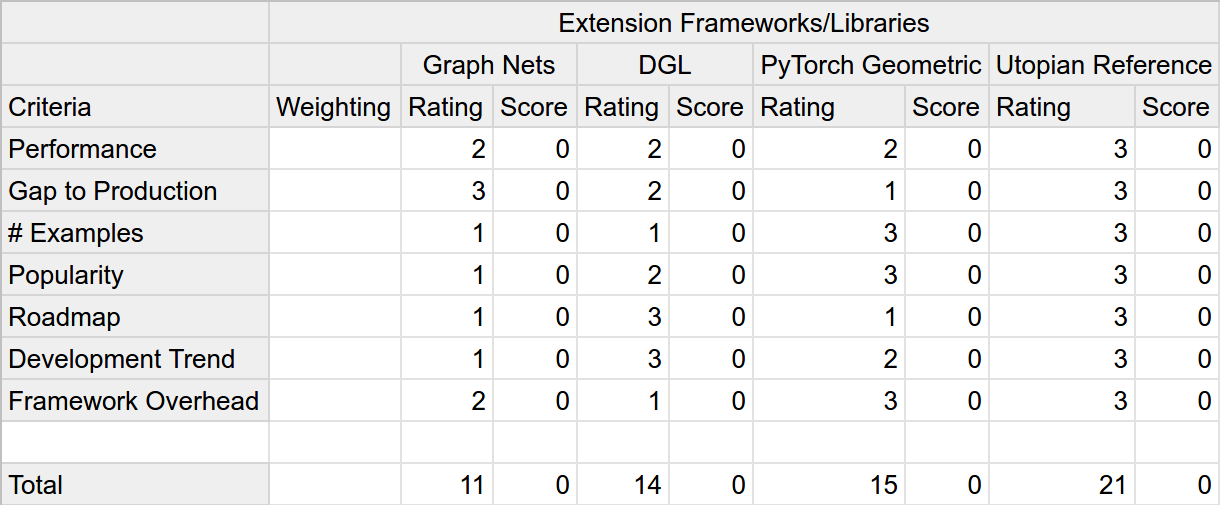
The next step is to create the WDM and fill in the scores for each one of our alternatives for the criteria we have chosen to use. Why don't we first calculate the relative importance of each criterion? Well, this way, we can shield ourselves from being biased against the less critical criteria's influence. Otherwise, we would tend to not think too hard about them and possibly come to wrong conclusions. For scoring each criterion, a Likert Scale usually is the recommended choice. In our example, the scores were relative, and the possible scores {1,2,3} can be interpreted as a ranking with one peculiarity: second place may remain unoccupied if the gap is large enough.

Upon rating each of our alternatives for the example scenario, this is the resulting matrix.

After this step, we need to set the relative importance level for each of the criteria, which in this instance, we'll do by performing a Pairwise Comparison. As with the WDM, we'll break a large and complex task into a bunch of small and simple ones. This part is also the point at which your own experience and knowledge come into play. Taking into consideration our requirements, for each unique combination of criteria, we will decide which one is more important for us and document this decision. We'll perform this comparison by using a spreadsheet application. The image below is the result of the example we're going through.
Note that whenever two letters are in the same cell, that means both criteria are equally important. Furthermore, the empty cells result in leaving out irrelevant information. We are not interested in comparing a criterion to itself or non-unique comparisons.

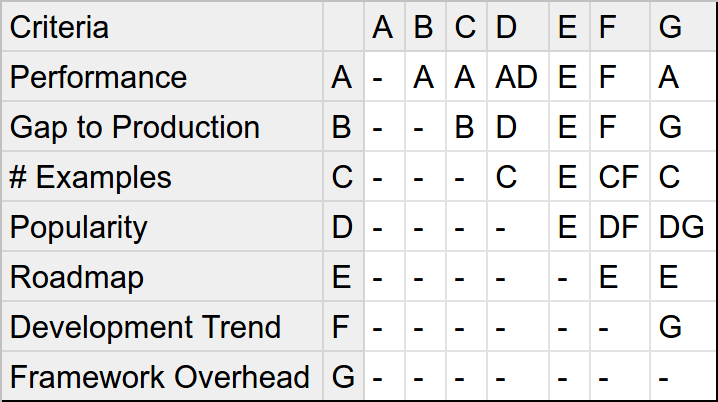
Now we simply tally up the amount of times each character appears in the table.
For the current example, this leads us to the following results.

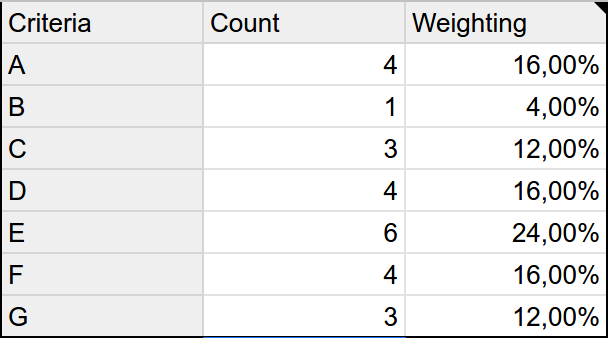
To calculate weightings for our criteria, we'll solve a simple linear equation based on the counts as follows:

From this equation, it follows that x = 4% which we can, in turn, multiply with each criterion's count to get its weighting.
In the Google Spreadsheet, everything is prepared for you to be able to play with these numbers. The formulae are also easy to adjust to your needs.

Now we can plug the weightings into the already prepared WDM and see if it changes our results in any way.

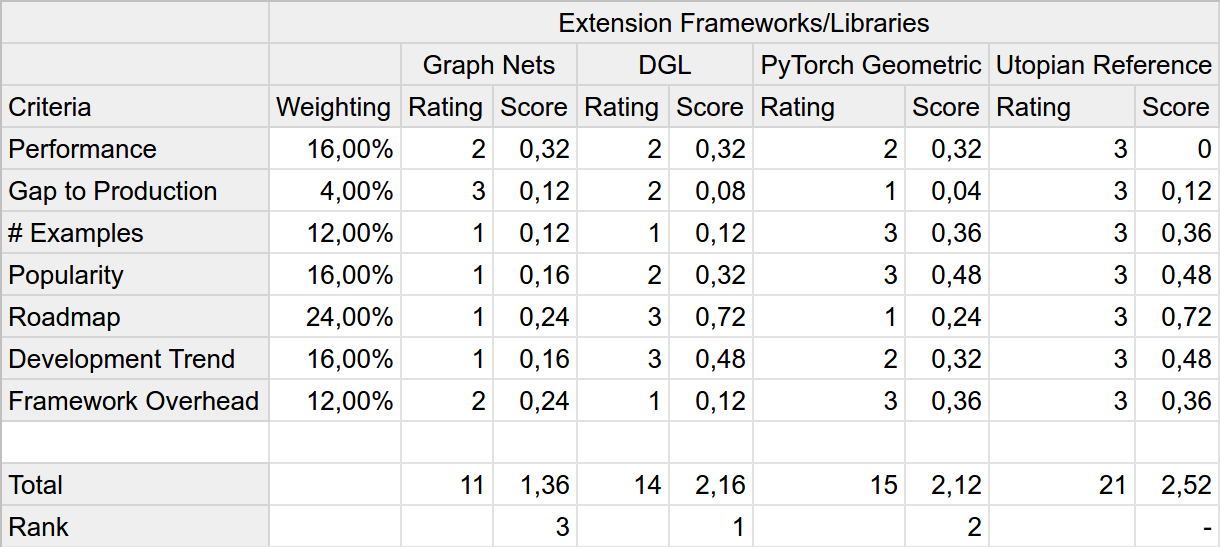
It does! Interestingly including the weighting of our scores increases the gap between Graph Nets and the other alternatives by a large margin. This increase is a direct result of it excelling at criteria that aren't that important in this example scenario, like the gap to production.

On the other hand, validating the chosen sequence of steps for calculating the WDM and minimizing bias, it is also the gap to production that separates our winner from the runner-up. Had we scored the alternatives after already calculating the weightings, we probably would've come to a different conclusion.

Recapitulating, to create the WDM we:

1. Defined a set of relevant and well-defined criteria
2. Scored each alternative on these criteria by using a relative ranking scale
3. Calculated the weighting of each criterion by using a pairwise comparison
4. Calculated the end score for each alternative

Furthermore, the criteria you choose should be as close to independent from each other as possible. Most important of all, don't give in to doing the procedure in a different order or change weightings after computing the total scores. By performing the process the correct way, we are minimizing the bias in our decision, which is of the utmost importance. To complete the analysis for your use-case, feel free to copy the Morphological Analysis Google Spreadsheet through the Google Sheets context menu: File -> Make a Copy

There are some caveats on the data used for the analysis in order of the affected criterion. The original post on performing a WDM from Fil Salustri's Design Site relied on a real reference alternative. In our take, this reference was utopian and served as an upper bound of what a perfect alternative would look like.
What would also be possible and fit in very nicely within this approach would be to use a baseline alternative. For GDL, this could represent your solution, trying to fit non-euclidean data into existing data structures and using the usual deep learning frameworks without any extensions. This way, the analysis would help you gauge if the additional overhead would be worth it - it probably is.

We did not perform any benchmarks ourselves, instead of relying on published literature regarding the alternatives. For this reason, we assume the performance as being approximately equal for the hobbyist scenario in this analysis, as the only available results, to my knowledge, are a comparison between DGL and PyTorch Geometric. [4][5]
If you have time to spare, definitely perform some benchmarks of your own. A useful resource for this would be the list of external sources listed on the PyTorch Geometric documentation.

There are alternatives for serving models for PyTorch, yet these come with additional costs compared to Tensorflow, hence the points for Graph Nets. Most often than not, models can be included in code for inference without any further features needed. For more complex serving scenarios, it is possible to convert PyTorch models to be used with Tensorflow Serving by using ONNX to convert them. Finally, MLFlow is a backend-agnostic alternative that is used to "... manage the ML lifecycle, including experimentation, reproducibility, and deployment."

The attentive reader might also have noticed that there are some slight inconsistencies in the analysis. If we take a closer look at the pairwise comparison we performed, there's a paradoxical connection between some of the decisions we took. According to our comparisons: G > B > C > G. This cannot be true. In other words, if the framework overhead is more important than the gap to production, which in turn is more important than the number of examples, which itself is more important than the framework overhead, then we don't have a total order. This error is also mentioned in the original post by Fil Salustri and is called the Arrow's Paradox.

Finally, some additional criteria that you could include or exchange with already included ones.

• Dataset Integration: How easy is it to import and work with benchmark datasets for specific tasks?
• Single Point of (Development) Failure: How would the library's development be affected if the lead developer suddenly left?

The former is very useful for overall benchmarking and especially for scientific research when developing new methods and needing to evaluate against the state-of-the-art. PyTorch Geometric lends itself very well to this as it both offers various implementations of methods from papers in the field and has by far the best integration with standard datasets.
The latter might be a make-or-break criterion for Industrial applications that need an open-source solution that is dependable. If the development team behind a project is too top-heavy, one key person leaving might lead to a significant gap in development and, in the worst-case scenario, to it stopping altogether. This risk often cannot be taken in situations where continuous development and delivery is a necessity.

Honorable Mentions

Mainly for Chinese readers:
Euler is an extension framework, similar to DGL, that uses TensorFlow or X-DeepLearning (Alibaba) as a backend. According to the documentation, PyTorch support is on its roadmap, potentially putting it in the run against DGL, at least for the Chinese market. Although the code and documentation are in English, communication on Issues and Pull Requests is in Chinese, which makes it a hard sell for non-Chinese speakers.
NeuGraph is a further framework developed in China by researchers from Peking University and Microsoft Research Asia. Since no open-source implementation is available on public channels, it seems that development has been continued internally for the foreseeable future.

Key differences

There are some critical differences between the three analyzed frameworks, which in some cases might force a decision for a specific choice.
For one, only Graph Nets uses TensorFlow as its backend currently. If your solutions rely heavily on the TensorFlow environment. The possibility of using TensorFlow as a backend will be available with v0.5 of DGL. Still, Graph Nets remains to be the only of the listed alternatives that have the potential to become part of the TensorFlow Ecosystem natively.
Furthermore, if you're only looking to reproduce results for an approach from a recent paper or test it on your data, Pytorch Geometric is probably the right choice. It has an astounding amount of implemented algorithms from papers in the field, coupled with ease of integration with standard benchmark datasets, making it stand out for rapid development and validation.
DGL is the only one that has a clear roadmap that is communicated publicly and has a broad base of contributing developers that are an active part of the project.

Which one should I choose?

First, as already mentioned previously, the best possible way to define which one of the libraries is best for you would be to perform the analysis yourself with the tools we've presented.

With this disclaimer out of the way, here are a couple of suggestions for common use-cases:

• Scientific Research: PyTorch Geometric is developed by a Ph.D. student that is working on SOTA algorithms in the field. This library is probably your best bet. From the ease of integration of common benchmark datasets to implementations of other papers, it allows for a seamless integration if you want to quickly test your new findings against the SOTA.
• Production-ready development: Here, it's not as clear cut. With the newest version and full TensorFlow support on its way, the decision between using DGL and Graph Nets is hard to make. With AWS deeply involved, DGL will very likely offer superior support for large-scale applications soon. Otherwise, if you're keen on being able to apply Deepmind's newest research to your applications, then Graph Nets will be the only option.
• Casual hobbyist: If you're interested in testing Graph Neural Networks, no strings attached, the fastest way possible, then there's no beating PyTorch Geometric. The sheer amount of example implementations you can have a look and adjust is astounding. DGL is a close second, necessitating a higher time investment to get going. Moreover, it shows long-term promise with the public roadmap and backing, possibly being a valuable tool in your backback for future applications.

References:
1. Battaglia, Peter W., et al. "Relational inductive biases, deep learning, and graph networks." arXiv preprint arXiv:1806.01261 (2018).
2. Gilmer, Justin, et al. "Neural message passing for quantum chemistry." Proceedings of the 34th International Conference on
Machine Learning-Volume 70. JMLR. org, 2017.
3. Bronstein, Michael M., et al. "Geometric deep learning: going beyond euclidean data." IEEE Signal Processing Magazine 34.4 (2017): 18-42.
4. Fey, Matthias, and Jan Eric Lenssen. "Fast graph representation learning with PyTorch Geometric." arXiv preprint arXiv:1903.02428 (2019).
5. Wang, Minjie, et al. "Deep graph library: Towards efficient and scalable deep learning on graphs." arXiv preprint arXiv:1909.01315 (2019).
6. Fey, Matthias, et al. "SplineCNN: Fast geometric deep learning with continuous B-spline kernels." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.
7. Hanocka, Rana, et al. "MeshCNN: a network with an edge." ACM Transactions on Graphics (TOG) 38.4 (2019): 1-12.