Recent advances in computer vision have come mainly through novel deep learning approaches, hierarchical machine learning models that rely on large amounts of data to be trained on specific tasks. The resulting magnitude and pace of performance improvements have sparked a gold rush for similar applications in other scientific fields.
Among many other fields of study, these developments have spawned the field of Geometric Deep Learning (GDL). We'll explain what the "Geometric" in GDL stands for while also interpreting it in the context of relational inductive bias, a statistical reasoning term coined by DeepMind's researchers in the field.
Some topics in Computer Science are exciting but have only a narrow scope of useful tasks that can be performed with them. GDL is not one of them; we'll delve into some of the many tasks it excels at.
The sections are as follows:
- Introduction
- Geometric Deep Learning
- Statistical Reasoning
- Interesting use-cases
- Graph Segmentation
- Graph Classification
- Real use-cases
- Conclusion
Bring this project to life
Introduction
In the past decade significant advances were made in the areas of machine and deep learning, thanks in large part to a fast-growing amount of computing power and available data combined with new applications of algorithms developed in the '80s and '90s (e.g. backpropagation and LSTMs). One of the biggest beneficiaries of this development was the area of Representation Learning, which is placed among the sub-fields of supervised learning. Representation Learning, often referred to as Feature Learning, is a sub-field of Machine Learning (ML) concerned with algorithms that find the best data representation for a task without manual intervention. It is a direct replacement for Feature Engineering in many applications, which is the field concerned with developing features and descriptors to best perform on other ML tasks.
A prominent example of this is the usage of deep convolutional neural networks (CNNs) for tasks like image classification and object detection, achieving much higher performance on benchmarks than conventional algorithms. Before the rise of deep CNNs the process usually consisted of two stages. One would start by extracting hand-crafted features from the image, and then perform a particular task based on those features. Most successful conventional algorithms relied on variations of this pattern, performing one of these steps or both. With deep CNNs there came a shift towards End-to-End (E2E) learning, which means that learning the underlying representation of the analyzed data is done in an entirely data-driven way, i.e., without specialist input or manipulation.
The first time this approach was (successfully) shown in a broader context was by Krizhevsky et al. In the 2012 ImageNet competition they outperformed the state-of-the-art (SOTA) based on Feature Engineering substantially [6]. This is evident in the chart below, seen in the jump in performance between "SIFT + FVs" and "AlexNet". Furthermore, all of the approaches after that built upon this innovation to further improve performance on this benchmark.
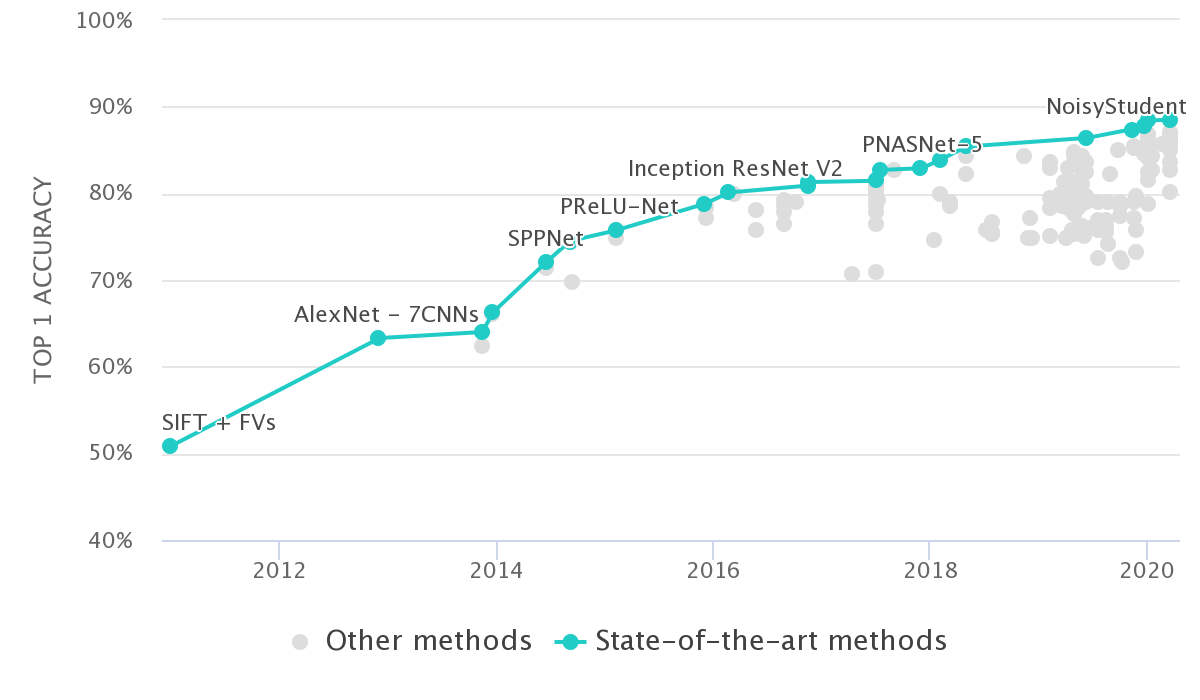
The "deep" in deep learning refers to the number of consecutive layers employed within the neural networks. Regarding the effectiveness of E2E learning, it is interesting to see what the layers learn at each stage. For CNNs applied to images, data representations learned by the networks in an E2E way rely on similar aspects as when done by specialists: by reacting to higher-level features (edges, corners) in shallower layers, and ever more specific compositional features (structures) in the deeper layers. This first breakthrough using deep learning (DL) also sparked other sub-fields of ML to try to take advantage of these new learnings regarding representation learning. Deep Reinforcement Learning using neural networks for value function approximation is one example of many.
In the next section we'll take a look at one recently blossoming field of study with a similar origin, and the main subject of this article.
Geometric Deep Learning
Bronstein et al. first introduced the term Geometric Deep Learning (GDL) in their 2017 article "Geometric deep learning: going beyond euclidean data" [5].
The title is telling; GDL defines the emerging field of research that employs deep learning on non-euclidean data. What exactly is non-euclidean data? An explanation by exclusion is that with non-euclidean data, the shortest valid path between two points is not the Euclidean distance between them. We will use a mesh, or a graph specialization which is very widespread in the field of computer graphics, to visualize this. On the image below, one can see the difference between representing the classic Stanford bunny as a mesh (non-euclidean) or as a grid-like volume (euclidean), in this case, through discretized voxels. The euclidean distance between points A and B is the length of the shortest straight path between them, visualized as the blue line on the image. An exemplary geodesic distance between both points would be more similar to the length of the green line. A geodesic distance is a generalization of the concept of the shortest path for higher dimensions, while the geodesic distance's definition for graphs is usually the shortest path between nodes.
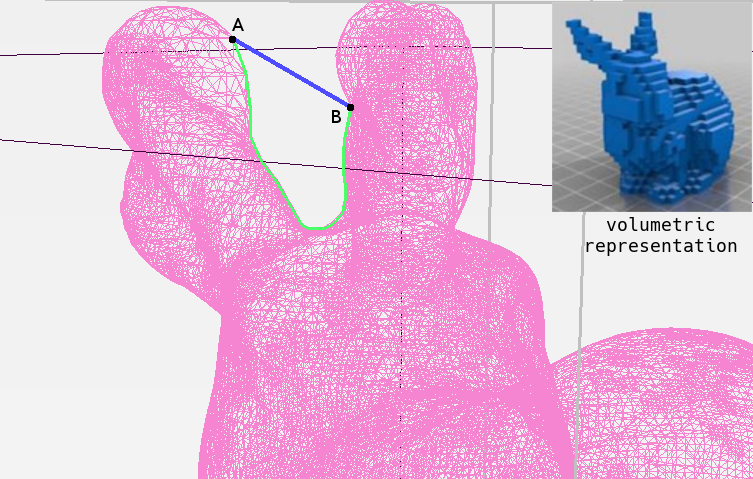
The advantage of interpreting the mesh in a non-euclidean way is that the geodesic distance is more meaningful for tasks performed on it. Think of it this way: in deep CNNs we rely on neighboring pixels likely correlating to one another. To reproduce a similar setting on graphs, we need to take into account a reformulation of the "closeness".
Of course, we can cast inherently non-euclidean data into euclidean data, but this includes a high cost in lost efficiency and performance. This cost is evident in progress on Stanford's ShapeNet dataset for part classification and segmentation. The first neural network to achieve good results on the benchmark presented by Chang et al. relied on a volumetric representation of meshes and Deep Belief Networks for processing them. [4]
A big issue with this approach is how to trade off runtime efficiency with discretization, since the scaling of the problem is cubic. Furthermore, using convolutions on 3D voxels poses the issue of a significant overhead in computations performed on empty 3D space. Since many different objects are represented in the same voxel space, there's no easy way to prevent these empty computations from happening.
Current SOTA approaches perform the tasks mentioned above directly on the meshed structures or transform them into point clouds, achieving far superior performance and runtime. [3][9]
Don't fret, you don't need Graph Theory knowledge for the remainder of this post, yet you should read up to be able to use the software libraries we'll soon have a look at. For an excellent introduction to graphs and the underlying theory you'll need to understand basic concepts in GDL, you can refer to "A Gentle Introduction To Graph Theory" by Vaidehi Joshi. For an in-depth look at further theory needed to understand the algorithms developed in this field, please refer to the survey paper "A comprehensive survey on graph neural networks" by Wu et al. Moreover, the taxonomy introduced in their survey paper can help highlight the parallels to other fields in Deep Learning.
The best-case scenario, of course, would be for you to already recognize possible use-cases based on the data you have at your disposal, or the other way around; the data needed to solve your current problems based on GDL.
We mentioned that GDL pertains to non-euclidean data and also suggested some examples and definitions. Important to note is that in this article we won't cover point clouds, which have advantages of their own but differ significantly from graphs and meshes in what assumptions we can make.
Statistical Reasoning
Overall we want to differentiate between Deductive and Inductive Reasoning. With deductive reasoning, we try to use general terms to make specific claims or come to particular conclusions. An example of this would be the combination of both assertions "All men must die" and "John Doe is a man" to come to the following conclusion: "John Doe must die" (eventually). Inductive reasoning goes the other way around, trying to infer general ideas or conclusions from specific terms. We'll visualize this reasoning with a contemporary example from a German study on the extent of adolescent alienation from nature. A quick test for the reader: What type of cow only yields UHT (long-life) milk?

If your answer was "none", then you are in line with 21% of the interviewed adolescents. A quick roundup of the results can be seen below:
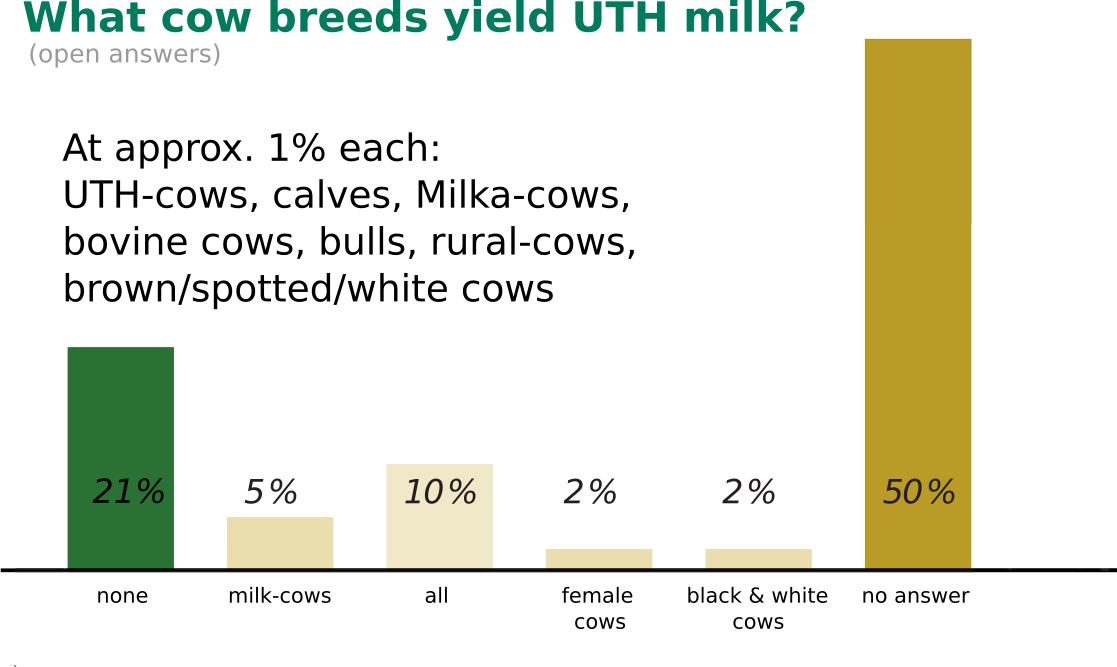
There's a breadth of results to analyze here, but we'll keep to the 1% that thought Milka-cows yield UHT milk. We'll explain this conclusion in terms of inductive reasoning from the children's point of view in the following way: "UHT milk is a special type of milk" and "Milka-cows are a special breed of cow", leading to "Milka-cows yield UHT milk." The issue is that there is no such thing as a Milka-cow. Milka is a chocolate brand from Germany. Their CI's primary color is purple, and their brand mascot accordingly is a purple cow with white spots. It would suffice for these children to read a comic book with "real" cows or visit a farm to change their views for the better. Based on the information they have at their disposal, they come to a wrong conclusion. [2]
As can already be seen from the German Urban Children example, the result of inductive reasoning can be changed either by what patterns the learner is exposed to or by changing the learner's interpretation of the task. Learning that UHT milk is an industrial product also would've helped through deductive reasoning. Disregarding the fact that this information should be common knowledge, had this question not been posed as an open answer, results likely would've been different. The way the question is asked can be seen as an inductive bias in this instance.
To sum this up, we'll borrow from Tom Mitchell's book "Machine Learning":
Thus, we define the inductive bias of a learner as the set of additional assumptions sufficient to justify its inductive inferences as deductive inferences.
Basically, by carefully designing the inductive bias of our algorithms, we can achieve results through inductive inferences that are equal to deductive inferences.
This is desirable since deductive inferences are the best we can make, being provably correct.
Battaglia et. al expand this definition to relational inductive bias, which are inductive biases "which impose constraints on relationships and interactions
among entities in a learning process." [1] In their work they contextualize current neural network components with respect to this definition, and sum this up in the following way:
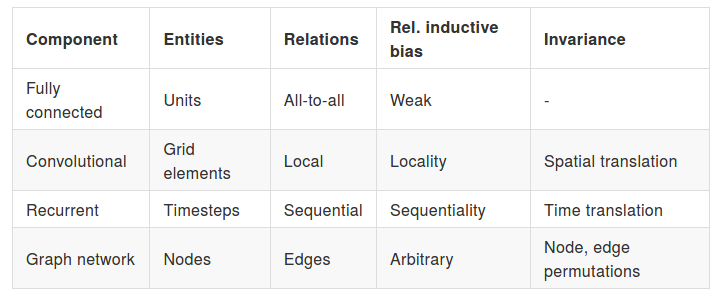
The table above already directly mentions two essential attributes of deep CNNs: local statistics, and invariance to spatial translations. Additionally, by stacking convolutional layers in deep CNNs, we are inducing the network to learn features on different levels of abstraction. This hierarchical composition is also the third main attribute of deep CNNs. What this means is that by sequentially composing layers, we achieve a hierarchy of features that leads to a quantitatively better representation for the supervised task. Altogether, these three aspects are what lend deep CNNs to generalize so well for the image domain. Basically, with deep CNNs, we seem to have hit a sweet spot with respect to the assumptions we choose to constrain and the parameters we need to fit with learning algorithms, leading to good generalization.
Fitting parametric models via gradient descent, unsurprisingly, works best when what you are fitting is already a template of the solution.
— François Chollet (@fchollet) June 1, 2019
Of course, convnets are an instance of this (but in a good way, since their assumptions generalize to all visual data).
Current research in GDL is trying to reach a similar sweet spot, but building upon far more powerful components for reasoning. As mentioned by Francois Chollet in the tweet above, deep CNNs generalize well to all visual data because of the reasons we've already discussed. With GDL on graphs, we're relying on arbitrary relational inductive biases to develop algorithms that can generalize to arbitrary relational data.
Interesting Use-Cases
From the greater Computer Science math corpus, Graph Theory is notorious for being considered the hardest subject in discrete math. Nevertheless, as we will see in this section, it does pay off by allowing us to gain some incredible insight and perform exciting tasks together with deep learning.
Graph Segmentation
Segmentation for graphs is the task of classifying each component of a graph, nodes, or edges. Ground truth labels for such a task are visualized below for the four-legged dataset from the greater COSEG semantic segmentation dataset. In this case, every face has a label belonging to one of the five possible classes: ears, head, torso, legs, and tail. From the face-level information it is trivial to generate node or edge labels, with some heuristics for class overlaps. Currently, both approaches for working directly on meshes as on sampled point clouds achieve SOTA performance on this benchmark. [3][9]
Why is semantic segmentation on this granular level relevant? Well, think of tasks like autonomous cars, which need to continually monitor their environment and interpret what human pedestrians are up to next. Usually pedestrians are represented either as large 3D bounding boxes or as skeletons with more degrees of motion. With better and faster 3D semantic segmentation, many more algorithms for the autonomous car's perception would be feasible, as it would unify both previously mentioned approaches.

Graph Classification
The algorithms in this sub-category receive a graph or sub-graph as their input and predict one of n specified classes with a certainty value coupled to this prediction. This prediction is usually made in a very similar way to Image Classification, in that there are two main parts to the employed networks. The first one is the Feature Extractor, whose job it is to generate an optimal representation for the task at hand from the input data. Then come one or more fully connected layers to constrain the resulting regression to a certain dimensionality, while for multi-class classification, a softmax layer is necessary. Multi-class classification means that for every input we have, more than one class correspondence is possible.
One of many exciting use-cases for this broader task is the classification of 3D facial expressions. Consumer-grade products already come with sensors and compute power enough to generate the needed 3D data structures, and with current approaches we're coming ever closer to also having the algorithms that can reliably interpret them. Gong et al. recently introduced a mesh-based approach that relies only on XYZ-coordinates, without any supplementary feature engineering, which achieves SOTA performance on the 4DFAB with an accuracy of almost 80%. [7][8]
Are There Any "Real" Use-Cases?
Fortunately, the answer to that question is a resounding YES.
I'll keep to one example from an industrial application, and leave some further literature as food for thought.
In both our example use-cases for Graph Segmentation and Graph Classification, the focus was on tasks that come from classical computer vision. GDL also shines in applications where the use of graphs is more common, like knowledge graphs.
From ontotext's knowledge hub:
A knowledge graph (KG) represents a collection of interlinked descriptions of entities – real-world objects, events, situations or
abstract concepts – where:
- Descriptions have a formal structure that allows both people and computers to process them in an efficient and unambiguous manner;
- Entity descriptions contribute to one another, forming a network where each entity represents part of the description of the entities related to it.
A very compelling use-case in times of the coronavirus (COVID-19) is KGCN by the Grakn Labs team. Their example implementation of diagnosis prediction based on KGCN is also worth a read. They make use of data input by doctors and nurses regarding past patients to gather ground truth graph data. Using this ground truth data, they can then learn to predict relations for new patients.
Following our coronavirus example, the network could be taught to predict the probability of this viral infection based on previous cases in the database. The likelihood of a disease, a predicted relation in our knowledge graph, could then be predicted by the network based on the symptoms. This prediction mechanism could be used in hospitals or as a public service as a simple web application. The application could rely on accurate clinical data and inform the user of the likelihood of his viral infection after he inputs his self-diagnosed symptoms. The self-diagnosis could even be taken into account by giving different weights to relations that are input by a user, as opposed to a medic or nurse. In hospitals, these predictions could then serve doctors to either speed up processes or serve as a second opinion to their diagnosis.
Here's some further reading for cross-domain applications:
Graph Neural Solver for Power Systems
https://ieeexplore.ieee.org/abstract/document/8851855

Conclusion
In this post we briefly introduced the topic of Geometric Deep Learning and put it in the context of Deep Learning as a whole. While GDL deals with irregular data structures overall, we focused on graphs and illustrated why they are promising in terms of the learning biases we can introduce.
Finally, we show use-case examples including recent applications, and provide relevant references for those interested in delving deeper.
If this is your first time reading about GDL and it piqued your interest, keep an eye out for upcoming posts on the available libraries and how to use them in practice.
References
1. Battaglia, Peter W., et al. "Relational inductive biases, deep learning, and graph networks." arXiv preprint arXiv:1806.01261 (2018).
2. Brämer, Rainer, ed. Natur: Vergessen?: Erste Befunde des Jugendreports Natur 2010. Information. Medien. Agrar eV, 2010.
3. Hanocka, Rana, et al. "MeshCNN: a network with an edge." ACM Transactions on Graphics (TOG) 38.4 (2019): 1-12.
4. Chang, Angel X., et al. "Shapenet: An information-rich 3d model repository." arXiv preprint arXiv:1512.03012 (2015).
5. Bronstein, Michael M., et al. "Geometric deep learning: going beyond euclidean data." IEEE Signal Processing Magazine 34.4 (2017): 18-42.
6. Krizhevsky, Alex, Ilya Sutskever, and Geoffrey E. Hinton. "Imagenet classification with deep convolutional neural networks." Advances in neural information processing systems. 2012.
7. Gong, Shunwang, et al. "SpiralNet++: A Fast and Highly Efficient Mesh Convolution Operator." Proceedings of the IEEE International Conference on Computer Vision Workshops. 2019.
8. S. Cheng, I. Kotsia, M. Pantic, and S. Zafeiriou. 4dfab: A large scale 4d database for facial expression analysis and biometric applications. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 5117–5126, 2018.
9. Qi, Charles Ruizhongtai, et al. "Pointnet++: Deep hierarchical feature learning on point sets in a metric space." Advances in neural information processing systems. 2017.
10. Mitchell, Tom M. "Machine learning." (1997).













