Generative models are machine learning algorithms that can create new data similar to existing data. Image editing is a growing use of generative models; it entails creating new images or modifying existing ones. We’ll start by defining a few important terms:
GAN Inversion → Given an input image $x$, we infer a latent code w, which is used to reconstruct $x$ as accurately as possible when forwarded through the generator $G$.
Latent Space Manipulation → For a given latent code $w$, we infer a new latent code, $w’$, such that the synthesized image $G(w’)$ portrays a semantically meaningful edit of $G(w)$
To modify an image using a pre-trained image generation model, we would need to first invert the input image into the latent space. To successfully invert an image one needs to find a latent code that reconstructs the input image accurately and allows for its meaningful manipulation. There are 2 aspects of high-quality inversion methods:
The generator should properly reconstruct the given image with the style code obtained from the inversion. In order to determine if there was a proper reconstruction of an image we focus on 2 properties:
- Distortion: this is the per-image input-output similarity
- Perceptual quality: this is a measure of the photorealism of an image
- Editability: it should be possible to best leverage the editing capabilities of the latent space to obtain meaningful and realistic edits of the given image
Inversion methods operate in the different ways highlighted below:
- Learning an encoder that maps a given image to latent space (e.g. an autoencoder) → This method is fast, but it struggles to generalize beyond the training method
- Select an initial random latent code, and optimize it using gradient descent to minimize the error for the given image
- Using a hybrid approach combining both aforementioned methods
Optimizing the latent vector achieves low distortion, but it takes a longer time to invert the image and the images are less editable (tradeoff with editability).
In order to find a meaningful direction in the high-dimensional latent space, recent works have proposed:
- Having one latent vector handling the identity, and another vector handling the pose, expression, and illumination of the image.
- Taking a low-resolution image and searching the latent space for a high-resolution version of the image using direct optimization.
- Performing image-to-image translation by directly encoding input images into the latent codes representing the desired transformation.
In this blog post, I’ll review some of the landmark GAN inversion methods that influenced the current generative models today. A lot of these methods reference StyleGAN; this is because it has had a monumental influence in the image generation domain. Recall that StyleGAN consists of a mapping function that maps a latent code z into a style code w and a generator that takes in the style code, replicates it several times depending on the desired resolution, and then generates an image.
1. Encoder for Editing (E4E)
The e4e encoder is specifically designed to output latent codes that ensure further editing beyond the style space, $S$. In this project, they describe the distribution of the W latent space as the range of the mapping function. Because it is impossible to invert every real image into StyleGAN’s latent space, the expressiveness of the generator can be increased by inputting k different style codes instead of a single vector. k is the number of style inputs of the generator. This new space is known as $W^k$. Even more expressive power can be achieved by inputting style codes that are outside the range of StyleGAN’s mapping function. This extension can be applied by taking a single style code and replacing it, or taking k different style codes. These extensions are denoted by $W_$ and $W^k$ respectively. (The popular $W+$ space is simply $W^{k=18}$).
Distortion-Editability & Distortion-Perception Tradeoff
$W_^k$ achieves lower distortion than W which is more editable. W is more ‘well-behaved’ and has better perceptual quality compared to $W_^k$. However, the combined effects of the higher dimensionality of $W_*^k$ and the robustness of the StyleGAN architecture have far greater expressive power. These tradeoffs are controlled by the proximity to W. In this project, they differentiate between different regions of the latent space.
How Did They Design Their Encoder?
They design an encoder that infers latent codes in the space of $W_^k$. They design two principles that ensure that the encoder maps into regions in $W_^k$ that lie close to $W$. These include:
- Limiting the Variance Between the Different Style Codes (encouraging them to be identical)
To achieve this they use a progressive training scheme. Common encoders are trained to learn each latent code $w_i$ separately and simultaneously by mapping from the image directly into the latent space $W_^k$. Conversely, this encoder infers a single latent code $w$, and a set of offsets from $w$ for the different inputs. At the start of training the encoder is trained to infer a single $W_$ code. The network then gradually grows to learn different $\triangle_i$ for each $i$ sequentially. In order to explicitly force proximity to $W_*$, we add an $L_2$ delta-regularization loss - Minimizing Deviation From $W^k$
To encourage the individual style codes to lie within the actual distribution of $W$, they adopt a latent discriminator (trained adversarially) to discriminate real samples from the W space (from StyleGAN’s mapping function) and the encoder’s learned latent codes.
This latent discriminator addresses the challenge of learning to infer latent codes that belong to a distribution that cannot be explicitly modeled. The discriminator encourages the encoder to infer latent codes that lie within $W$ as opposed to $W_*$.
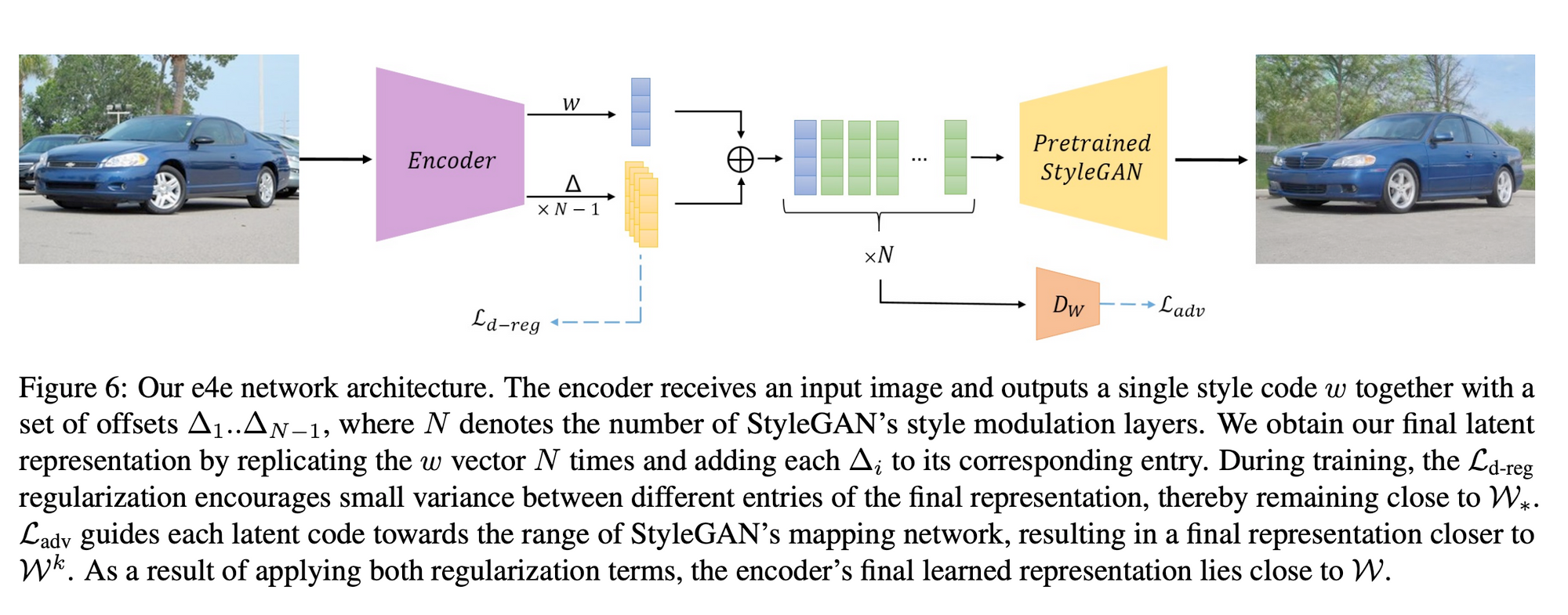
Although this encoder is inspired by the Pixel2Pixel (pSp) encoder which outputs N style codes in parallel, it only outputs a single base style code and a series of $N-1$ offset vectors. The offsets are summed up with the base style code to get the final N style codes which are then fed into a pretrained StyleGAN2 generator to obtain the reconstructed image.
Losses
They train the encoder with losses that ensure low distortion, and losses that explicitly encourage the generated style codes to remain close to $W$, thereby increasing the perceptual quality and editability of the generated images.
- Distortion:
In order to maintain low distortion, they focus on identity loss - which is specifically designed to assist in the accurate inversion of real images in the facial domain. Inspired by the identity loss, they created a novel loss function, $\textbf{L\_{sim}}$ to find the cosine similarity between the feature embeddings of the reconstructed image and its source image. They use a ResNet-50 network trained on MOCOv2 to extract the feature vectors of the source and reconstructed image.
In addition to the $L_{sim}$ loss they also implement the $\textbf{L\_2}$ loss and the LPIPS loss function to measure structural similarities between both images. The summation of these 3 results in the finalized distortion loss. - Perceptual Quality and Editability:
They apply a delta-regularization loss to ensure proximity to $W_*$ when learning the offsets $\triangle_i$. They also use an adversarial loss using our latent discriminator, which encourages each learned style code to lie within the distribution $W$.
2. Image2StyleGAN
In this project, the authors explored the sensitivity of StyleGAN embeddings to affine transformations (translation, resizing, and rotation), and concluded that these transformations have a degrading effect on the generated images e.g blurring and degradation of finer details.
When evaluating the different latent spaces Z and W, the authors noted that it was challenging to embed images into W or Z directly. They proposed to embed into an extended latent space, coined W + . W + is a concatenation of 18 different 512-dimensional w vectors, one for each layer of the StyleGAN architecture, that can each receive input via AdaIn. This enabled a number of useful capabilities from the previously more rigid, albeit powerful, architecture.
Image Morphing → Given two embedded images with their respective la- tent vectors w1 and w2, morphing is computed by linear interpolation, $w = λw1 + (1 − λ)w2, λ ∈ (0, 1)$, and subsequent image generation using the new code w to effectively add perceptual changes to the output.
Style Transfer → Given two latent codes w1 and w2, style transfer is computed by a crossover operation. They apply one latent code for the first 9 layers and another code for the last 9 layers. StyleGAN is able to transfer the low-level features i.e. color and texture, but fails on tasks transferring the contextual structure of the image.
Expression Transformation → Given three input vectors $w1,w2,w3$, expression transfer is computed as $w=w1+λ(w3−w2)$:
- $w1$: latent code of the target image
- $w2$: corresponds to a neutral expression of the source image
- $w3$: corresponds to a more distinct expression
To eliminate the noise (e.g. background noise), they heuristically set a lower bound threshold on the $L_2$− norm of the channels of difference latent code, below which, the channel is replaced by a zero vector.
How Do We Embed an Image Into W+?
Starting from a suitable initialization $w$, we search for an optimized vector $w∗$ that minimizes the loss function that measures the similarity between the given image and the image generated from $w∗$.
3. StyleCLIP
This project aims to provide a more intuitive method for image editing in the latent space. The authors note that prior image manipulation techniques relied on manually examining the results, an extensively annotated dataset, and pre-trained classifiers (like in Style Space). Another note is that it is only possible to have image manipulations along a preset semantic direction which is limiting to a user’s creativity.
They proposed a few techniques to help achieve this goal:
- Text-guided latent optimization where the CLIP model is used as a loss network
- A latent residual mapper, trained for a specific text prompt → When given a starting point in the latent space, the mapper yields a local step in latent space
- A method for mapping a text prompt into an input-agnostic direction in StyleGAN’s style space, providing control over the manipulation strength as well as the degree of disentanglement
Method 1: Latent Optimization
Given a source code $w \in W+$, and a directive in natural language, or a text prompt t, they generated an image from $G(w)$, and then found the cosine distance between the CLIP embeddings of the two arguments presented to the discriminator $D(G(w),t)$.
The similarity of the generated image to the input image is controlled by the $L_2$ distance in the latent space and by the identity loss. $R$ is a pre-trained ArcFace network for face recognition, and the operation $\langle R(G(w_S)), R(G(w)) \rangle$ computes the cosine similarity between its arguments.
They showed they could optimize this problem using gradient descent by back-propagating the gradient of the adversarial objective function, through the fixed StyleGAN generator and the CLIP image encoder.
For this method, the input images are inverted into the $W+$ space using the e4e encoder. Visual changes that highly edit the image have a lower identity score, but may have a stable or high CLIP cosine score.
This editing method is versatile because it optimizes for each text-image pair, but it takes several minutes to optimize for a single sample. Additionally, it is very sensitive to the values in its parameters.
Method 2: Latent Residual Mapper
In this method, a mapping network is trained for a specific text prompt t, to infer a manipulation step $M_t(w)$ in the $W+$ space for any given latent image embedding.
Based on the design of the StyleGAN generator, whose layers contain different levels of details (coarse, medium, fine), the authors design their mapper network accordingly with three fully connected networks for each level of detail. The networks can be used in unison or only a subset can be used.
The loss function ensures that the attributes are manipulated according to the text prompt while maintaining the other visual attributes of the image. They use the CLIP loss to measure the faithfulness to the text prompt, and they use the $L_2$ distance to measure the identity loss except when the edit is meant to change the identity loss.
The mapper determines a custom manipulation step for each input image, and therefore determines the extent to which the direction of the step varies over different inputs.
To test this mapper:
- They inverted the CelebA test set using the e4e encoder to obtain the latent vectors and passed these vectors into several trained mappers.
- They computed the cosine similarity between all pairs of the resulting manipulation directions (The pairs mentioned here are the input text prompt and the edited image)
- The cosine similarity score has a significantly high meaning. Enough that, although the mapper infers manipulation steps that are adapted to the input image, the directions given for the training image are not that different from the directions given for the test image. Regardless of the starting point (input image), the direction of the manipulation step for each text prompt is largely the same for all inputs.
- There isn’t a lot of variation in this method although the inference time tends to be fast (this is a slight disadvantage). Because of the lack of variation in manipulation directions, the mapper also doesn’t do too well with fine-frained disentangled manipulation.
Method 3: Global Mapper
They propose a method for mapping a single text prompt into a single, global direction in StyleGAN’s Style Space $S$ which is the most disentangled latent space. Given a text prompt indicating a desired attribute, they sought a manipulation direction $∆s$, such that $G(s + α∆s)$ yielded an image where that attribute is introduced or amplified, without significantly affecting other attributes. As a result, the condition and identity loss are low. They used the term $\alpha$ to denote the manipulation strength
How to Create a Global Mapper?
- They used CLIP’s language encoder to encode the text edit instruction, and map this into a manipulation direction $∆s$ in $S$. To get a stable $∆t$ from natural language requires some level of prompt engineering.
- In order to get $∆s$ from $∆t$, they can assess the relevance of each style channel to the target attribute.
An important note that the authors make is that it is possible for the text embedding and the image embeddings to exist in different manifolds. An image may contain more visual attributes than can be encoded by a single text prompt, and vice versa.
Even though there isn’t a specific mapping between the text and image manifolds the directions of change within the CLIP space for a text-image pair are roughly collinear (Large cosine similarity) after normalizing their vectors.
- Given a pair of images $G(s) \text{ and } G(s+α∆s)$, they denote their image embeddings $I$ as $i \text{ and } i + ∆i$ respectively, the difference between the two images in the CLIP space is $\triangle i$.
- Given a text instruction $\triangle t$ and assuming collinearity between $\triangle t$ and $\triangle i$, we can determine a manipulation direction $\triangle s$ by assessing the relevance of each channel in $S$ to the direction $\triangle i$.
How to Yield a Style Space $S$ Manipulation Direction $\triangle s$?
- The goal is to construct a style space manipulation direction $\triangle s$ that would yield a change $\triangle i$ that is collinear with the target direction $\triangle t$
- They assessed the relevance of each channel $c$ of $S$ to a given direction $\triangle i$ in CLIP’s joining embedding space
- They denoted the CLIP space direction between the images $\triangle i$ as $\triangle i_c$. Therefore, the relevance of channel c to the target manipulation, $R_c(\triangle i)$ was shown as the mean projection of $\triangle i_c \text{ onto } \triangle i$
- Once they estimated the relevance of each channel $R_c$, they could ignore the channels whose $R_c$ falls below a certain threshold $\beta$
- The $\beta$ variable is used to control the degree of disentangled manipulation → Using higher threshold values results in more disentangled manipulations, but at the same time, the visual effect of the manipulation is reduced.
Example of this from the paper 🔽

Summary
There are many more methods that have been proposed for GAN image inversion, however, I hope that the few highlighted in this article get you in the rhythm of understanding some fundamentals of image inversion. A great next step would be understanding how image styling information is embedded into the diffusion process in the state-of-the-art diffusion models and contrasting that with GAN inversion.
CITATIONS:
- Tov, Omer, et al. "Designing an encoder for stylegan image manipulation." ACM Transactions on Graphics (TOG) 40.4 (2021): 1-14.
- Abdal, Rameen, Yipeng Qin, and Peter Wonka. "Image2stylegan: How to embed images into the stylegan latent space?." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019.
- Karras, Tero, et al. "Analyzing and improving the image quality of stylegan." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020.
- Patashnik, Or, et al. "Styleclip: Text-driven manipulation of stylegan imagery." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021.











