Recently, deep learning (DL) based natural language processing (NLP) has become one of the mainstays of study because to the substantial performance gains it can provide to a variety of NLP tasks. Machine learning models, however, need large amounts of data to function properly. The negative is that it is expensive to acquire data within a certain genre for model training, limiting the applicability of such models to other domains, languages, areas, or styles. Meta-learning methods are starting to get more attention as a means of addressing these issues.
Meta-learning, or Learning to Learn, aims to learn better learning algorithms, including better parameter initialization (Finn et al., 2017), optimization strategy (Andrychowicz et al., 2016; Ravi and Larochelle, 2017), network architecture (Zoph and Le, 2017; Zoph et al., 2018; Pham et al., 2018a), distance metrics (Vinyals et al., 2016; Gao et al., 2019a; Sung et al., 2018), and beyond (Mishra et al., 2018). Meta-learning allows
faster fine-tuning, converges to better performance, yields more generalizable models, and it achieves outstanding results for few-shot image classificaition (Triantafillou et al., 2020).
Optimization and Loss Function in Machine Learning for Inference with Parametrized Functions
Finding a function fθ(x) for inference from training data that is parametrized by model parameters is the main objective of machine learning (ML). Machine translation (MT) takes as input a sentence x and outputs a translated version of that sentence fθ(x), whereas automated speech recognition (ASR) takes as input an utterance x and outputs a transcribed version of that utterance, fθ(x). In DL, θ are the network parameters, or weights and biases of a network. To
learn θ, there is a loss function l(θ; D), where D is a set of paired examples for training parameters.
D = {(x1, y1), (x2, y2), ..., (xK , yK )}
where xk is the input to the function, yk is the actual value, and K is the total number of instances in dataset D. We define the loss function l(θ; D), as follows:
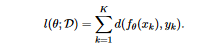
where the "distance" between the function output fθ(xk) and the ground truth yk is denoted by the expression d(fθ(xk), yk). When solving a classification problem, d(.,.) could be the cross-entropy, while when solving a regression problem, it might be the L1/L2 distance. We perform the following optimization problem to find the best parameter set θ∗ for inference by minimizing the loss function l(θ; D).
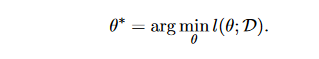
In meta-learning, the aim is to learn a learning algorithm. This kind of process can be interpreted as a function denoted as Fφ(.).
The input of the function Fφ(.) is the training data which is prepared in order to learn the model parameters. The output of the function Fφ(.) is the learned model parameters, i.e., θ∗ in above equation. Learning algorithm Fφ(.) is parameterized by meta-parameters φ which are the parameters that we want to learn in meta-learning.
The meta-parameters φ can include initial parameters, learning rate, network architecture, etc., depending on the specific learning algorithm being used.
Some approaches in Meta-Learning for Enhanced Learning Algorithms
Different meta-learning approaches focus on learning different components of the learning algorithm. For example, model-agnostic meta-learning (MAML) focuses on learning initial parameters while learning to compare methods like Prototypical Network learn the latent representation of the inputs and their distance metrics for comparison.
Network architecture search (NAS) is another meta-learning approach that attempts to learn the network architecture. Meta-learning tries to enhance the efficiency and generalizability of learning algorithms and has been successful in several natural language processing (NLP) tasks.
Meta-Learning: Enhancing Learning Algorithms through Task-based Parameter Optimization"
To learn meta-parameters φ, meta-training tasks Ttrain are required:
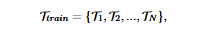
In Meta-learning, a task is represented as Tn where n = the task number and N = total of tasks in the training set (Ttrain). As a general rule, all the tasks in Ttrain belong to the same problem of NLP like question answering (QA) but from different corpora. Nonetheless, it is also possible to have tasks from various problems.
Each task Tn has a support set Sn and a query set Qn. Both Sn and Qn turn out to be similar to the dataset D referred earlier in this article. The support set Sn plays the role of the training data in typical machine learning (ML) and the query set Qn, is equivalent to the testing data.
However, in the context of meta-learning, the terms support and query sets are substituted for training and testing sets to avoid a kind of confusion.
The support set is used to learn a model that can generalize in learning of new tasks and the query set is used for evaluation of the performance of the model on the new task.
The loss function is written as L(φ; Ttrain), where φ stands for the parameters of the learning algorithm and Ttrain is the training tasks.
The below formula measures how “bad” a certain learning algorithm is on some specified training tasks. The performance of the learning algorithm is evaluated over every single task in the training set Ttrain. Meta-learning aims at improving the performance of the learning algorithm on new tasks and hence, optimizes loss function on training tasks.
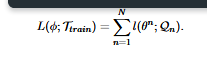
To get l(θn; Qn), the process includes the usage of a support set Sn for every task Tn in Ttrain. The learning algorithm Fφ is used to learn a model from the support set Sn, which has denoted as θn.
The learned model θn approaches near to be an exact equivalent of a typical machine learning training process. This step of using the support set Sn to learn a model is called within-task training. Having learnt the model θn, it is then tested on Qn in order to get l(θn; Qn).
This step of testing the learned model on Qn is referred to as within-task testing.
The entire process of within-task training followed by within-task testing is called an episode.
Task-training
A key part of meta-learning is task training. This entails the training of a model concerning a set of related tasks so that it can enhance its ability to learn new tasks. There are number of ways through which task training can be performed like training on a set of tasks with similar structures or training on a set of tasks with varying levels of difficulty. The goal of task-training is the improvement of model ability for generalization on new tasks by exposing it to a set of diverse training examples.
In the context of natural language processing, task-training has been recognized to have a positive impact on improved performance of models into several tasks like text classification, sentiment analysis as well as machine translation.
Optimization-Based Meta-Learning: Learning Meta-Parameters φ for Enhanced Model Performance
The optimization task below is solved to learn meta-parameteres φ:
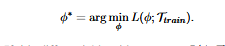
In the above formula, the ϕ is used to represent the model parameters.
The symbol Ttrain represents the dataset for training a machine learning model.
The function L(ϕ;TTrain ) represents the loss function that represents how well the model performs on the training dataset.
The optimization problem seeks optimal values of the parameters ϕ to minimize the loss function L(ϕ;Ttrain ).
ϕ∗ represents optimized values of the parameters which minimize the loss function against the training dataset.
Cross-task training
Cross-task training is a process of finding meta-parameters that parameterize the learning algorithm by running many episodes on meta-training tasks.
It involves training a model on the support set of a domain and evaluating it on the query set in the same domain, which can be considered as domain adaptation.
With a sufficiently large set of tasks in Ttrain, then the cross-task training finds meta-parameters that work well on a wide range of domains and thus also works well on the tasks in T test containing the domains unseen during cross-task training.
Conclusion
Meta-learning, commonly known as “learning to learn”, is an aspect of Artificial Intelligence (AI), which attempts to develop models that can adapt more rapidly and efficiently to new tasks so that they become better performers over time. Meta-learning algorithms attempt to train models that acquire generalized knowledge from different types of tasks and can transfer this generalized knowledge on new tasks with minimal retraining. In opposition to classical machine learning, inasmuch as models are usually trained for a single task; in meta-learning, such models would be used for many tasks.
References













