Introduction
Algebraic word problems take the form of narratives or scenarios expressed as mathematical equations. Algebraic equations must be used to determine the values of the unknowns in these problems. Algebraic word problems can be solved by following a series of steps, starting with reading and understanding the problem statement, moving on to identifying the variables and their relationships, and culminating in setting up the equations and solving for the unknown.
Accurately translating the words of the problem into mathematical expressions and equations is critical to finding the right answer.
Solving Word Problems in Algebra
To solve an algebra word problem, one must first extract information from the question by understanding its language, and then use mathematical reasoning to arrive at an answer. As a result, it provides a valuable experiment for validating the framework. From the dataset used by Koncel-Kedziorski et al. (2015), the authors select a specific type of addition and subtraction questions to use in their study. To encode the information in the questions, the authors define the predicates has/4, transfer/5, and total/4 as shown below:
has(entity, quantity, time stamp, k/q).
transfer(entity1, entity2, quantity, time stamp, k/q).
total(entity, quantity, time stamp, k/q).The predicate has/4 defines that an entity has a certain quantity of some objects, at a particular time stamp and it either constitutes knowledge facts (denoted k) or a question (denoted q).
The transfer/5 predicate defines that an entity1 has transferred a certain quantity
of objects, to entity2 at a particular time stamp and that this information is part of the knowledge facts k or is the query q.
Finally, the total/4 predicate defines that an entity has a total amount of some objects equal to the quantity, at a particular time stamp and that this information is part of the knowledge facts k or is the query q.
Simple s(CASP) criteria are used to compute the solution. Simple Algebra word problems using the has/4, transfer/5, and total/4 predicate can be solved by following these rules. Here is a sample problem that shows how to construct predicates to describe knowledge.
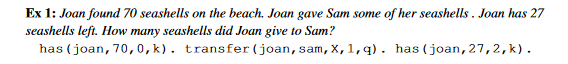
According to the STAR methodology, the authors use an LLM to transform the knowledge contained in the selected algebraic problem to the predicates described above. The predicates thus obtained (including the query) along with the rules then constitute the logic program. The query predicate is then tested against the program to answer the word problem.
Experiments and Results
The word problems used in this dataset are from a collection that was made available by Koncel-Kedziorski et al. (2015). The collection consists of 91 different problems.
We provide a context of a few problems with their corresponding predicates to the GPT-3 models and then use each problem as a prompt along with the context for the model to generate the facts and the query predicate(s) corresponding to the new problem
The authors use the common sense rules combined with the generated predicates (facts) as a logic program and query the program using the query predicate. Then, for each problem, they compare the human-determined solution with the solution generated by the logic program. The GPT-3 model is what they use as a starting point for direct answer prediction.
They conducted their experiments on a smaller set of 12 problems to further analyze the LLM's inaccuracies in generating predicates. Because their method can be explained (unlike the pure response prediction method), they were able to figure out what went wrong and then try to fix it by adding more problems to the context. After many iterations, the final context of the GPT-3 model consists of 24 problems. Table 2 shows the data they collected from their tests.

On the set of 67 problems used for testing, the text-davinci-003-Direct and text-davinci-003-STAR get a perfect score of 100 percent accuracy. According to the results of our tests, algebraic word problems that require simple reasoning can be easily handled by large LLMs. While our STAR method is as accurate as other approaches, it also has the ability to provide justificationsn, making it explainable. Below is a representation of the reasoning tree generated by s(CASP) (Arias et al. (2020)) for the problem presented above, for which the computed solution was 43.
JUSTIFICATION_TREE:
transfer(joan,sam,43,1,q) :-
has(joan,70,0,k),
has(sam,27,2,k),
43 #= 70-27.
global_constraint.Conclusion
One of the most significant shortcomings of LLMs is their poor performance on mathematical. Because the computation in this method is performed outside the reasoning process, it eliminates the possibility of the LLM making computational errors and ensures that the method is trustworthy.
Reference













