Introduction
Natural language reasoning is an application of deductive reasoning that draws a conclusion from given premises and rules stated in natural language. The goal of neural network architecture research is to figure out how to use these premises and rules to draw new conclusions.
In the past, a comparable task would have been performed by systems that were pre-programmed with the knowledge already stored in a formal way, as well as the rules to follow to infer new information. However, the use of formal representations has proven to be a significant obstacle for this branch of research (Mark A. Musen, 1988). Now, thanks to the development of transformers and the exceptional performance they have shown in a wide variety of NLP tasks, it is possible to avoid the need for formal representations and to have transformers participate directly in reasoning through the use of natural language. In this article, we will highlight some of the most important transformers for natural language reasoning tasks.
RoBERTa
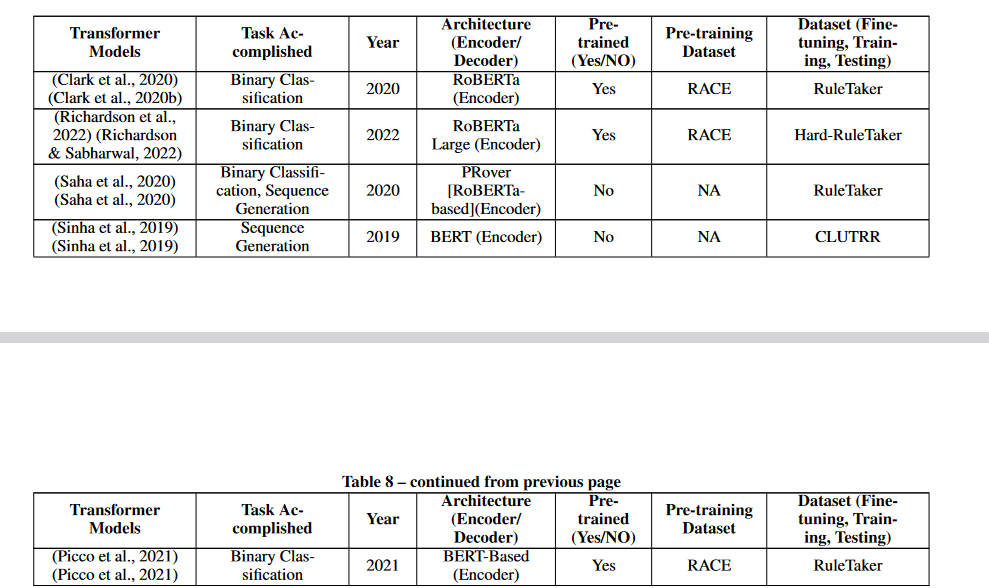
In the research conducted in 2020 by Clark et al. (2020b), the transformer was given a binary classification task to perform. The goal of this work was to determine whether or not a given proposition could be derived from a given collection of premises and rules expressed in natural language.
It was pre-trained on a dataset consisting of questions from standardized high school tests that required the use of reasoning skills. Because of this pre-training, the Transformer was able to achieve a very high level of accuracy on the test dataset, which was 98%. The data set contained hypotheses that were randomly selected and generated using predefined sets of names and characteristics.
The task asked the transformer to determine whether the given premises and rules (the context) led to the conclusion that the given claim (the assertion) followed from them (Clark et al., 2020b).
RoBERTa-Large
In the study by Richardson and Sabharwal (2022), the authors attempted to address a shortcoming identified in the paper by Clark et al. (2020b) regarding the technique used to generate the dataset. They pointed out that the uniform random selection of theories used in (Clark et al., 2020b) did not always result in challenging cases.
They provided an innovative way to generate challenging data sets for algorithmic reasoning to get around this problem. The most important component of their technique is an approach that takes hard examples of standard SAT propositional formulas and translates them into natural language using a predetermined collection of English rule languages. By following this technique, they were able to build a more challenging dataset, which is important for training robust models and for trustworthy evaluation.
The authors conducted experiments in which they evaluated the models trained on the dataset from (Clark et al., 2020b) on their newly built dataset. The goal of these tests was to illustrate the effectiveness of the technique they had developed. According to the results, the models achieved an accuracy of 57.7% and 59.6% for T5 and RoBERTa, respectively. These results highlight the fact that models trained on simple datasets may not be able to solve challenging cases.
PRover
In a separate but similar paper, Saha et al. (2020) developed a model they call PRover. This model is an interpretable joint transformer that has the potential to provide a matching proof that is accurate 87% of the time. The problem that PRover attempts to solve is identical to the one studied by Clark et al. (2020b) and Richardson & Sabharwal (2022), which is to determine whether or not a particular conclusion follows logically from the premises and rules presented.
The proof generated by PRover is given in the form of a directed graph, where the propositions and rules are represented by nodes, and the edges of the graph indicate which new propositions result from the application of the rules to the previous propositions. In general, the strategy proposed by Saha et al. (2020) is a promising way to achieve interpretable and correct reasoning models.
BERT-based
As described in (Picco et al., 2021), improved generalization performance on the RuleTaker dataset was achieved by using a BERT-based architecture (called a "neural unifier"). Even when trained only on shallow queries, the model should be able to answer complex questions, so the authors tried to mimic certain aspects of the backward chaining reasoning technique. This should improve the model's ability to handle questions that require more than one step to answer.
The neural unifier has two components: a fact-checking unit and a unification unit, both of which are typical BERT transformers.
- The fact-checking unit is designed to determine whether an embedding vector C represents a knowledge base from which a query of depth 0 (represented by the embedding vector q-0) follows.
- The unification unit performs backward chaining by taking the embedding vector q-n of a depth-n query and the embedding vector of the knowledge base, vector C, as input and trying to predict an embedding vector q0.
BERT
In contrast to the above work, Sinha et al. (2019) created a dataset called CLUTRR in which the rules are not provided in the input. Instead, the BERT transformer model must extract the links between entities and infer the rules that govern them. For example, if the network is provided with a knowledge base containing assertions such as "Alice is Bob's mother" and "Jim is Alice's father", it can infer that "Jim is Bob's grandfather".
Automated symbolic reasoning
The branch of computer science known as automated symbolic reasoning focuses on using computers to solve logical problems such as SAT solving and theorem proving. Heuristic search techniques have long been the standard method for solving such problems. However, recent research has explored the possibility of improving the effectiveness and efficiency of such approaches by using learning-based methods.
One method is to study how classical algorithms choose among multiple heuristics to find the most effective one. Another is to use a solution based on learning data from start to the end. Results from both methods have been promising, and both hold promise for future developments in automated symbolic reasoning (Kurin et al., 2020; Selsam et al., 2019). Some transformer-based models have performed very well in automated symbolic reasoning tasks.
SATformer
To solve the SAT problem for boolean formulae, Shi et al. introduced SATformer in 2022 (Shi et al., 2021)—a hierarchical transformer design that provides a comprehensive, learning-based solution to the issue. It is common practice to convert a boolean formula into its conjunctive normal form (CNF) before feeding it into a SAT solver. Each sentence in the CNF formula is a disjunction of the literals that make up the formula, hence the formula itself is a conjunction of boolean variables and their negations. Using boolean variables in a CNF formula would result in the notation (A OR B) AND (NOT A OR C), where the clauses (A OR B) and (NOT A OR C) are composed entirely of literals.
The authors employ a graph neural network (GNN) to obtain the embeddings of the clauses in the CNF formula. SATformer then operates on these clause embeddings to capture the interdependencies among clauses, with the self-attention weight being trained to be high when groups of clauses that could potentially lead to an unsatisfiable formula are attended together, and low otherwise. Through this approach, SATformer efficiently learns the correlations between clauses, resulting in improved SAT prediction capabilities (Shi et al., 2022b)
TRSAT
In 2021, Shi et al. performed research on MaxSAT, a special case of the boolean SAT issue, and presented a transformer model called TRSAT, which functions as an end-to-end learning-based SAT solver (Shi et al., 2021). The satisfiability of a linear temporal formula (Pnueli, 1977) is analogous to the boolean SAT in which the objective is to find a satisfactory symbolic trace to the formula given the linear temporal formulation.
Transformer
Hahn et al. (2021) handled challenging problems than the binary classification tasks previously studied by addressing the boolean SAT issue and the temporal satisfiability problem. The objective of these issues is not to merely categorize whether or not a given formula is met, but rather to construct a suitable sequence assignment for that formula. Using classical solvers, the authors created linear temporal formulae with satisfying symbolic traces and boolean formulas with corresponding satisfying partial assignments to create their datasets. To perform this operation, they used a conventional transformer design. Some of the satisfying traces generated by the Transformer were not seen during training, demonstrating its capacity to solve the issue and not only copy the behavior of the traditional solvers.
GPT-f
Polu and Sutskever (2020) introduced GPT-F, an automated prover and proof assistant that, like GPT-2 and GPT-3, is built on a decoder-only transformers architecture. The set.mm dataset, which includes over 38,000 proofs, was used to train GPT-F. The authors' largest model has 774 million trainable parameters over 36 layers. Many of the innovative proofs generated by this deep learning network have been adopted by groups and libraries devoted to the study of mathematics.
Conclusion
In this article we have talked about some powerfull transformers that we can use for natural language reasoning. There has been some encouraging research on the use of transformers for theorem proving and propositional reasoning, but their performance on natural language reasoning tasks is still far from ideal. Further research is needed to improve the reasoning abilities of transformers and to find new, challenging tasks for them. Despite these caveats, transformer-based models have undoubtedly advanced the state of the art in natural language processing and opened up exciting new avenues for research in language understanding and reasoning.
Reference














