During the early days of attention mechanisms in computer vision, one paper published at CVPR 2018 (and TPAMI), Squeeze and Excitation Networks, introduced a novel channel attention mechanism. This simple yet efficient add-on module can be added to any baseline architecture to get an improvement in performance, with negligible computational overhead.
In this article we'll cover Squeeze-and-Excitation Networks in four parts. First, we will understand the intuition behind why channel attention is important by visiting some aspects in modern photography techniques. Then we'll advance to the methodology involved in computing the channel attention in Squeeze-and-Excitation (SE) blocks. Following this, we will dissect the impact of Squeeze-and-Excitation (SE) blocks in standard architectures, while evaluating them on different computer vision tasks. We will end with a critique of the paper regarding certain shortcomings in the method proposed.
Bring this project to life
Table of Contents
- Frame Selection in Modern Photography
- Channel Attention in Convolutional Neural Networks
- Squeeze-and-Excitation Networks
- Code
- MBConv in Efficient Nets
- Benchmarks
- Shortcomings
- References
Frame Selection in Modern Photography

As modern photography has grown through generations of improvements in intelligent mechanisms to capture the best shot, one of the most subtle techniques that has gone under the radar is selection of the best frame shots for a still photo. This is a common feature in certain smart phones.
There are many variables in a still photograph. Two photographs of a subject taken a second apart from each other, under the same conditions and in the same environment, can still differ a lot. For example, their eyes might be closed in one of the two photographs. To get the best shot, it is much better to capture multiple frames at the instant the photograph is taken, so that the photographer has the choice of selecting the best frame from all frames captured. Nowadays this is done in an automated, intelligent fashion. Smart phones like the Google Pixel have the ability to pick the best frame from all the available frames taken when capturing a single photograph. This intelligent mechanism is conditioned by different factors like the lighting, contrast, blur, background distortion, etc. In an abstract way, the intelligent mechanism is selecting the frame which contains the best representative information of the photograph.
In terms of modern convolutional neural network architectures, you can think of the frames as the channels in a tensor computed by a convolutional layer. This tensor is usually denoted by a (B, C, H, W) dimensionality, where B refers to the batch size, C refers to the channels, and the H, W refers to the spatial dimensions of the feature maps (H represents the height and W represents the width). The channels are the result of the convolutional filters deriving different features from the input. However, the channels might not have the same representative importance. As some channels might be more important than others, it makes sense to apply a weight to the channels based on their importance before propagating to the next layer.
We will use this as a foundational understanding of the importance of channel attention, which we will go through in the following sections.
Channel Attention
Based on the intuition described in the previous section, let's go in-depth into why channel attention is a crucial component for improving generalization capabilities of a deep convolutional neural network architecture.
To recap, in a convolutional neural network, there are two major components:
- The input tensor (usually a four-dimensional tensor) represented by the dimensions (B, C, H, W).
- The trainable convolutional filters which contain the weights for that layer.
The convolutional filters are responsible for constructing the feature maps based on the learned weights within those filters. While some filters learn edges, others learn textures, and collectively they learn different feature representations of the target class information within the image embedded by the input tensor. Thus, the number of channels represents the number of convolutional filters which learn the different feature maps of the input. From our previous understanding of frame selection in photography, these feature maps also have a different magnitude of importance. This means that some feature maps are more important than others. For example, a feature map containing the edge information might be more important and crucial for learning, compared to another feature map learning background texture transitions. Thus, at a fundamental level, one would want to provide the "more important" feature maps with a higher degree of importance compared to the counterpart feature maps.

This is the foundation for channel attention. We want to focus this "attention" on more important channels, which is basically to give higher importance to specific channels over others. The simplest way to do this by scaling the more important channels by a higher value. This is exactly what Squeeze-Excitation Networks propose.
Squeeze-and-Excitation Networks
In 2018, Hu et al. published their paper titled Squeeze-and-Excitation Networks at CVPR 2018 with a journal version in TPAMI. Hailed to be one of the most influential works in the domain of attention mechanisms, the paper has garnered over 1000 citations. Let's take a look at what the paper proposes.
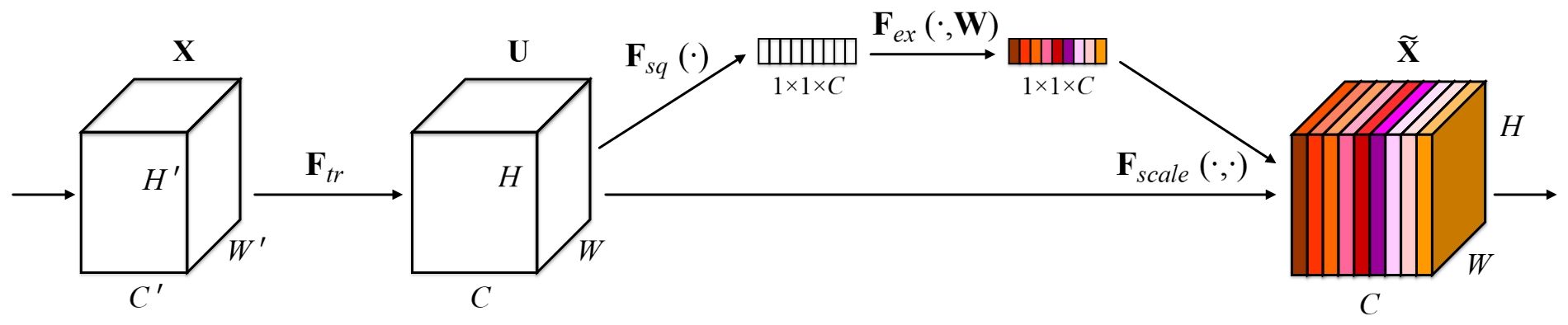
The paper proposes a novel, easy-to-plug-in module called a Squeeze-and-Excite block (abbreviated as SE-block) which consists of three components (shown in the figure above):
- Squeeze Module
- Excitation Module
- Scale Module
Let's go through each of these modules in more details and understand why they're important in the context of channel attention.
Squeeze Module
To obtain optimal channel attention, one would want the scaling of the feature maps to be adaptive to the feature maps themselves. To recap, the feature map set is essentially the output tensor from a convolutional layer (usually a 4-D tensor of dimensionality (B,C,H,W), where the initials represent the Batch size, Channels, Height and Width of the feature maps). For simplicity we will only consider it as a 3-D tensor of the shape (C, H, W)–essentially we are concerned with the depth (number of channels/feature maps in the tensor) and the spatial dimensions of each feature map in that tensor. Thus, to make channel attention adaptive to each channel itself, we have H×W pixels (or values) in total to be concerned with. This would essentially mean that to make the attention truly adaptive, you'd be operating with a total of C×H×W values in total. This value will get very large because in modern neural networks, the number of channels becomes larger with an increasing depth of the network. Thus, the need for using a feature descriptor which can decompose the information of each feature map to a singular value will be helpful in reducing the computational complexity of the whole operation.
This forms the motivation for the Squeeze Module. There exist many feature descriptors which can be used to reduce the spatial dimensions of the feature maps to a singular value, but a general method used for reduction of spatial size in convolutional neural networks is pooling. There are two very popular methods of pooling: Average Pooling and Max Pooling. The former computes the average pixel values within a defined window, while the latter takes the maximum pixel value in the same defined window. Both have their fair share of advantages and disadvantages. While max pooling preserves the most activating pixels, it also can be extremely noisy and won't consider the neighboring pixels. Average pooling, on the other hand, doesn't preserve the information; however, it constructs a smoother average of all the pixels in that window.
The authors did an ablation study to investigate the performance of each descriptor, namely, Global Average Pool (GAP) and Global Max Pool (GMP), which is shown in the following table.
| Descriptor | Top-1 Error Rate | Top-5 Error Rate |
|---|---|---|
| GMP | 22.57 | 6.09 |
| GAP | 22.28 | 6.03 |
The Squeeze Module thus opts for the smoother option of the two, and uses the Global Average Pool (GAP) operation which basically reduces the whole feature map to a singular value by taking the average of all pixels in that feature map. Thus, in terms of dimensionality, if the input tensor is (C×H×W), then after passing it through the GAP operator the output tensor obtained will be of shape (C×1×1), essentially a vector of length C where each feature map is now decomposed to a singular value.
To verify the importance of the Squeeze operator, the authors further compared a Squeeze variant and a No-Squeeze variant, as shown in the following table. Note: a No-Squeeze variant essentially means that the tensor containing the feature maps was not reduced to a single pixel, and the Excitation module operated on the whole tensor.
| Variant | Top-1 Error Rate | Top-5 Error Rate | GFLOPs | Parameters |
|---|---|---|---|---|
| Vanilla ResNet-50 | 23.30 | 6.55 | 3.86 | 25.6M |
| NoSqueeze | 22.93 | 6.39 | 4.27 | 28.1M |
| SE | 22.28 | 6.03 | 3.87 | 28.1M |
Excitation Module
Now with the input tensor decomposed to a considerably smaller size of (C×1×1), the next part of the module is to learn the adaptive scaling weights for these channels. For the Excitation Module in the Squeeze-and-Excitation Block, the authors opt for a fully connected Multi-Layer Perceptron (MLP) bottleneck structure to map the scaling weights. This MLP bottleneck has a single hidden layer along with the input and output layer, which are of the same shape. The hidden layer is used as a reduction block where the input space is reduced to a smaller space defined by the reduction factor (which is set at 16 by default). The compressed space is then expanded back to the original dimensionality as the input tensor. In more compact terms, the changes in dimensionality at every layer of the MLP can be defined by the following three points:
- Input is of shape (C×1×1). Thus, there are C neurons in the input layer.
- Hidden layer reduces this by a reduction factor r, thus leading to a total number of C/r neurons.
- Finally, the output is projected back to the same dimensional space as the input, returning to C neurons in total.
In total, you pass the (C×1×1) tensor as input and obtain a weighted tensor of the same shape–(C×1×1).
The authors provide results for experiments on the performance of a SE module in a ResNet-50 architecture using different reduction ratios (r), as shown in the table below.
| r | Top-1 Error Rate | Top-5 Error Rate | Parameters |
|---|---|---|---|
| 2 | 22.29 | 6.00 | 45.7M |
| 4 | 22.25 | 6.09 | 35.7M |
| 8 | 22.26 | 5.99 | 30.7M |
| 16 | 22.28 | 6.03 | 28.1M |
| 32 | 22.72 | 6.20 | 26.9M |
| Vanilla | 23.30 | 6.55 | 25.6M |
Ideally, for improved information propagation and better cross-channel interaction (CCI), r should be set to 1, thus making it a fully-connected square network with the same width at every layer. However, there exists a trade-off between increasing complexity and performance improvement with decreasing r. Thus, based on the above table, the authors use 16 as the default value for the reduction ratio. This is a hyperparameter with a scope for further tuning to improve upon performance.
Scale Module
After getting the (C×1×1) "excited" tensor from the Excitation Module, it is first passed through a sigmoid activation layer which scales the values to a range of 0-1. Subsequently the output is applied directly to the input by a simple broadcasted element-wise multiplication, which scales each channel/feature map in the input tensor with it's corresponding learned weight from the MLP in the Excitation module.
The authors did further ablation studies on the effect of different non-linear activation functions to be used as the excitation operator, as shown in the following table.
| Activation Function | Top-1 Error Rate | Top-5 Error Rate |
|---|---|---|
| ReLU | 23.47 | 6.98 |
| Tanh | 23.00 | 6.38 |
| Sigmoid | 22.28 | 6.03 |
Based on the results, the authors establish Sigmoid to be the best-performing activation function, and thus employ it as the default excitation operator in the scale module.
To summarize, the Squeeze Excitation Block (SE Block) takes an input tensor x of shape (C×H×W), reduces it to a tensor of shape (C×1×1) by Global Average Pooling (GAP), and subsequently passes this C-length vector into a Multi-Layer Perceptron (MLP) bottleneck structure, and outputs a weighted tensor of the same shape (C×1×1) which is then broadcasted and multiplied element-wise with the input x.
Now, the question is: where is the module "plugged into", e.g. in a Residual Network?
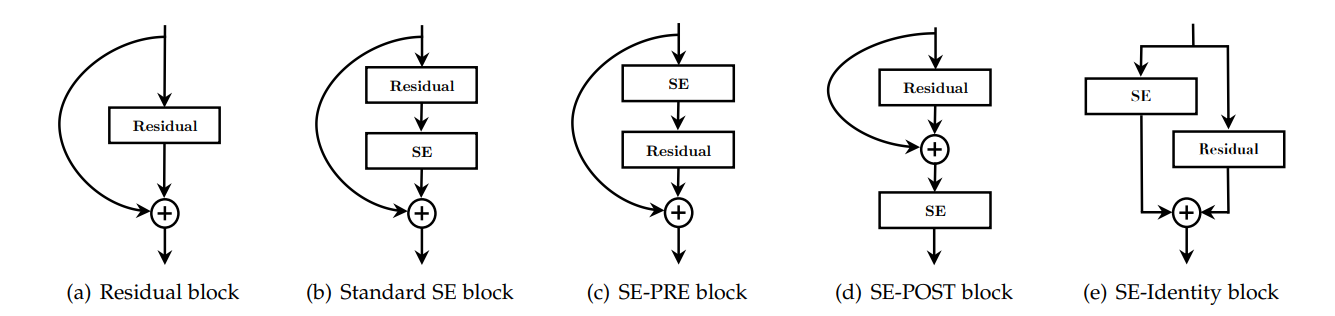
The authors tried out different integration strategies for the SE block, as shown in the above diagram. These include:
- Standard SE
- SE-PRE
- SE-POST
- SE-Identity
The standard SE block is applied right after the final convolutional layer of the architecture, in this case of a Residual Network, right before the merging of the skip connection. The SE-PRE configuration was constructed by placing the SE block at the start of the block, before the first convolutional layer, while SE-POST did the opposite by placing it at the end of the block (after the merging of the skip connection). Finally, the SE-Identity block applied the SE-module in the skip connection branch itself, parallel to the main block, and is added to the final output as a normal residual.
The authors provided the results of their extensive ablation studies on the integration strategies, shown in the following two tables:
Table 1. Effect of different SE Integration Strategy on the error rates of ResNet-50 in ImageNet classification task.
| Strategy | Top-1 Error Rate | Top-5 Error Rate |
|---|---|---|
| SE | 22.28 | 6.03 |
| SE-PRE | 22.23 | 6.00 |
| SE-POST | 22.78 | 6.35 |
| SE-Identity | 22.20 | 6.15 |
Table 2. Effect of introducing SE-block after the spatial 3x3 convolutional layer in a Residual block.
| Design | Top-1 Error Rate | Top-5 Error Rate | GFLOPs | Parameters |
|---|---|---|---|---|
| SE | 22.28 | 6.03 | 3.87 | 28.1M |
| SE-3×3 | 22.48 | 6.02 | 3.86 | 25.8M |
As we can see from the Table 1, every configuration except SE-POST provided a similar and consistent performance. As demonstrated in Table 2, the authors further experimented with inserting the SE-block after the spatial convolution in the residual block. Since the 3×3 spatial convolution has less number of channels, the parameter and FLOPs overhead is much smaller. While it is able to provide similar performance compared to the default SE configuration, the authors didn't provide any conclusive statement on which configuration is most favorable, and kept "SE" as the default integration configuration.
To our fortune, the authors do answer the question of how to integrate SE-blocks into existing architectures.
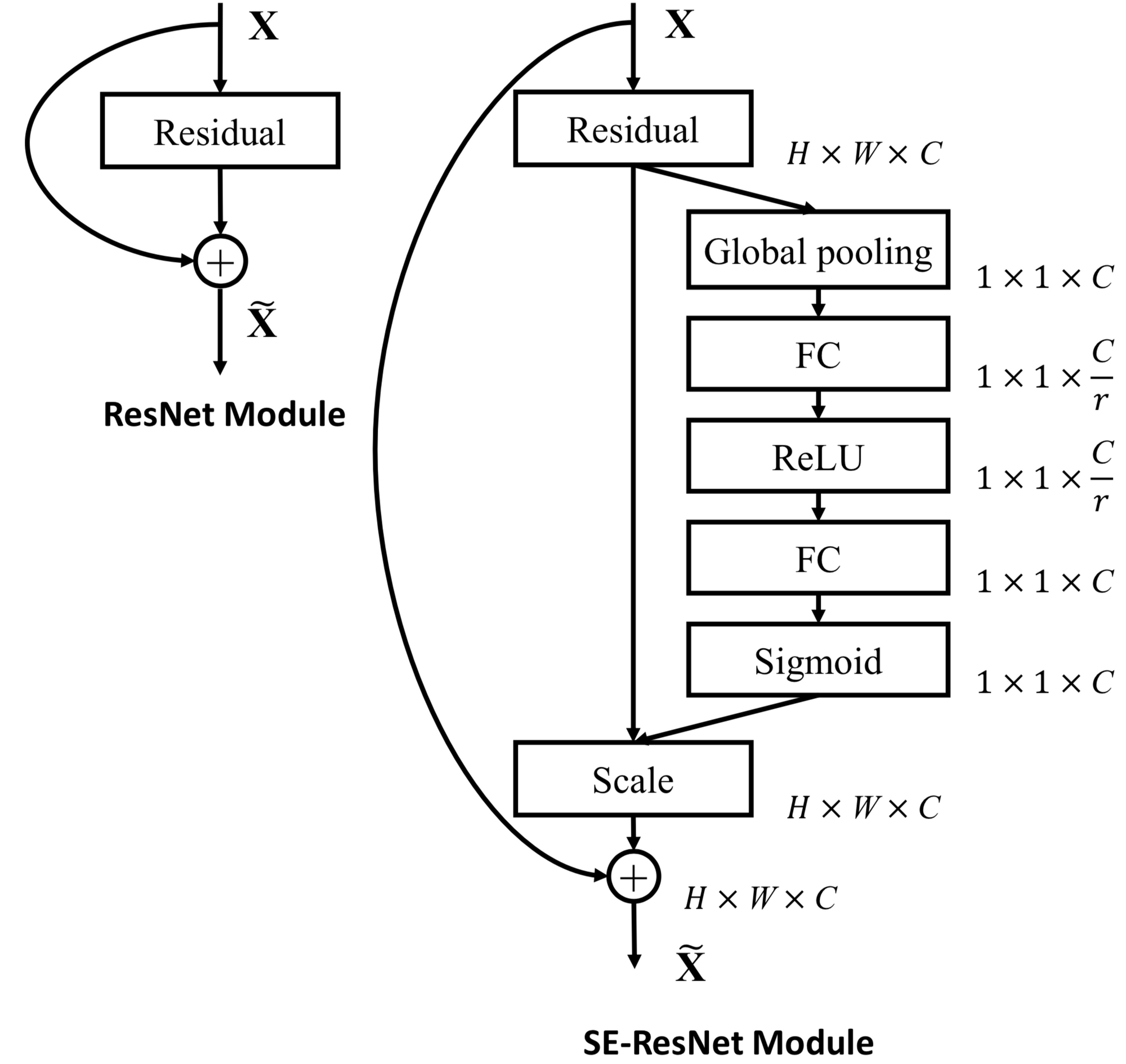
In a Residual Network, the Squeeze-Excitation block is plugged in after the final convolutional layer, in the block prior to the addition of the residual in the skip connection. The intuition behind this is to keep the skip connection branch as clean as possible to make learning the identity easy.
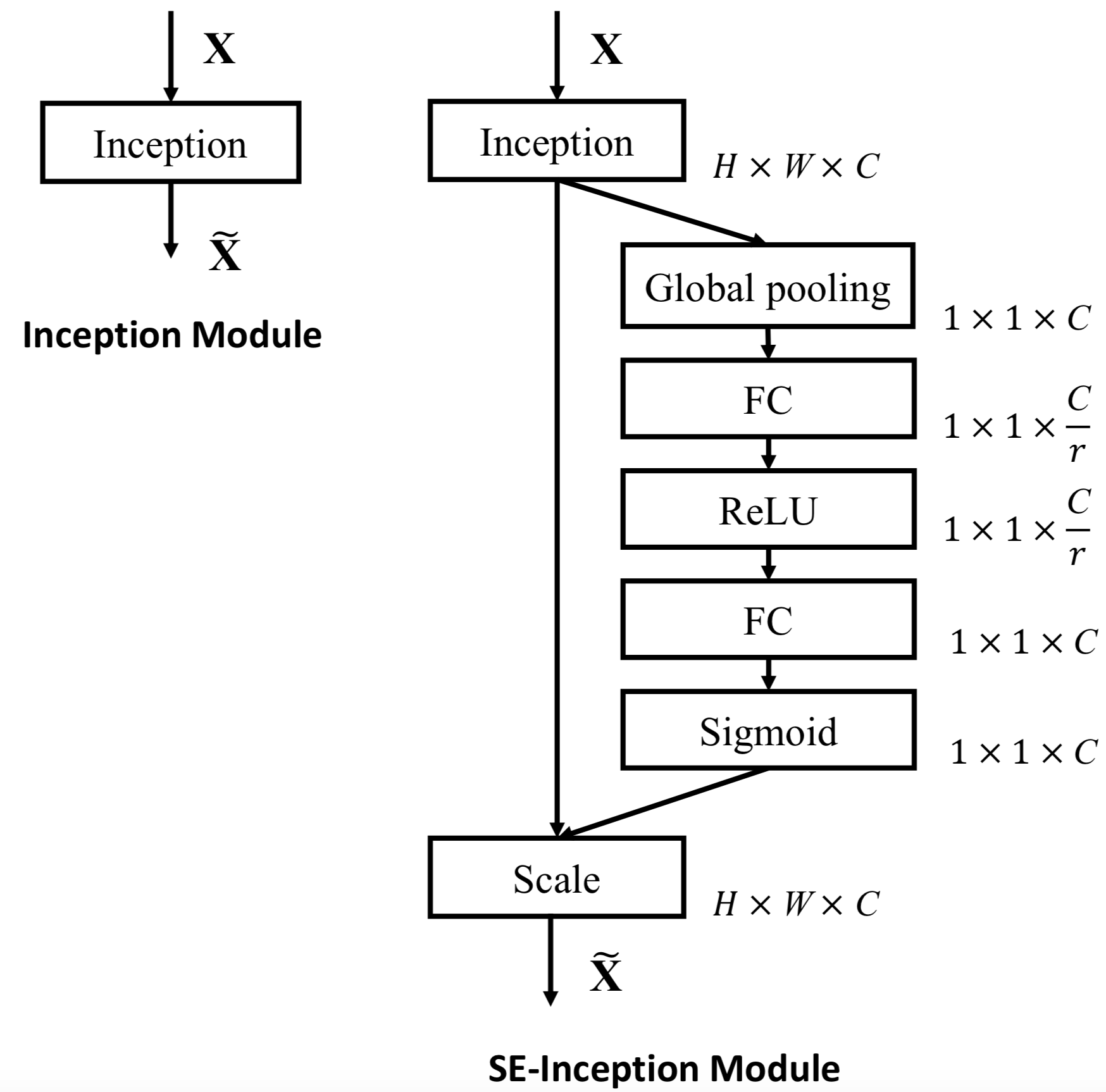
However, in an Inception Network, because of the absence of skip connections, the SE-block is inserted in every Inception block after the final convolutional layer.
In the following figure from the paper, the authors show the modified ResNet-50 and ResNext-50 architectures with an SE-module in every block.
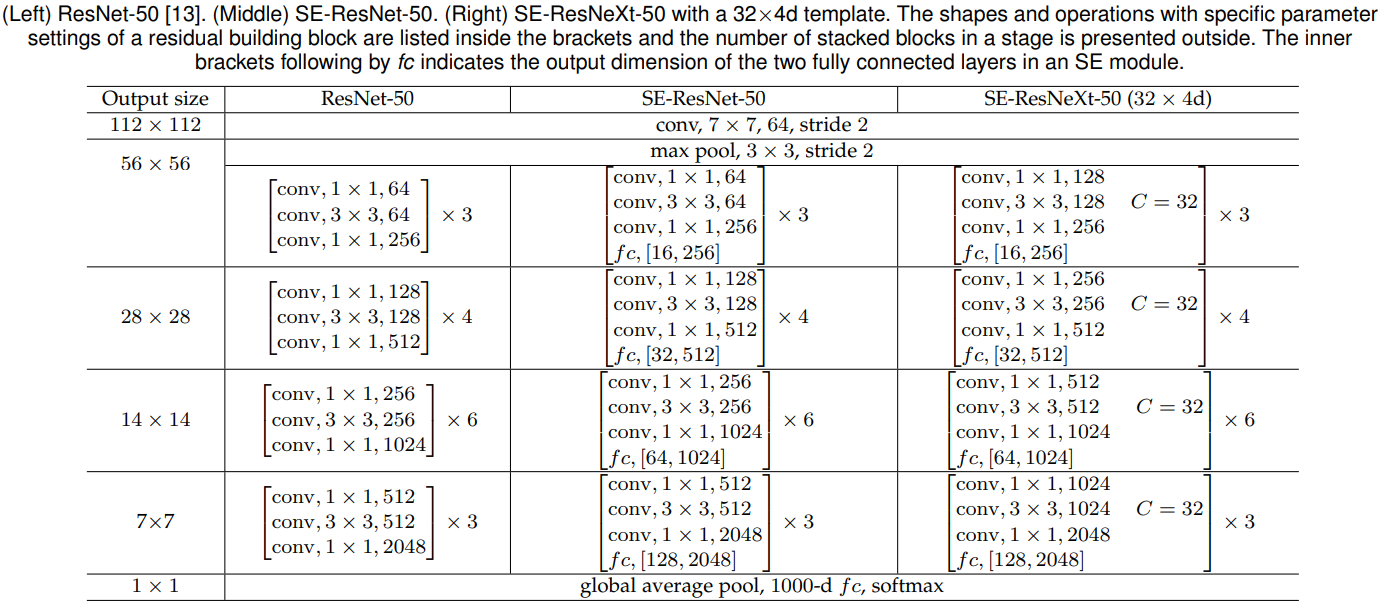
The authors studied extensively the integration strategy of the SE-block in the 4 different stages in a ResNet-50. The results are shown in the following table.
| Stage | Top-1 Error Rate | Top-5 Error Rate | GFLOPs | Parameters |
|---|---|---|---|---|
| ResNet-50 | 23.30 | 6.55 | 3.86 | 25.6M |
| SE Stage 2 | 23.03 | 6.48 | 3.86 | 25.6M |
| SE Stage 3 | 23.04 | 6.32 | 3.86 | 25.7M |
| SE Stage 4 | 22.68 | 6.22 | 3.86 | 26.4M |
| SE All | 22.28 | 6.03 | 3.87 | 28.1M |
Code
The official code repository associated with the paper can be found here. However, the code is structured in Caffe–a less popular framework nowadays. Let's take a look at the PyTorch and TensorFlow versions of the module.
PyTorch
### Import necessary packages
from torch import nn
### Squeeze and Excitation Class definition
class SE(nn.Module):
def __init__(self, channel, reduction_ratio =16):
super(SE, self).__init__()
### Global Average Pooling
self.gap = nn.AdaptiveAvgPool2d(1)
### Fully Connected Multi-Layer Perceptron (FC-MLP)
self.mlp = nn.Sequential(
nn.Linear(channel, channel // reduction_ratio, bias=False),
nn.ReLU(inplace=True),
nn.Linear(channel // reduction_ratio, channel, bias=False),
nn.Sigmoid()
)
def forward(self, x):
b, c, _, _ = x.size()
y = self.gap(x).view(b, c)
y = self.mlp(y).view(b, c, 1, 1)
return x * y.expand_as(x)TensorFlow
import tensorflow as tf
__all__ = [
'squeeze_and_excitation_block',
]
def squeeze_and_excitation_block(input_X, out_dim, reduction_ratio=16, layer_name='SE-block'):
"""Squeeze-and-Excitation (SE) Block
SE block to perform feature recalibration - a mechanism that allows
the network to perform feature recalibration, through which it can
learn to use global information to selectively emphasise informative
features and suppress less useful ones
"""
with tf.name_scope(layer_name):
# Squeeze: Global Information Embedding
squeeze = tf.nn.avg_pool(input_X, ksize=[1, *input_X.shape[1:3], 1], strides=[1, 1, 1, 1], padding='VALID', name='squeeze')
# Excitation: Adaptive Feature Recalibration
## Dense (Bottleneck) -> ReLU
with tf.variable_scope(layer_name+'-variables'):
excitation = tf.layers.dense(squeeze, units=out_dim/reduction_ratio, name='excitation-bottleneck')
excitation = tf.nn.relu(excitation, name='excitation-bottleneck-relu')
## Dense -> Sigmoid
with tf.variable_scope(layer_name+'-variables'):
excitation = tf.layers.dense(excitation, units=out_dim, name='excitation')
excitation = tf.nn.sigmoid(excitation, name='excitation-sigmoid')
# Scaling
scaler = tf.reshape(excitation, shape=[-1, 1, 1, out_dim], name='scaler')
return input_X * scalerMBConv in Efficient Nets
Some of the most influential work which incorporates the Squeeze-Excitation block is that of MobileNet v2 and Efficient Nets, both of which use the mobile inverted residual block (MBConv). Efficient Nets add a Squeeze-Excitation block as well.
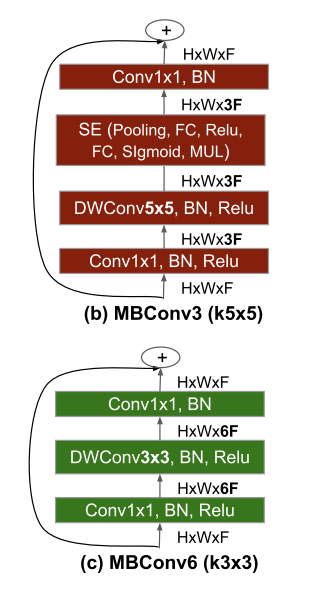
In the MBConv, the Squeeze-Excitation block is placed before the final convolutional layer, after the spatial convolution in the block. This makes it more of an integral part rather than an add-on, for which it was originally intended. The authors of SE-Net had conducted ablation studies and also tested this integration method, however they opted for the default configuration of adding an SE-block after the final 1×1 convolution. Efficient Nets are considered to be state of the art (SOTA) in many tasks, ranging from Image Classification on the standard ImageNet-1k dataset to Object Detection on the MS-COCO dataset. This is a testament to the importance of channel attention, and the efficiency of Squeeze Excitation blocks.
Benchmarks
The authors provide extensive results on different tasks like Image Classification, Scene Classification, and Object Detection, on competitive standard datasets like ImageNet, MS-COCO and Places-365. The following table showcases the efficiency and advantages of using SE modules in the tasks mentioned above:
CIFAR-10 Classification Task
| Architecture | Vanilla | SE-variant |
|---|---|---|
| ResNet-110 | 6.37 | 5.21 |
| ResNet-164 | 5.46 | 4.39 |
| WRN-16-8 | 4.27 | 3.88 |
| Shake-Shake 26 2x96d + Cutout | 2.56 | 2.12 |
The metric used for comparison here is the classification error. The authors also added a form of data augmentation, namely, Cutout in the Shake-Shake network, to confirm whether the performance improvement obtained while using the SE-module is consistent with the usage of different performance-boosting techniques like that of data augmentation.
CIFAR-100 Classification Task
| Architecture | Vanilla | SE-variant |
|---|---|---|
| ResNet-110 | 26.88 | 23.85 |
| ResNet-164 | 24.33 | 21.31 |
| WRN-16-8 | 20.43 | 19.14 |
| Shake-Shake 26 2x96d + Cutout | 15.85 | 15.41 |
ImageNet-1k Classification Task
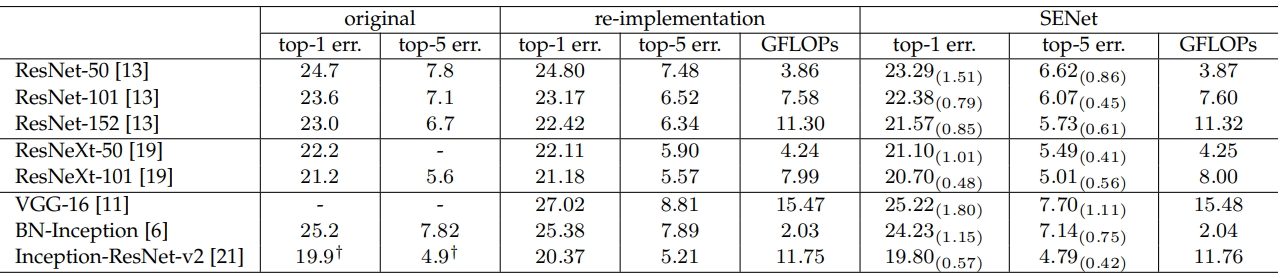

Training Dynamics
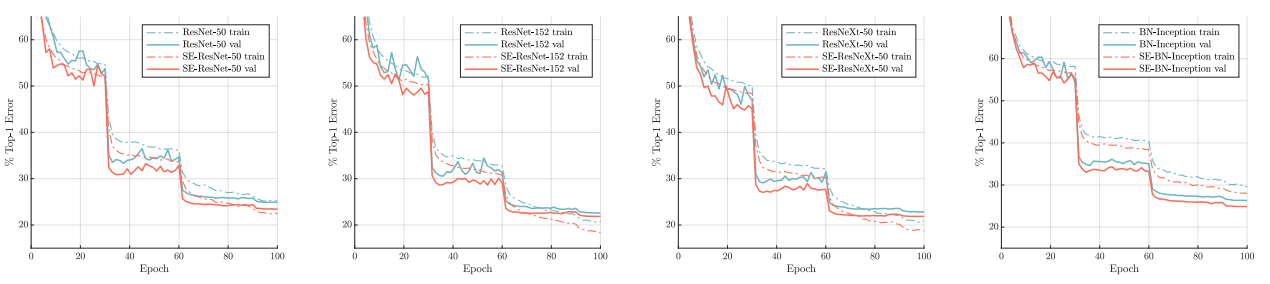
As shown in the graphs above, networks equipped with Squeeze-and-Excitation modules show a consistent improved curve, which thus leads to better generalization and higher performance.
Scene Classification Task on Places-365 Dataset
| Architecture | Top-1 Error Rate | Top-5 Error Rate |
|---|---|---|
| Places-365-CNN | 41.07 | 11.48 |
| ResNet-152 | 41.15 | 11.61 |
| SE-ResNet-152 | 40.37 | 11.01 |
Object Detection Task on MS-COCO Dataset using a Faster RCNN
| Backbone | AP@IoU=0.5 | AP |
|---|---|---|
| ResNet-50 | 57.9 | 38.0 |
| SE-ResNet-50 | 61.0 | 40.4 |
| ResNet-101 | 60.1 | 39.9 |
| SE-ResNet-101 | 62.7 | 41.9 |
Shortcomings
Although the paper is revolutionary in its own right, there are certain outlined flaws in the structure and some inconclusive design strategies.
- The method is quite costly and adds a significant amount of parameters and FLOPS on top of the baseline model. Although in the grand scheme of things this overhead might be very minimal, there have been many new approaches aimed at providing channel attention at an extremely cheap cost which have performed better than SENets, for instance ECANet (published at CVPR 2020).
- Although channel attention seems to be efficient in terms of parameters and FLOPs overhead, one major flaw is the scaling operation where the weighted channel vector is broadcasted and applied/multiplied element-wise to the input tensor. This intermediate broadcasted tensor is of the same dimensional space as that of the input, causing an increase in memory complexity by a large margin. This renders the training process slower and more memory-intensive.
- To reduce computational complexity there exists a bottleneck structure in the MLP of the excitation module of the block, where the number of channels are reduced by a specified reduction ratio. This causes information loss and is thus sub-optimal.
- Since SENet only revolves around providing channel attention by using dedicated global feature descriptors, which in this case is Global Average Pooling (GAP), there is a loss of information and the attention provided is point-wise. This means that all pixels are mapped in the spatial domain of a feature map uniformly, and thus not discriminating between important or class-deterministic pixels versus those which are part of the background or not containing useful information. Thus, the importance/need for spatial attention is justified to be coupled with channel attention. One of the prime examples of the same is CBAM (published at ECCV 2018).
- There are inconclusive design strategies regarding SENet. The authors stated that this is beyond the scope of the paper to understand what the optimal setting would be, which includes the positional integration strategy for SE modules and the reduction ratio to be used in the MLP.











