Introduced in the paper, An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale, Vision Transformers (ViT) are the new talk of the town for SOTA image classification. Experts feel this is only the tip of the iceberg when it comes to Transformer architectures replacing their convolutional counterparts for upstream/downstream tasks.
An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale https://t.co/r5a0RuWyZE v cool. Further steps towards deprecating ConvNets with Transformers. Loving the increasing convergence of Vision/NLP and the much more efficient/flexible class of architectures. pic.twitter.com/muj3cR6uGA
— Andrej Karpathy (@karpathy) October 3, 2020
Here, I break down the inner workings of the Vision Transformer.
Bring this project to life
Attention
Before I get into the specifics of ViT, let me break down what the Attention mechanism is and how it works. You can skip this part if you already know this.
Self Attention is an important concept re-introduced in the paper, Attention Is All You Need. It enables sequence learners to better understand the relationship between different tokens in the sequences they are training on. For a given sequence, when a certain token attends to another, it means they are closely related and have an impact on each other in the context of the whole sequence.
For example, in the sentence "The horse walked on the bridge", "across" will probably attend to "bridge" and "horse" since it establishes the context of the sentence. The "horse" is the entity that's walking across, and the "bridge" is the object being walked across. Through pre-training, these relationships are learned and enforced.
Let's break down this process of running Self Attention on a collection of sequences.
- For a given sequence, the $m$ incoming word vectors of length $n$ are stacked and multiplied by an initial set of weights $W_q$, $W_k$, and $W_v$, of dimensions $n \times D$ – this gives us 3 matrices, queries $Q$, keys $K$, and values $V$, of size $m \times D$. Here, $D$ is the embedding dimension used throughout the Transformer.
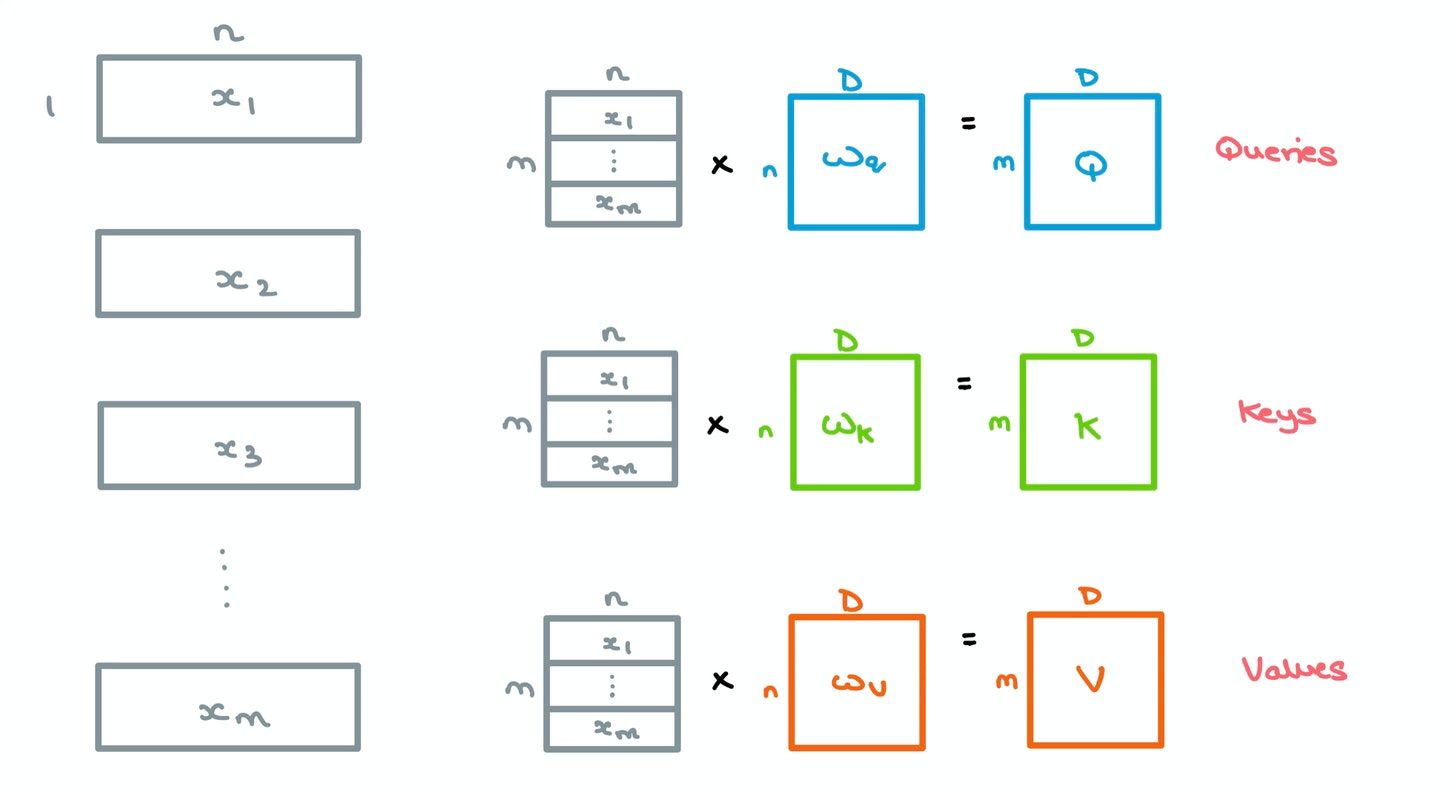
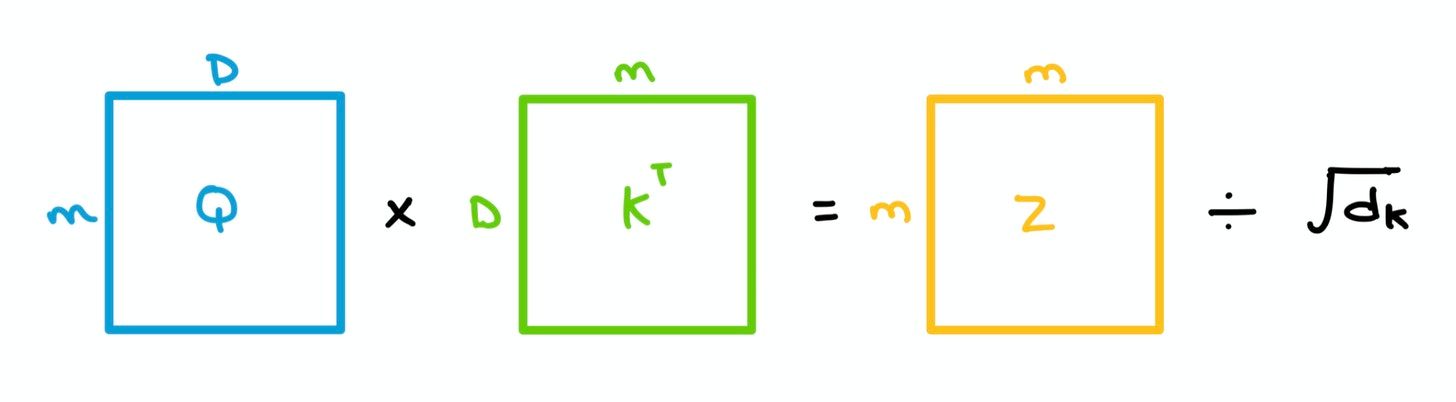
- A dot product is taken between each query $q$ from $Q$ and all the keys $k$ in $K$ collectively – in linear algebra terms, this means we simply multiply $Q$ and the transpose of $K$. This gives us a $m \times m$ matrix which we divide by the square root of the dimension of $K$ (64 in the paper) to give us Attention matrix $Z$.
This is called Scaled Dot Product Attention, and it's used to prevent exploding/vanishing gradients.
Without scaling, the dot product grows in magnitude, pushing the Softmax values to regions where gradients are really small during Backpropagation.
- The Softmax of the $m \times m$ matrix $Z$ is taken to give us the Attention weights; it tells us which set of tokens in the sequence attend to one another. This resulting matrix is multiplied with $V$ to give us the final Self Attention outputs.
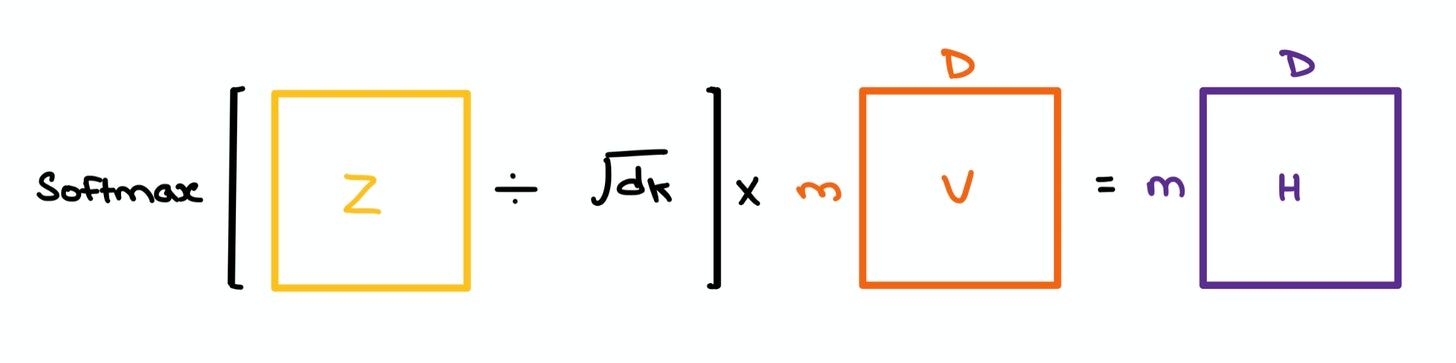
The "Self" in Self Attention comes from the fact that we're comparing the tokens in a sequence with every other token in the same sequence. If a sequence has 5 token vectors, the resulting Attention matrix will have 5x5 entries depicting the relationships between each word with the other words.
This is why Self Attention is said to have Quadratic complexity.
Multi-Headed Self Attention
You can think of each head as an independent "box" performing the 3 operations mentioned above. Each box comes up with its own set of independent weights $W_q$, $W_k$, and $W_v$, but takes in the same sequence $X$.
We do this to increase the predictive power of the Transformer since each head has its own internal representation of the inputs; it allows for a more complete understanding of the relationships between words in a sequence (i.e., collective, shared knowledge). Any relationship information missed by one head is highly likely to be aptured in another head.
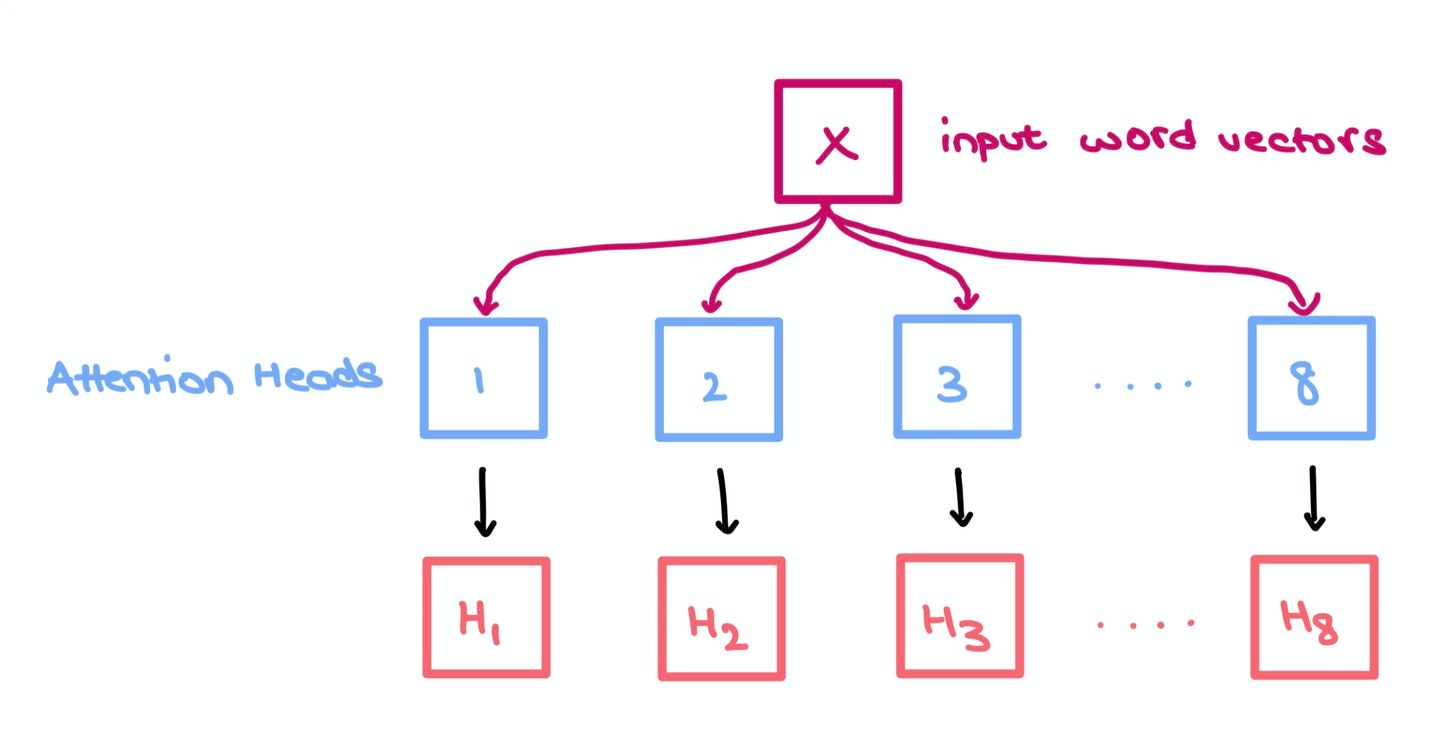
Like in the paper, suppose we have 8 heads. We simply concatenate them to give us an $m \times m \times 8$ tensor which we multiply with another set of weights $W_o$ of size $8 \times D \times J$ to give us a $m \times J$ matrix.
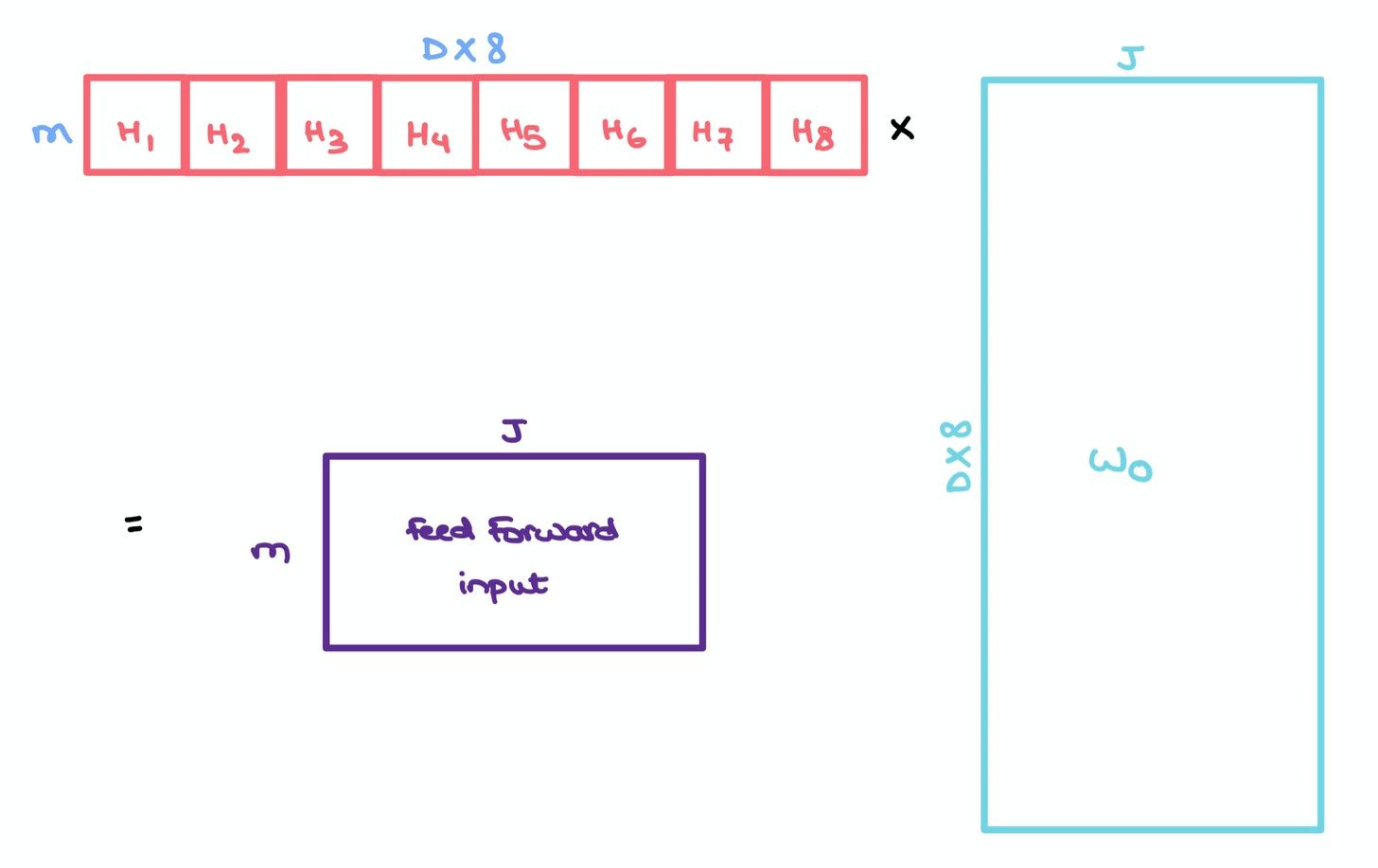
This resulting matrix captures the information of all the heads and can be sent to a Feed Forward layer with hidden layer $J$ for further processing.
Encoder Block
Multi-headed Self-Attention, LayerNorm, and Feed Forward layers are used to form a single Encoder Block as shown below. The original paper makes use of Residual Skip Connections that route information between disconnected layers.
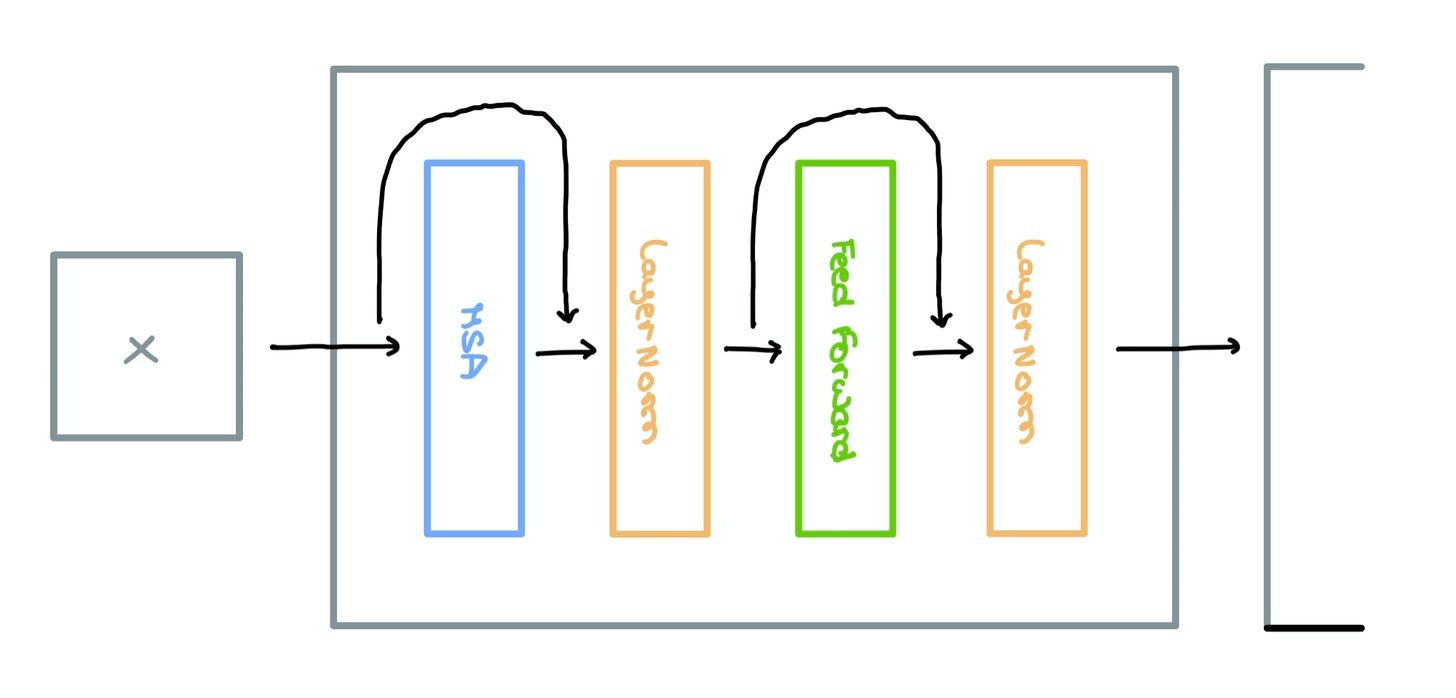
To find out more about the benefits of adding Skip Connections, check out this article.
Encoder
These Encoder Blocks are stacked one top of each other to form the Encoder architecture; the paper suggests stacking 6 of these blocks. Sequences are converted into word vectors and sent in for encoding.
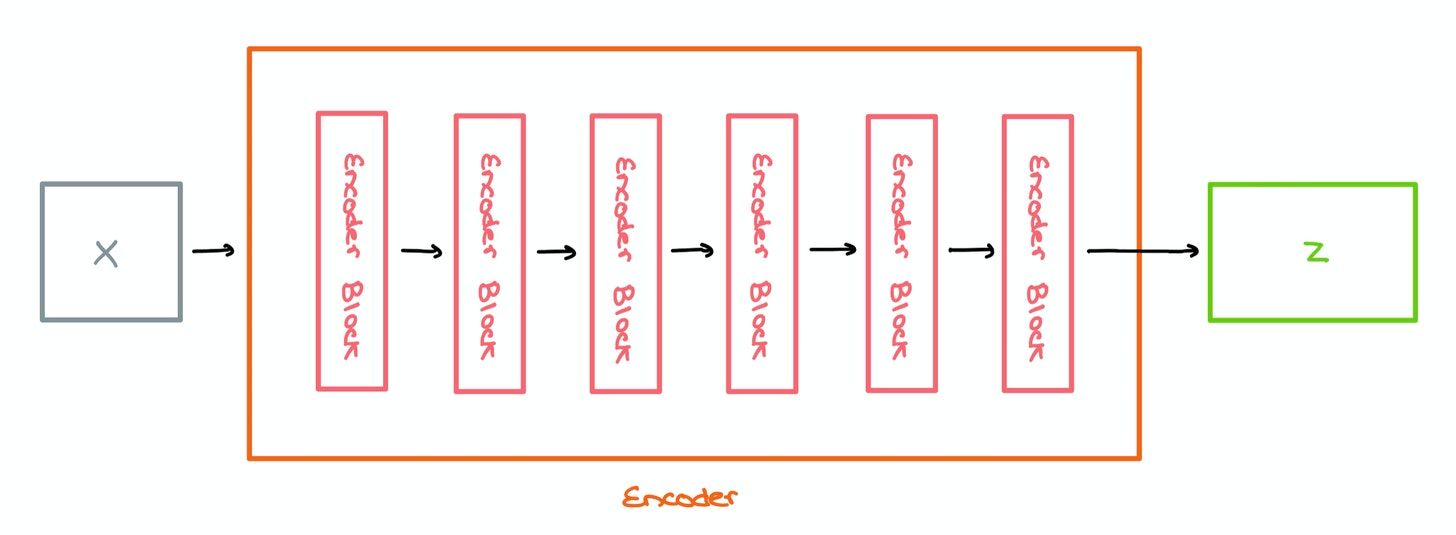
In a regular Transformer, the output Z of the Encoder is sent into the Decoder (not covered here). However, in the ViT, it’s sent into a Multilayer Perceptron for classification.
For a complete breakdown of Transformers with code, check out Jay Alammar’s Illustrated Transformer.
Vision Transformer
Now that you have a rough idea of how Multi-headed Self-Attention and Transformers work, let’s move on to the ViT. The paper suggests using a Transformer Encoder as a base model to extract features from the image, and passing these “processed” features into a Multilayer Perceptron (MLP) head model for classification.
Processing Images
Transformers are already very compute-heavy – they’re infamous for their quadratic complexity when computing the Attention matrix. This worsens as the sequence length increases.
For the sake of simplicity, I’m assuming we’re working with a grayscale image with only one color channel. The same principle works with multiple channels (like RGB) – the only thing changing is the patch dimensions from $P \times P$ to $P \times P \times C$, where $C$ is the number of channels.
For a standard $28 \times 28$ MNIST image, we’d have to deal with 784 pixels. If we were to pass this flattened vector of length 784 through the Attention mechanism, we’d then obtain a $784 \times 784$ Attention Matrix to see which pixels attend to one another. This is very costly even for modern-day hardware.
This is why the paper suggests breaking the image down into square patches as a form of lightweight “windowed” Attention.
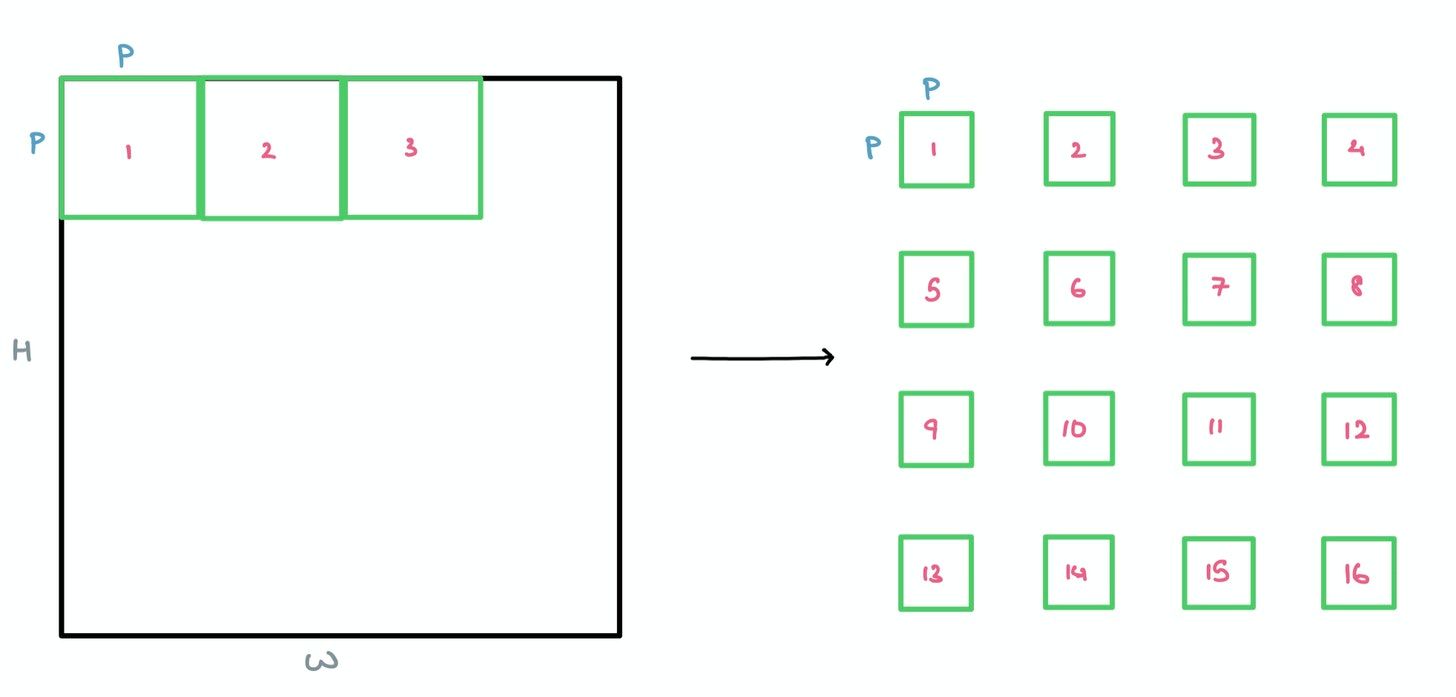
These patches are then flattened and sent through a single Feed Forward layer to get a linear patch projection. This Feed Forward layer contains the embedding matrix $E$ as mentioned in the paper. This matrix $E$ is randomly generated.
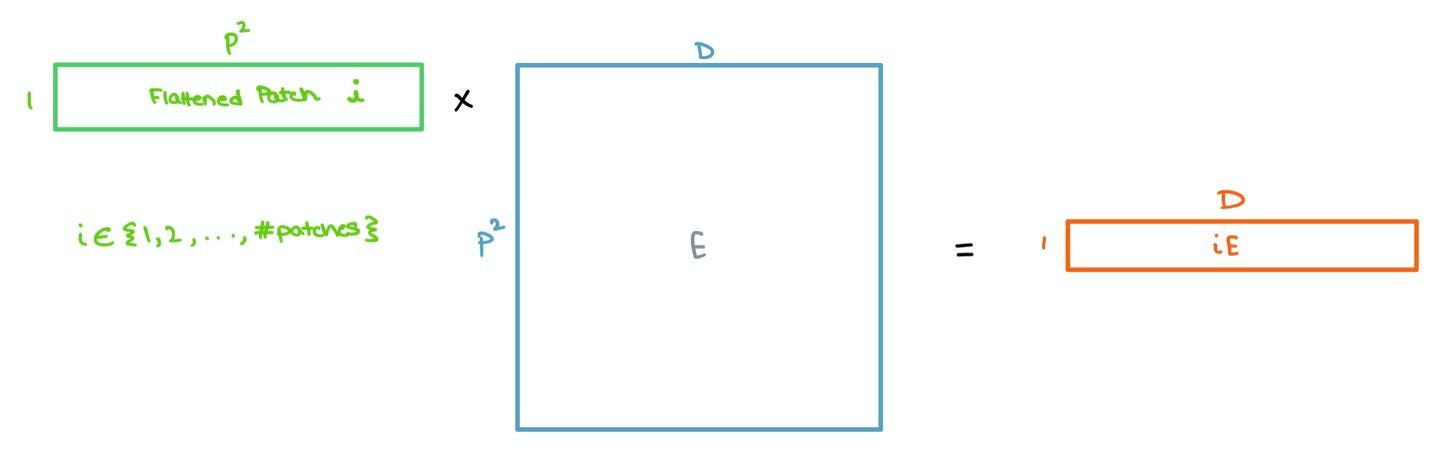
To help with the classification bit, the authors took inspiration from the original BERT paper by concatenating a learnable [class] embedding with the other patch projections. This learnable embedding will be important at a later stage, which we’ll get to soon.
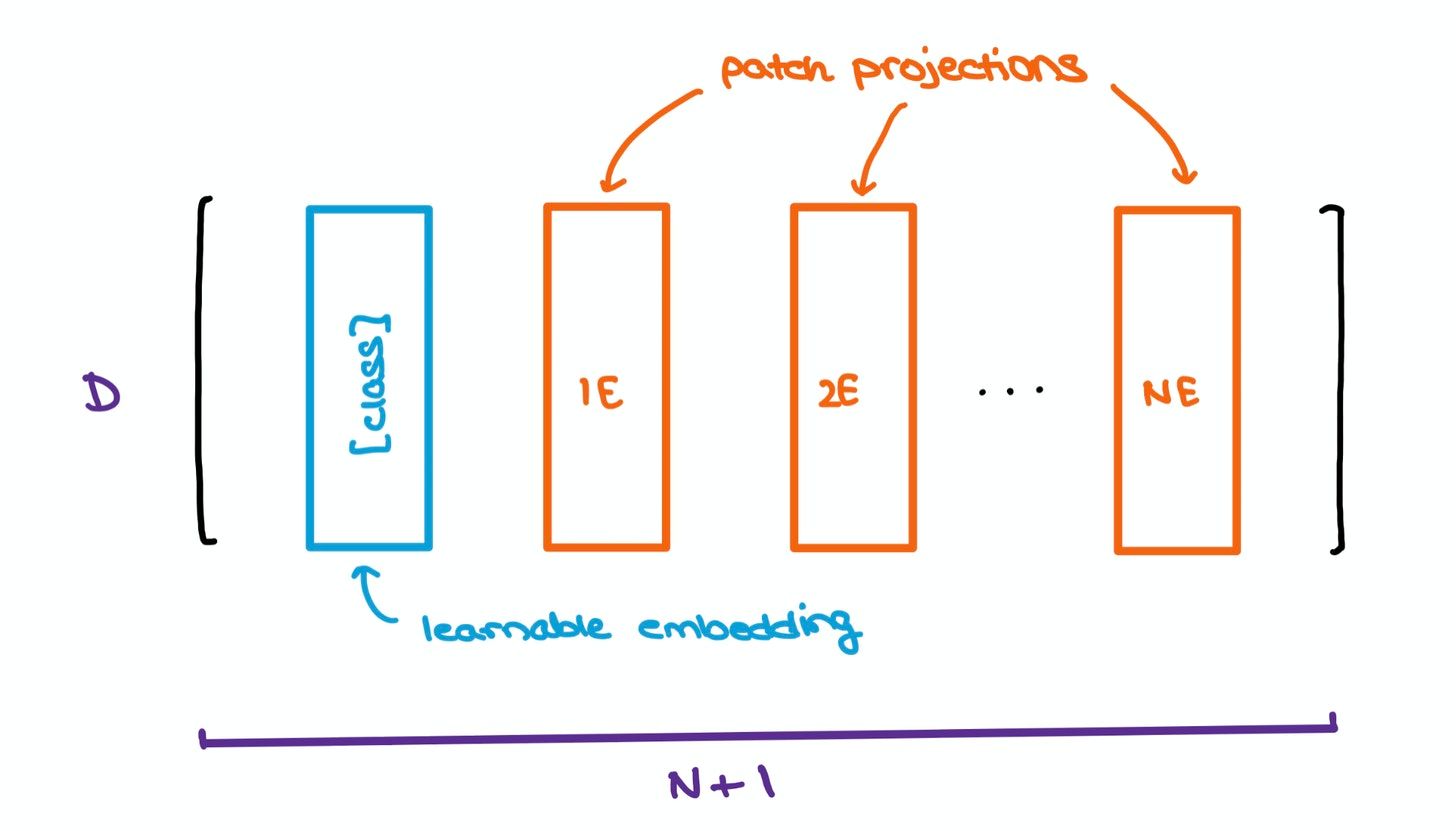
Yet another problem with Transformers is that the order of a sequence is not enforced naturally since data is passed in at a shot, instead of timestep-wise, as is done in RNNs and LSTMs. To combat this, the original Transformer paper suggests using Positional Encodings/Embeddings that establish a certain order in the inputs.
The positional embedding matrix $E_{\text{pos}}$ is also randomly generated and added to the concatenated matrix containing the learnable class embedding and patch projections.
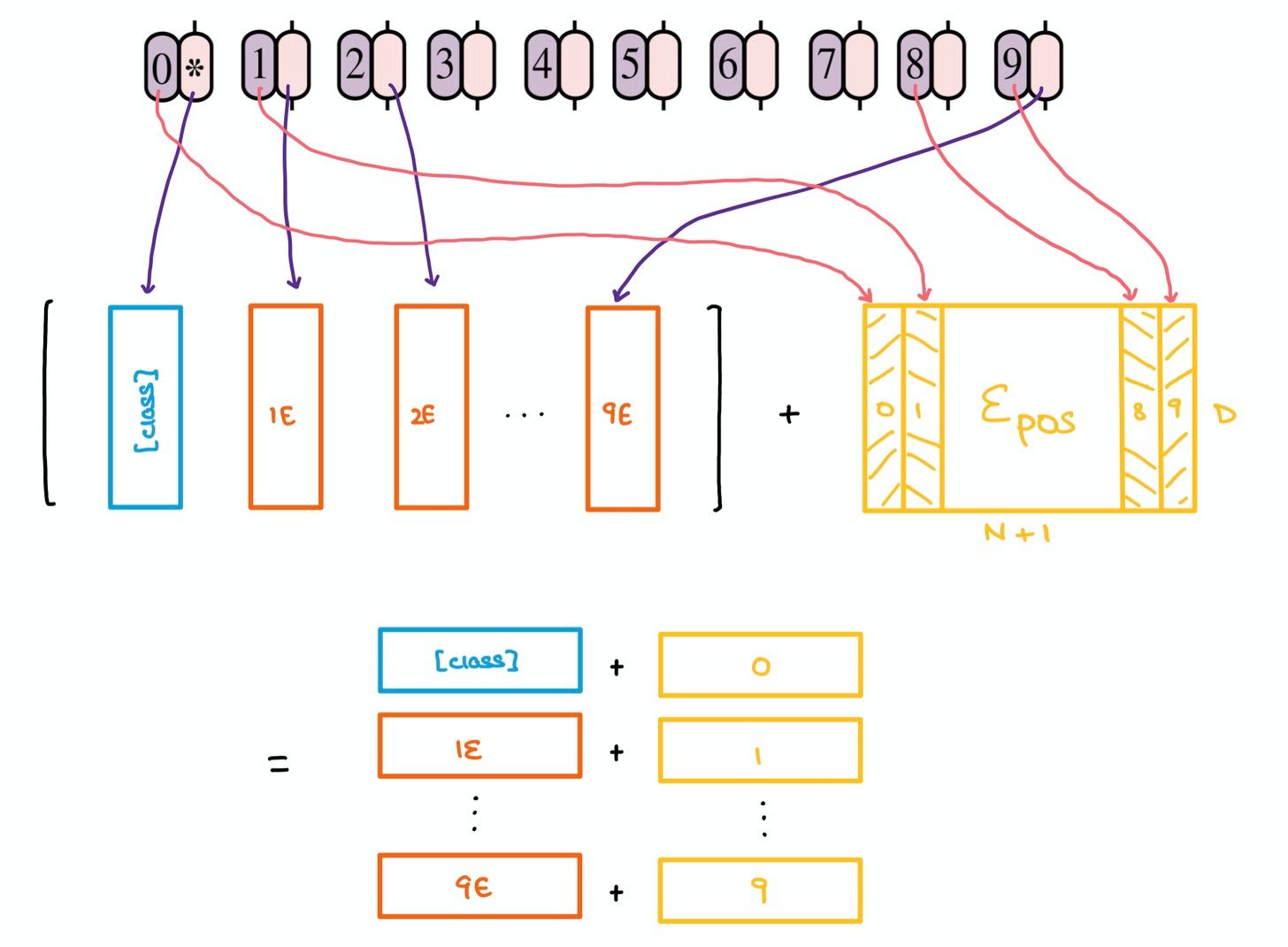
Altogether, these patch projections and positional embeddings form a larger matrix that’ll soon be put through the Transformer Encoder.
MLP Head
The outputs of the Transformer Encoder are then sent into a Multilayer Perceptron for image classification. The input features capture the essence of the image very well, hence making the MLP head’s classification task far simpler.
The Transformer gives out multiple outputs. Only the one related to the special [class] embedding is fed into the classification head; the other outputs are ignored. The MLP, as expected, outputs a probability distribution of the classes the image could belong to.
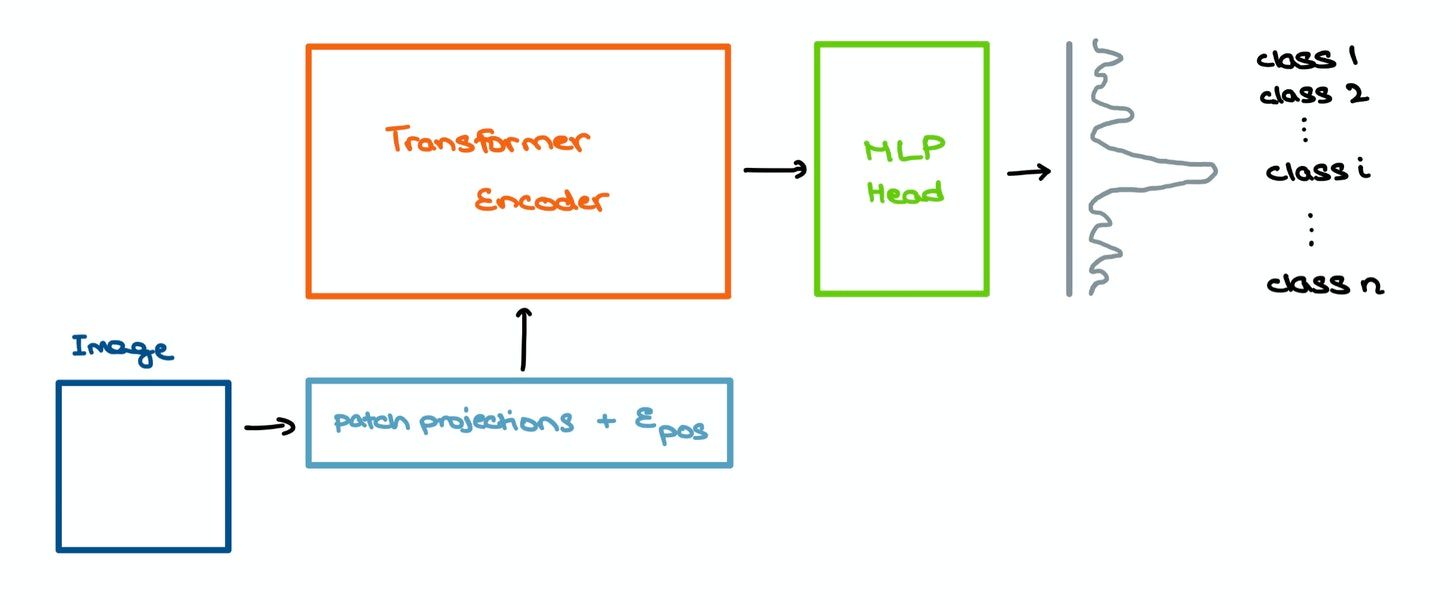
[class] embedding and ignores the other outputs.In a nutshell
The Vision Transformer paper was among my favorite submissions to ICLR 2021. It was a fairly simple model that came with promise.
It achieved some SOTA benchmarks on trending image classification datasets like Oxford-IIIT Pets, Oxford Flowers, and Google Brain’s proprietary JFT-300M after pre-training on ILSVRC’s ImageNet and its superset ImageNet-21M.
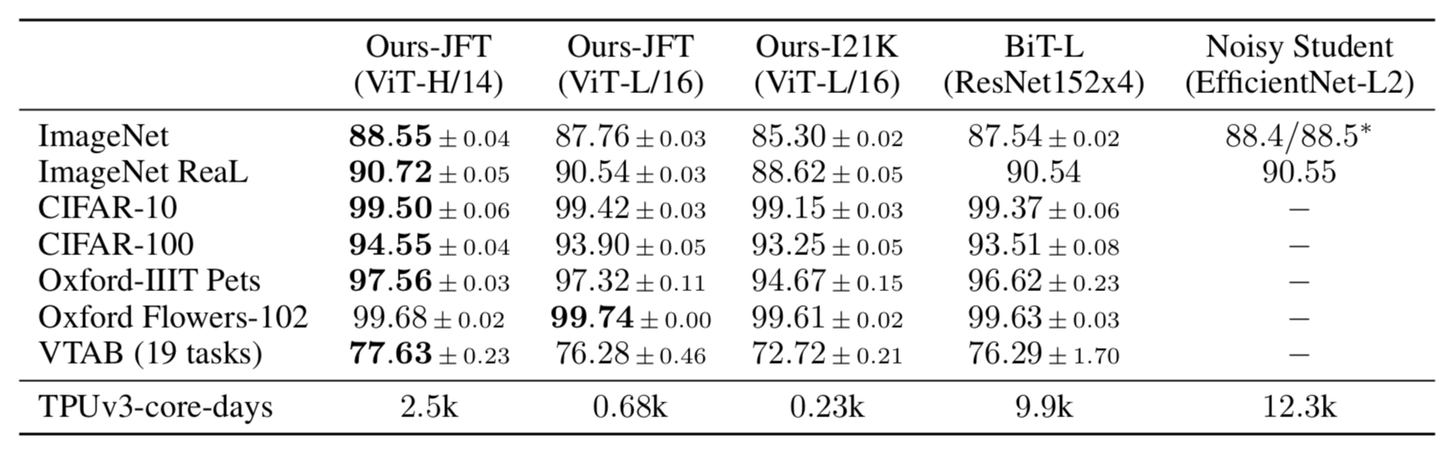
In the Visual Task Adaptation Benchmark (VTAB), it achieves some decent scores in different (challenging) categories.
Transformers aren’t mainstream yet
Sure, these scores are great. Although I, like many others, still believe we’re far from a reality where Transformers perform most up/downstream tasks. Their operations are compute-heavy, training takes ages on decent hardware, and the final trained model is too large to host on hacky servers (for projects, at least) without severe latency issues during inference. It has its shortcomings that have to be dealt with before becoming the convention in industry applications.
Yet, this is just the beginning; I’m sure there’ll be tons of research in this area to make Transformer architectures more efficient and lightweight. Till then, we’ve got to keep swimming.
Thanks for reading! I’ll catch you in the next one.











