Bring this project to life
This article is about one of the best GANs today, StyleGAN from the paper A Style-Based Generator Architecture for Generative Adversarial Networks, we will make a clean, simple, and readable implementation of it using PyTorch, and try to replicate the original paper as closely as possible, so if you read the paper, the implementation should be pretty much identical.
If you don't read the StyleGAN1 paper or don't know how it works and you want to understand it, I highly recommend you to check out this blog post where I go through the details of it.
The dataset that we will use in this blog is this dataset from Kaggle which contains 16240 upper clothes for women with 256*192 resolution.
Load all dependencies we need
We first will import torch since we will use PyTorch, and from there we import nn. That will help us create and train the networks, and also let us import optim, a package that implements various optimization algorithms (e.g. sgd, adam,..). From torchvision we import datasets and transforms to prepare the data and apply some transforms.
We will import functional as F from torch.nn to upsample the images using interpolate, DataLoader from torch.utils.data to create mini-batch sizes, save_image from torchvision.utils to save some fake samples, and log2 form math because we need the inverse representation of the power of 2 to implement the adaptive minibatch size depending on the output resolution, NumPy for linear algebra, os for interaction with the operating system, tqdm to show progress bars, and finally matplotlib.pyplot to show the results and compare them with the real ones.
import torch
from torch import nn, optim
from torchvision import datasets, transforms
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision.utils import save_image
from math import log2
import numpy as np
import os
from tqdm import tqdm
import matplotlib.pyplot as plt
Hyperparameters
- Initialize the DATASET by the path of the real images.
- Specify the start train at image size 8x8.
- Initialize the device by Cuda if it is available and CPU otherwise, and learning rate by 0.001.
- The batch size will be different depending on the resolution of the images that we want to generate, so we initialize BATCH_SIZES by a list of numbers, you can change them depending on your VRAM.
- Initialize image_size by 128 and CHANNELS_IMG by 3 because we will generate 128 by 128 RGB images.
- In the original paper, they initialize Z_DIM, W_DIM, and IN_CHANNELS by 512, but I initialize them by 256 instead for less VRAM usage and speed-up training. We could perhaps even get better results if we doubled them.
- For StyleGAN we can use any of the GANs loss functions we want, so I use WGAN-GP from the paper Improved Training of Wasserstein GANs. This loss contains a parameter name λ and it's common to set λ = 10.
- Initialize PROGRESSIVE_EPOCHS by 30 for each image size.
DATASET = "Women clothes"
START_TRAIN_AT_IMG_SIZE = 8 #The authors start from 8x8 images instead of 4x4
DEVICE = "cuda" if torch.cuda.is_available() else "cpu"
LEARNING_RATE = 1e-3
BATCH_SIZES = [256, 128, 64, 32, 16, 8]
CHANNELS_IMG = 3
Z_DIM = 256
W_DIM = 256
IN_CHANNELS = 256
LAMBDA_GP = 10
PROGRESSIVE_EPOCHS = [30] * len(BATCH_SIZES)Get data loader
Now let's create a function get_loader to:
- Apply some transformation to the images (resize the images to the resolution that we want, convert them to tensors, then apply some augmentation, and finally normalize them to be all the pixels ranging from -1 to 1).
- Identify the current batch size using the list BATCH_SIZES, and take as an index the integer number of the inverse representation of the power of 2 of image_size/4. And this is actually how we implement the adaptive minibatch size depending on the output resolution.
- Prepare the dataset by using ImageFolder because it's already structured in a nice way.
- Create mini-batch sizes using DataLoader that take the dataset and batch size with shuffling the data.
- Finally, return the loader and dataset.
def get_loader(image_size):
transform = transforms.Compose(
[
transforms.Resize((image_size, image_size)),
transforms.ToTensor(),
transforms.RandomHorizontalFlip(p=0.5),
transforms.Normalize(
[0.5 for _ in range(CHANNELS_IMG)],
[0.5 for _ in range(CHANNELS_IMG)],
),
]
)
batch_size = BATCH_SIZES[int(log2(image_size / 4))]
dataset = datasets.ImageFolder(root=DATASET, transform=transform)
loader = DataLoader(
dataset,
batch_size=batch_size,
shuffle=True,
)
return loader, dataset
Models implementation
Now let's Implement the StyleGAN1 generator and discriminator(ProGAN and StyleGAN1 have the same discriminator architecture) with the key attributions from the paper. We will try to make the implementation compact but also keep it readable and understandable. Specifically, the key points:
- Noise Mapping Network
- Adaptive Instance Normalization (AdaIN)
- Progressive growing
In this tutorial, we will just generate images with StyleGAN1, and not implement style mixing and stochastic variation, but it shouldn't be hard to do so.
Let's define a variable with the name factors that contain the numbers that will multiply with IN_CHANNELS to have the number of channels that we want in each image resolution.
factors = [1, 1, 1, 1, 1 / 2, 1 / 4, 1 / 8, 1 / 16, 1 / 32]Noise Mapping Network
The noise mapping network takes Z and puts it through eight fully connected layers separated by some activation. And don't forget to equalize the learning rate as the authors do in ProGAN (ProGAN and StyleGan authored by the same researchers).
Let's first build a class with the name WSLinear (weighted scaled Linear) which will be inherited from nn.Module.
- In the init part we send in_features and out_channels. Create a linear layer, then we define a scale that will be equal to the square root of 2 divided by in_features, we copy the bias of the current column layer into a variable because we don't want the bias of the linear layer to be scaled, then we remove it, Finally, we initialize linear layer.
- In the forward part, we send x and all that we are going to do is multiplicate x with scale and add the bias after reshaping it.
class WSLinear(nn.Module):
def __init__(
self, in_features, out_features,
):
super(WSLinear, self).__init__()
self.linear = nn.Linear(in_features, out_features)
self.scale = (2 / in_features)**0.5
self.bias = self.linear.bias
self.linear.bias = None
# initialize linear layer
nn.init.normal_(self.linear.weight)
nn.init.zeros_(self.bias)
def forward(self, x):
return self.linear(x * self.scale) + self.biasNow let's create the MappingNetwork class.
- In the init part we send z_dim and w_din, and we define the network mapping that first normalizes z_dim, followed by eight of WSLInear and ReLU as activation functions.
- In the forward part, we return the network mapping.
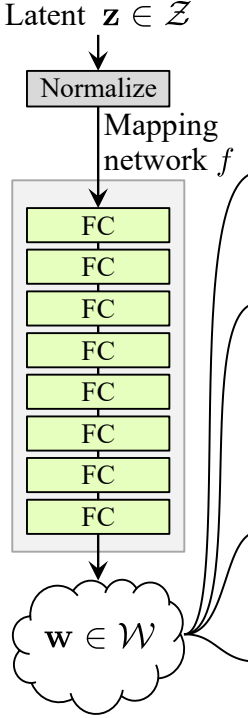
class MappingNetwork(nn.Module):
def __init__(self, z_dim, w_dim):
super().__init__()
self.mapping = nn.Sequential(
PixelNorm(),
WSLinear(z_dim, w_dim),
nn.ReLU(),
WSLinear(w_dim, w_dim),
nn.ReLU(),
WSLinear(w_dim, w_dim),
nn.ReLU(),
WSLinear(w_dim, w_dim),
nn.ReLU(),
WSLinear(w_dim, w_dim),
nn.ReLU(),
WSLinear(w_dim, w_dim),
nn.ReLU(),
WSLinear(w_dim, w_dim),
nn.ReLU(),
WSLinear(w_dim, w_dim),
)
def forward(self, x):
return self.mapping(x)Adaptive Instance Normalization (AdaIN)
Now let's create AdaIN class
- In the init part we send channels, w_dim, and we initialize instance_norm which will be the instance normalization part, and we initialize style_scale and style_bias which will be the adaptive parts with WSLinear that maps the Noise Mapping Network W into channels.
- In the forward pass, we send x, apply instance normalization for it, and return style_sclate * x + style_bias.
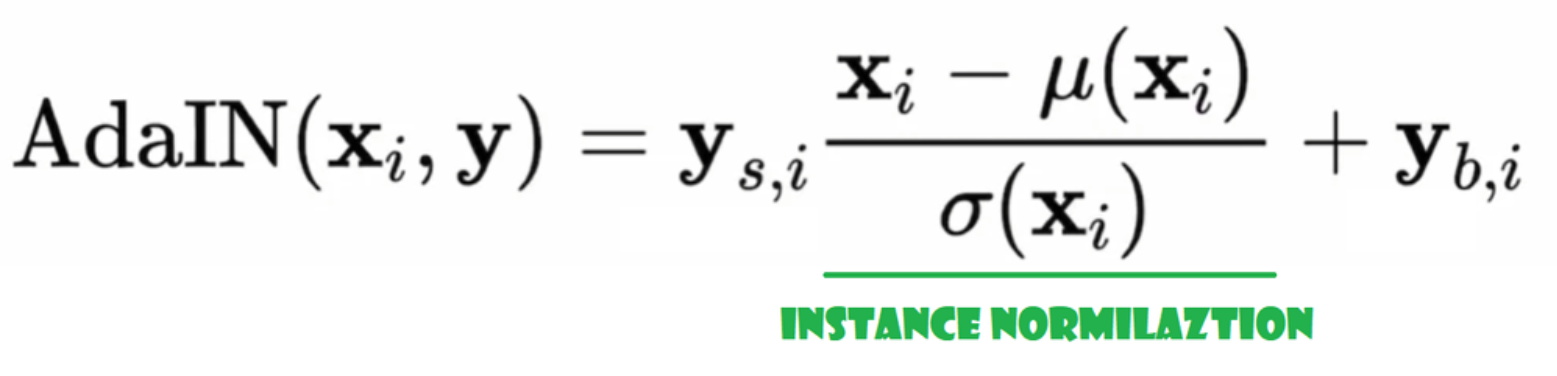
class AdaIN(nn.Module):
def __init__(self, channels, w_dim):
super().__init__()
self.instance_norm = nn.InstanceNorm2d(channels)
self.style_scale = WSLinear(w_dim, channels)
self.style_bias = WSLinear(w_dim, channels)
def forward(self, x, w):
x = self.instance_norm(x)
style_scale = self.style_scale(w).unsqueeze(2).unsqueeze(3)
style_bias = self.style_bias(w).unsqueeze(2).unsqueeze(3)
return style_scale * x + style_biasInject Noise
Now let's create the class InjectNoise to inject the noise into the generator
- In the init part we sent channels and we initialize weight from a random normal distribution and we use nn.Parameter so that these weights can be optimized
- In the forward part, we send an image x and we return it with random noise added
class InjectNoise(nn.Module):
def __init__(self, channels):
super().__init__()
self.weight = nn.Parameter(torch.zeros(1, channels, 1, 1))
def forward(self, x):
noise = torch.randn((x.shape[0], 1, x.shape[2], x.shape[3]), device=x.device)
return x + self.weight * noisehelpful classes
The authors build StyleGAN upon the official implementation of ProGAN by Karras et al, they use the same discriminator architecture, adaptive minibatch size, hyperparameters, etc. So there are a lot of classes that stay the same from ProGAN implementation.
In this section, we will create the classes that do not change from the ProGAN architecture that I have already explained in this post blog.
In the code snippet below you can find the class WSConv2d (weighted scaled convolutional layer) to Equalized Learning Rate for the conv layers.
class WSConv2d(nn.Module):
def __init__(
self, in_channels, out_channels, kernel_size=3, stride=1, padding=1
):
super(WSConv2d, self).__init__()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding)
self.scale = (2 / (in_channels * (kernel_size ** 2))) ** 0.5
self.bias = self.conv.bias
self.conv.bias = None
# initialize conv layer
nn.init.normal_(self.conv.weight)
nn.init.zeros_(self.bias)
def forward(self, x):
return self.conv(x * self.scale) + self.bias.view(1, self.bias.shape[0], 1, 1)In the code snippet below you can find the class PixelNorm to normalize Z before the Noise Mapping Network.
class PixelNorm(nn.Module):
def __init__(self):
super(PixelNorm, self).__init__()
self.epsilon = 1e-8
def forward(self, x):
return x / torch.sqrt(torch.mean(x ** 2, dim=1, keepdim=True) + self.epsilon) In the code snippet below you can find the class ConvBock that will help us create the discriminator.
class ConvBlock(nn.Module):
def __init__(self, in_channels, out_channels):
super(ConvBlock, self).__init__()
self.conv1 = WSConv2d(in_channels, out_channels)
self.conv2 = WSConv2d(out_channels, out_channels)
self.leaky = nn.LeakyReLU(0.2)
def forward(self, x):
x = self.leaky(self.conv1(x))
x = self.leaky(self.conv2(x))
return xIn the code snippet below you can find the class Discriminatowich is the same as in ProGAN.
class Discriminator(nn.Module):
def __init__(self, in_channels, img_channels=3):
super(Discriminator, self).__init__()
self.prog_blocks, self.rgb_layers = nn.ModuleList([]), nn.ModuleList([])
self.leaky = nn.LeakyReLU(0.2)
# here we work back ways from factors because the discriminator
# should be mirrored from the generator. So the first prog_block and
# rgb layer we append will work for input size 1024x1024, then 512->256-> etc
for i in range(len(factors) - 1, 0, -1):
conv_in = int(in_channels * factors[i])
conv_out = int(in_channels * factors[i - 1])
self.prog_blocks.append(ConvBlock(conv_in, conv_out))
self.rgb_layers.append(
WSConv2d(img_channels, conv_in, kernel_size=1, stride=1, padding=0)
)
# perhaps confusing name "initial_rgb" this is just the RGB layer for 4x4 input size
# did this to "mirror" the generator initial_rgb
self.initial_rgb = WSConv2d(
img_channels, in_channels, kernel_size=1, stride=1, padding=0
)
self.rgb_layers.append(self.initial_rgb)
self.avg_pool = nn.AvgPool2d(
kernel_size=2, stride=2
) # down sampling using avg pool
# this is the block for 4x4 input size
self.final_block = nn.Sequential(
# +1 to in_channels because we concatenate from MiniBatch std
WSConv2d(in_channels + 1, in_channels, kernel_size=3, padding=1),
nn.LeakyReLU(0.2),
WSConv2d(in_channels, in_channels, kernel_size=4, padding=0, stride=1),
nn.LeakyReLU(0.2),
WSConv2d(
in_channels, 1, kernel_size=1, padding=0, stride=1
), # we use this instead of linear layer
)
def fade_in(self, alpha, downscaled, out):
"""Used to fade in downscaled using avg pooling and output from CNN"""
# alpha should be scalar within [0, 1], and upscale.shape == generated.shape
return alpha * out + (1 - alpha) * downscaled
def minibatch_std(self, x):
batch_statistics = (
torch.std(x, dim=0).mean().repeat(x.shape[0], 1, x.shape[2], x.shape[3])
)
# we take the std for each example (across all channels, and pixels) then we repeat it
# for a single channel and concatenate it with the image. In this way the discriminator
# will get information about the variation in the batch/image
return torch.cat([x, batch_statistics], dim=1)
def forward(self, x, alpha, steps):
# where we should start in the list of prog_blocks, maybe a bit confusing but
# the last is for the 4x4. So example let's say steps=1, then we should start
# at the second to last because input_size will be 8x8. If steps==0 we just
# use the final block
cur_step = len(self.prog_blocks) - steps
# convert from rgb as initial step, this will depend on
# the image size (each will have it's on rgb layer)
out = self.leaky(self.rgb_layers[cur_step](x))
if steps == 0: # i.e, image is 4x4
out = self.minibatch_std(out)
return self.final_block(out).view(out.shape[0], -1)
# because prog_blocks might change the channels, for down scale we use rgb_layer
# from previous/smaller size which in our case correlates to +1 in the indexing
downscaled = self.leaky(self.rgb_layers[cur_step + 1](self.avg_pool(x)))
out = self.avg_pool(self.prog_blocks[cur_step](out))
# the fade_in is done first between the downscaled and the input
# this is opposite from the generator
out = self.fade_in(alpha, downscaled, out)
for step in range(cur_step + 1, len(self.prog_blocks)):
out = self.prog_blocks[step](out)
out = self.avg_pool(out)
out = self.minibatch_std(out)
return self.final_block(out).view(out.shape[0], -1)Generator
In the generator architecture, we have some patterns that repeat so let's first create a class for it to make our code as clean as possible, let's name the class GenBlock which will be inherited from nn.Module.
- In the init part we send in_channels, out_channels, and w_dim, then we initialize conv1 by WSConv2d which maps in_channels to out_channels, conv2 by WSConv2d which maps out_channels to out_channels, leaky by Leaky ReLU with a slope of 0.2 as they use in the paper, inject_noise1, inject_noise2 by the InjectNoise, adain1, and adain2 by AdaIN
- In the forward part, we send x, and we pass it to conv1 then to inject_noise1 with leaky, then we normalize it with adain1, and again we pass that into conv2 then to inject_noise2 with leaky and we normalize it with adain2. And finally, we return x.
class GenBlock(nn.Module):
def __init__(self, in_channels, out_channels, w_dim):
super(GenBlock, self).__init__()
self.conv1 = WSConv2d(in_channels, out_channels)
self.conv2 = WSConv2d(out_channels, out_channels)
self.leaky = nn.LeakyReLU(0.2, inplace=True)
self.inject_noise1 = InjectNoise(out_channels)
self.inject_noise2 = InjectNoise(out_channels)
self.adain1 = AdaIN(out_channels, w_dim)
self.adain2 = AdaIN(out_channels, w_dim)
def forward(self, x, w):
x = self.adain1(self.leaky(self.inject_noise1(self.conv1(x))), w)
x = self.adain2(self.leaky(self.inject_noise2(self.conv2(x))), w)
return xNow we have all that we need to create the generator.
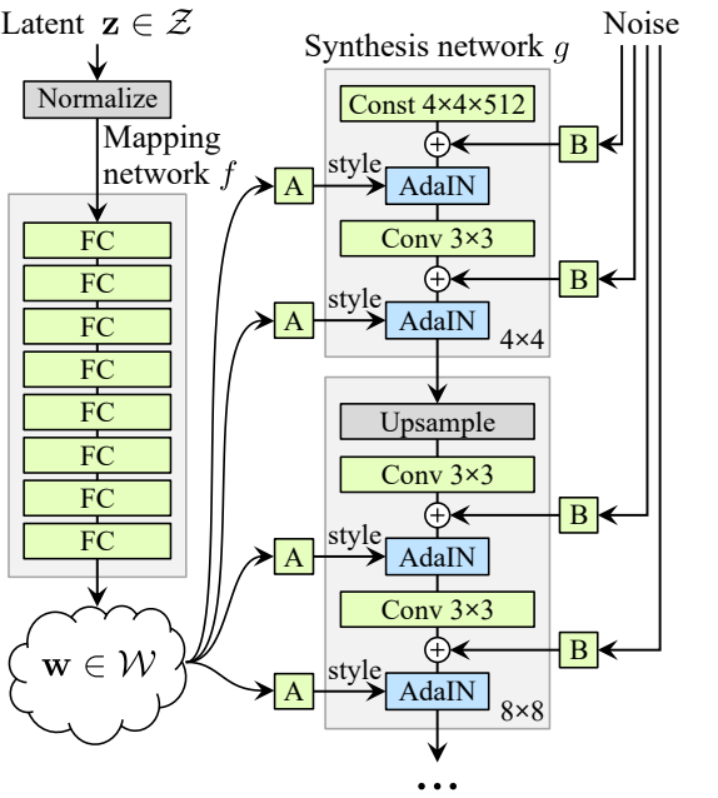
- in the init part let's initialize 'starting_constant' by constant 4 x 4 (x 512 channel for the original paper, and 256 in our case) tensor which is put through an iteration of the generator, map by 'MappingNetwork', initial_adain1, initial_adain2 by AdaIN, initial_noise1, initial_noise2 by InjectNoise, initial_conv by a conv layer that map in_channels to itself, leaky by Leaky ReLU with a slope of 0.2, initial_rgb by WSConv2d that maps in_channels to img_channels wi=hich is 3 for RGB, prog_blocks by ModuleList() that will contain all the progressive blocks (we indicate convolution input/output channels by multiplicate in_channels which is 512 in paper and 256 in our case with factors), and rgb_blocks by ModuleList() that will contain all the RGB blocks.
- To fade in new layers (an origin component of ProGAN), we add the fade_in part, which we send alpha, scaled, and generated, and we return [tanh(alpha∗generated+(1−alpha)∗upscale)], The reason why we use tanh is that will be the output(the generated image) and we want the pixels to be range between 1 and -1.
- In the forward part, we send the noise (Z_dim), the alpha value which is going to fade in slowly during training (alpha is between 0 and 1), and steps which is the number of the current resolution that we are working with, we pass x into the map to get the intermediate noise vector W, we pass starting_constant to initial_noise1, apply for it and for W initial_adain1, then we passe it into initial_conv, and again we add initial_noise2 for it with leaky as activation function, and apply for it and W initial_adain2. Then we check if steps = 0 if it is, then all we want to do is run it through the initial RGB and we have done, otherwise, we loop over the number of steps, and in each loop we upscaling(upscaled) and we run through the progressive block that corresponds to that resolution(out). In the end, we return fade_in that takes alpha, final_out, and final_upscaled after mapping it to RGB.
class Generator(nn.Module):
def __init__(self, z_dim, w_dim, in_channels, img_channels=3):
super(Generator, self).__init__()
self.starting_constant = nn.Parameter(torch.ones((1, in_channels, 4, 4)))
self.map = MappingNetwork(z_dim, w_dim)
self.initial_adain1 = AdaIN(in_channels, w_dim)
self.initial_adain2 = AdaIN(in_channels, w_dim)
self.initial_noise1 = InjectNoise(in_channels)
self.initial_noise2 = InjectNoise(in_channels)
self.initial_conv = nn.Conv2d(in_channels, in_channels, kernel_size=3, stride=1, padding=1)
self.leaky = nn.LeakyReLU(0.2, inplace=True)
self.initial_rgb = WSConv2d(
in_channels, img_channels, kernel_size=1, stride=1, padding=0
)
self.prog_blocks, self.rgb_layers = (
nn.ModuleList([]),
nn.ModuleList([self.initial_rgb]),
)
for i in range(len(factors) - 1): # -1 to prevent index error because of factors[i+1]
conv_in_c = int(in_channels * factors[i])
conv_out_c = int(in_channels * factors[i + 1])
self.prog_blocks.append(GenBlock(conv_in_c, conv_out_c, w_dim))
self.rgb_layers.append(
WSConv2d(conv_out_c, img_channels, kernel_size=1, stride=1, padding=0)
)
def fade_in(self, alpha, upscaled, generated):
# alpha should be scalar within [0, 1], and upscale.shape == generated.shape
return torch.tanh(alpha * generated + (1 - alpha) * upscaled)
def forward(self, noise, alpha, steps):
w = self.map(noise)
x = self.initial_adain1(self.initial_noise1(self.starting_constant), w)
x = self.initial_conv(x)
out = self.initial_adain2(self.leaky(self.initial_noise2(x)), w)
if steps == 0:
return self.initial_rgb(x)
for step in range(steps):
upscaled = F.interpolate(out, scale_factor=2, mode="bilinear")
out = self.prog_blocks[step](upscaled, w)
# The number of channels in upscale will stay the same, while
# out which has moved through prog_blocks might change. To ensure
# we can convert both to rgb we use different rgb_layers
# (steps-1) and steps for upscaled, out respectively
final_upscaled = self.rgb_layers[steps - 1](upscaled)
final_out = self.rgb_layers[steps](out)
return self.fade_in(alpha, final_upscaled, final_out)
Utils
In the code snippet below you can find the generate_examples function that takes the generator gen, the number of steps to identify the current resolution, and a number n=100. The goal of this function is to generate n fake images and save them as a result.
def generate_examples(gen, steps, n=100):
gen.eval()
alpha = 1.0
for i in range(n):
with torch.no_grad():
noise = torch.randn(1, Z_DIM).to(DEVICE)
img = gen(noise, alpha, steps)
if not os.path.exists(f'saved_examples/step{steps}'):
os.makedirs(f'saved_examples/step{steps}')
save_image(img*0.5+0.5, f"saved_examples/step{steps}/img_{i}.png")
gen.train()In the code snippet below you can find the gradient_penalty function for WGAN-GP loss.
def gradient_penalty(critic, real, fake, alpha, train_step, device="cpu"):
BATCH_SIZE, C, H, W = real.shape
beta = torch.rand((BATCH_SIZE, 1, 1, 1)).repeat(1, C, H, W).to(device)
interpolated_images = real * beta + fake.detach() * (1 - beta)
interpolated_images.requires_grad_(True)
# Calculate critic scores
mixed_scores = critic(interpolated_images, alpha, train_step)
# Take the gradient of the scores with respect to the images
gradient = torch.autograd.grad(
inputs=interpolated_images,
outputs=mixed_scores,
grad_outputs=torch.ones_like(mixed_scores),
create_graph=True,
retain_graph=True,
)[0]
gradient = gradient.view(gradient.shape[0], -1)
gradient_norm = gradient.norm(2, dim=1)
gradient_penalty = torch.mean((gradient_norm - 1) ** 2)
return gradient_penaltyTraining
In this section, we will train our StyleGAN
Bring this project to life
Train function
For the train function, we send critic (which is the discriminator), gen(generator), loader, dataset, step, alpha, and optimizer for the generator and for the critic.
We start by looping over all the mini-batch sizes that we create with the DataLoader, and we take just the images because we don't need a label.
Then we set up the training for the discriminator\Critic when we want to maximize E(critic(real)) - E(critic(fake)). This equation means how much the critic can distinguish between real and fake images.
After that, we set up the training for the generator when we want to maximize E(critic(fake)).
Finally, we update the loop and the alpha value for fade_in and ensure that it is between 0 and 1, and we return it.
def train_fn(
critic,
gen,
loader,
dataset,
step,
alpha,
opt_critic,
opt_gen,
):
loop = tqdm(loader, leave=True)
for batch_idx, (real, _) in enumerate(loop):
real = real.to(DEVICE)
cur_batch_size = real.shape[0]
noise = torch.randn(cur_batch_size, Z_DIM).to(DEVICE)
fake = gen(noise, alpha, step)
critic_real = critic(real, alpha, step)
critic_fake = critic(fake.detach(), alpha, step)
gp = gradient_penalty(critic, real, fake, alpha, step, device=DEVICE)
loss_critic = (
-(torch.mean(critic_real) - torch.mean(critic_fake))
+ LAMBDA_GP * gp
+ (0.001 * torch.mean(critic_real ** 2))
)
critic.zero_grad()
loss_critic.backward()
opt_critic.step()
gen_fake = critic(fake, alpha, step)
loss_gen = -torch.mean(gen_fake)
gen.zero_grad()
loss_gen.backward()
opt_gen.step()
# Update alpha and ensure less than 1
alpha += cur_batch_size / (
(PROGRESSIVE_EPOCHS[step] * 0.5) * len(dataset)
)
alpha = min(alpha, 1)
loop.set_postfix(
gp=gp.item(),
loss_critic=loss_critic.item(),
)
return alpha
Training
Now since we have everything let's put them together to train our StyleGAN.
We start by initializing the generator, the discriminator/critic, and optimizers, then convert the generator and the critic into train mode, then loop over PROGRESSIVE_EPOCHS, and in each loop, we call the train function number of epoch times, then we generate some fake images and save them, as a result, using generate_examples function, and finally, we progress to the next image resolution.
gen = Generator(
Z_DIM, W_DIM, IN_CHANNELS, img_channels=CHANNELS_IMG
).to(DEVICE)
critic = Discriminator(IN_CHANNELS, img_channels=CHANNELS_IMG).to(DEVICE)
# initialize optimizers
opt_gen = optim.Adam([{"params": [param for name, param in gen.named_parameters() if "map" not in name]},
{"params": gen.map.parameters(), "lr": 1e-5}], lr=LEARNING_RATE, betas=(0.0, 0.99))
opt_critic = optim.Adam(
critic.parameters(), lr=LEARNING_RATE, betas=(0.0, 0.99)
)
gen.train()
critic.train()
# start at step that corresponds to img size that we set in config
step = int(log2(START_TRAIN_AT_IMG_SIZE / 4))
for num_epochs in PROGRESSIVE_EPOCHS[step:]:
alpha = 1e-5 # start with very low alpha
loader, dataset = get_loader(4 * 2 ** step)
print(f"Current image size: {4 * 2 ** step}")
for epoch in range(num_epochs):
print(f"Epoch [{epoch+1}/{num_epochs}]")
alpha = train_fn(
critic,
gen,
loader,
dataset,
step,
alpha,
opt_critic,
opt_gen
)
generate_examples(gen, step)
step += 1 # progress to the next img size
Result
Hopefully, you will be able to follow all of the steps and get a good understanding of how to implement StyleGAN in the right way. Now let's check out the results that we obtain after training this model in this dataset with 128*x 128 resolution.

Conclusion
In this article, we make a clean, simple, and readable implementation from scratch of StyleGAN1 using PyTorch. we replicate the original paper as closely as possible, so if you read the paper the implementation should be pretty much identical.
In the upcoming articles, we will explain in depth and implement from scratch StyleGAN2 which is an improvement over StyleGAN1.










