An Overview of Epistemic Uncertainty in Deep Learning

There is a general understanding that when out-of-sample images are fed to a deep learning classifier, the model still attempts to classify the image as a member of one of the classes present in it's training set; at this point aleatoric/data uncertainty sets in.

Now consider a scenario where edge cases of images present in the training dataset are fed to the model. In this case, the model attempts to classify the image as usual but it definitely will be less certain. How do we perceive this sort of uncertainty? In this article we will be attempting to do just that in the context of image classifiers.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
import torchvision.datasets as Datasets
from torch.utils.data import Dataset, DataLoader
import numpy as np
import matplotlib.pyplot as plt
import cv2
from tqdm.notebook import tqdm
import seaborn as sns
from torchvision.utils import make_grid

if torch.cuda.is_available():
  device = torch.device('cuda:0')
  print('Running on the GPU')
else:
  device = torch.device('cpu')
  print('Running on the CPU')

Epistemic/Model Uncertainty

Epistemic uncertainty occurs when a deep learning model encounters an instance of data which it should ordinarily be able to classify but it can't possibly be quite certain due to an insufficiency of similar images in the training dataset.

In simpler terms, consider a model built to classify cars. The training dataset is filled with cars of different classes from a variety of angles, let's assume that the model is then supplied an image of a car flipped on it's side at inference time; yes the model is built to classify cars and yes, the model will provide a classification for that particular flipped car, but the model had not come across a flipped car at training time so how reliable will that particular classification actually be?

An Unsure Model

When it comes to classifiers their outputs are not exactly a measure of certainty of a data instance belonging to a particular class, they are more of a measure of similarity or closeness to a particular class. For instance, if a cat and dog classifier is feed an image of a horse and the model predicts that image to be 70% cat, the model simply implies that the horse looks more catlike than doglike. That particular classification is based on the parameters of the model as optimized for that specific architecture.

Armed with this knowledge we can begin to realize that perhaps if another cat-dog classifier were to be trained, attaining similar accuracy as the first model, it might think the horse image is more doglike than catlike. The same thing applies to edge images, when different models of different architectures trained for the exact same task encounter these images there is a tendency to classify them differently as they are all unsure of what that particular instance of data really is.

Bayesian Models

As stated in the previous section, if we train a number of different models, say 50 for instance, all for the same task and then feed the same image through them we can infer that if an overwhelming majority of models classify said image to belong to a specific class then the models are certain about that particular image.

However,  if there is a considerable difference in classification across models then we can begin to look at said image as one which the models are not certain about. When this is done, it can be said that we are making a Bayesian inference on that particular image.

Bayesian Neural Networks

We can all agree that training 50 different deep learning models is a daunting task as it is would be both computation and time expensive. However, there is a way to mimic the essence of multiple models present in a single model; and that's by utilizing an approach called Monte Carlo Dropout.

Dropout is typically used in neural networks for regularization. It's working principle is hinged in the switching off of random neurons for every pass through the neural network so as to create a slightly deferent architecture and prevent overfitting. Dropout is turned on during training but turned off at inference/evaluation.

If it is left turned on during inference then we can simulate the presence of different architectures each time we utilize the model. This is essentially what Monte Carlo Dropout entails and any neural network used in this way is termed a Bayesian Neural Network.

Replicating a Bayesian Neural Network

For the sake of this article, we will be incorporating dropout layers into the Lenet-5 architecture in a bid to create a Bayesian neural network whist utilizing the MNIST dataset for training and validation.

Dataset

The dataset to be utilized for this task is the MNIST dataset. and it can be loaded in PyTorch using the code cell below.

#  loading training data
training_set = Datasets.MNIST(root='./', download=True,
                              transform=transforms.Compose([transforms.ToTensor(),
                                                            transforms.Resize((32, 32)),
                                                            transforms.Normalize(0.137, 0.3081)]))

#  loading validation data
validation_set = Datasets.MNIST(root='./', download=True, train=False,
                                transform=transforms.Compose([transforms.ToTensor(),
                                                              transforms.Resize((32, 32)),
                                                              transforms.Normalize(0.137, 0.3081)]))

Model Architecture

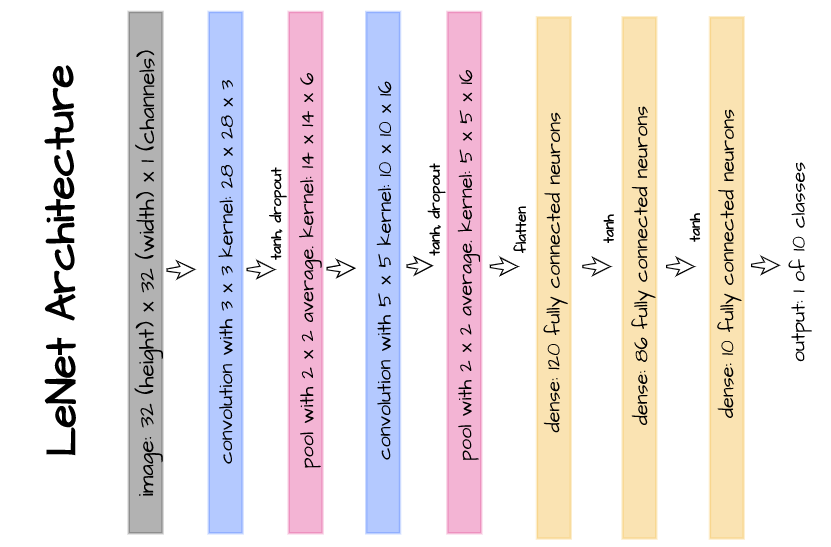
The above illustrated architecture entails the use of dropout layers after the first and second convolution layers in the lenet-5 architecture. It is replicated in the code cell below using PyTorch.

class LeNet5_Dropout(nn.Module):
  def __init__(self):
    super().__init__()
    self.conv1 = nn.Conv2d(1, 6, 5)
    self.dropout = nn.Dropout2d()
    self.pool1 = nn.AvgPool2d(2)
    self.conv2 = nn.Conv2d(6, 16, 5)
    self.pool2 = nn.AvgPool2d(2)
    self.linear1 = nn.Linear(5*5*16, 120)
    self.linear2 = nn.Linear(120, 84)
    self.linear3 = nn. Linear(84, 10)

  def forward(self, x):
    x = x.view(-1, 1, 32, 32)

    #----------
    # LAYER 1
    #----------
    output_1 = self.conv1(x)
    output_1 = torch.tanh(output_1)
    output_1 = self.dropout(output_1)
    output_1 = self.pool1(output_1)
    
    #----------
    # LAYER 2
    #----------
    output_2 = self.conv2(output_1)
    output_2 = torch.tanh(output_2)
    output_2 = self.dropout(output_2)
    output_2 = self.pool2(output_2)
    
    #----------
    # FLATTEN
    #----------
    output_2 = output_2.view(-1, 5*5*16)

    #----------
    # LAYER 3
    #----------
    output_3 = self.linear1(output_2)
    output_3 = torch.tanh(output_3)
    
    #----------
    # LAYER 4
    #----------
    output_4 = self.linear2(output_3)
    output_4 = torch.tanh(output_4)
    
    #-------------
    # OUTPUT LAYER
    #-------------
    output_5 = self.linear3(output_4)
    return(F.softmax(output_5, dim=1))

Model Training, Validation and Inference

Below, a class is defined which encapsulates model training, validation and inference. For the inference method 'predict()', evaluation mode can be switched off when Bayesian inference is being sought, keeping dropout in place thereby allowing the model to be used for both regular and Bayesian inference as desired.

class ConvolutionalNeuralNet():
  def __init__(self, network):
    self.network = network.to(device)
    self.optimizer = torch.optim.Adam(self.network.parameters(), lr=1e-3)

  def train(self, loss_function, epochs, batch_size, 
            training_set, validation_set):
    
    #  creating log
    log_dict = {
        'training_loss_per_batch': [],
        'validation_loss_per_batch': [],
        'training_accuracy_per_epoch': [],
        'training_recall_per_epoch': [],
        'training_precision_per_epoch': [],
        'validation_accuracy_per_epoch': [],
        'validation_recall_per_epoch': [],
        'validation_precision_per_epoch': []
    } 

    #  defining weight initialization function
    def init_weights(module):
      if isinstance(module, nn.Conv2d):
        torch.nn.init.xavier_uniform_(module.weight)
        module.bias.data.fill_(0.01)
      elif isinstance(module, nn.Linear):
        torch.nn.init.xavier_uniform_(module.weight)
        module.bias.data.fill_(0.01)

    #  defining accuracy function
    def accuracy(network, dataloader):
      network.eval()
      
      all_predictions = []
      all_labels = []

      #  computing accuracy
      total_correct = 0
      total_instances = 0
      for images, labels in tqdm(dataloader):
        images, labels = images.to(device), labels.to(device)
        all_labels.extend(labels)
        predictions = torch.argmax(network(images), dim=1)
        all_predictions.extend(predictions)
        correct_predictions = sum(predictions==labels).item()
        total_correct+=correct_predictions
        total_instances+=len(images)
      accuracy = round(total_correct/total_instances, 3)

      #  computing recall and precision
      true_positives = 0
      false_negatives = 0
      false_positives = 0
      for idx in range(len(all_predictions)):
        if all_predictions[idx].item()==1 and  all_labels[idx].item()==1:
          true_positives+=1
        elif all_predictions[idx].item()==0 and all_labels[idx].item()==1:
          false_negatives+=1
        elif all_predictions[idx].item()==1 and all_labels[idx].item()==0:
          false_positives+=1
      try:
        recall = round(true_positives/(true_positives + false_negatives), 3)
      except ZeroDivisionError:
        recall = 0.0
      try:
        precision = round(true_positives/(true_positives + false_positives), 3)
      except ZeroDivisionError:
        precision = 0.0
      return accuracy, recall, precision

    #  initializing network weights
    self.network.apply(init_weights)

    #  creating dataloaders
    train_loader = DataLoader(training_set, batch_size)
    val_loader = DataLoader(validation_set, batch_size)

    
    for epoch in range(epochs):
      print(f'Epoch {epoch+1}/{epochs}')
      train_losses = []

      #  training
      #  setting convnet to training mode
      self.network.train()
      print('training...')
      for images, labels in tqdm(train_loader):
        #  sending data to device
        images, labels = images.to(device), labels.to(device)
        #  resetting gradients
        self.optimizer.zero_grad()
        #  making predictions
        predictions = self.network(images)
        #  computing loss
        loss = loss_function(predictions, labels)
        log_dict['training_loss_per_batch'].append(loss.item())
        train_losses.append(loss.item())
        #  computing gradients
        loss.backward()
        #  updating weights
        self.optimizer.step()
      with torch.no_grad():
        print('deriving training accuracy...')
        #  computing training accuracy
        train_accuracy, train_recall, train_precision = accuracy(self.network, train_loader)
        log_dict['training_accuracy_per_epoch'].append(train_accuracy)
        log_dict['training_recall_per_epoch'].append(train_recall)
        log_dict['training_precision_per_epoch'].append(train_precision)

      #  validation
      print('validating...')
      val_losses = []

      #  setting convnet to evaluation mode
      self.network.eval()

      with torch.no_grad():
        for images, labels in tqdm(val_loader):
          #  sending data to device
          images, labels = images.to(device), labels.to(device)
          #  making predictions
          predictions = self.network(images)
          #  computing loss
          val_loss = loss_function(predictions, labels)
          log_dict['validation_loss_per_batch'].append(val_loss.item())
          val_losses.append(val_loss.item())
        #  computing accuracy
        print('deriving validation accuracy...')
        val_accuracy, val_recall, val_precision = accuracy(self.network, val_loader)
        log_dict['validation_accuracy_per_epoch'].append(val_accuracy)
        log_dict['validation_recall_per_epoch'].append(val_recall)
        log_dict['validation_precision_per_epoch'].append(val_precision)

      train_losses = np.array(train_losses).mean()
      val_losses = np.array(val_losses).mean()

      print(f'training_loss: {round(train_losses, 4)}  training_accuracy: '+
      f'{train_accuracy}  training_recall: {train_recall}  training_precision: {train_precision} *~* validation_loss: {round(val_losses, 4)} '+  
      f'validation_accuracy: {val_accuracy}  validation_recall: {val_recall}  validation_precision: {val_precision}\n')
      
    return log_dict

  def predict(self, x, eval=True):
    if eval:
      with torch.no_grad():
        return self.network(x)
    else:
      with torch.no_grad():
        self.network.train()
        return self.network(x)

Model Training

The Lenet-5 architecture is defined as a member of the 'ConvolutionalNeuralNet()' class and is trained for 10 epochs with parameters as defined in the code cell below.

model = ConvolutionalNeuralNet(LeNet5_Dropout())

#  training model and deriving metrics
log_dict = model.train(nn.CrossEntropyLoss(), epochs=10, batch_size=64, 
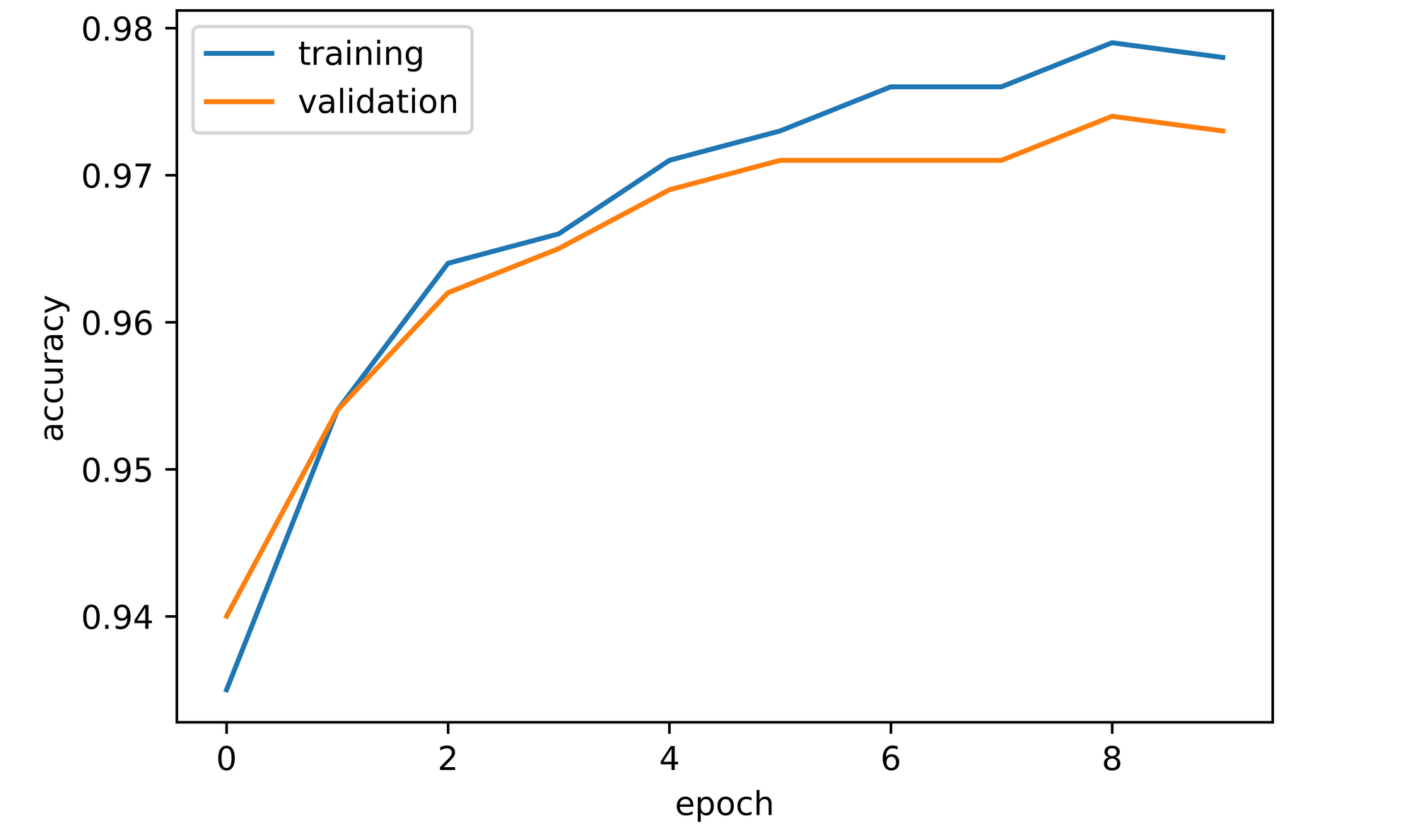
                           training_set=training_set, validation_set=validation_set)

From the accuracy plots, it can be seen that both training and validation accuracy increase over the course of model training. Training accuracy peaked at a value of just under 98% by the 10th epoch, while validation accuracy attained a value of approximately 97.3% at the same point.

Bayesian Inference

With the model trained, it is now time to make some Bayesian inference in a bid to see how confident our model is about it's classifications. From exploring the dataset, I have identified two images from the dataset with one being a typical figure 8 and another being a weird looking figure 8 which I have deemed to be an edge case in the class of 8s.

These images can be found at index 61 and 591 respectively. For the sake of suspense I will not be revealing which is which for now.

#  extracting two images from the validation set
image_1 = validation_set[61]
image_2 = validation_set[591]

The below defined function takes in a model, an image and a desired number of models for Bayesian inference as parameters. The function then returns a count plot of the classification made by all the models as evaluation is turned off and dropout is kept in place.

def epistemic_check(model, image, model_number=20):
  """
  This model returns a count plot of model classifications
  """
  confidence = []

  for i in range(model_number):
    confidence.append(torch.argmax(F.softmax(model.predict(image.to(device), 
                                                           eval=False), dim=1)).item())

  return sns.countplot(x=confidence)

Image 1

Utilizing the function and setting number of models to 100, we perform inference on image_1. From the plot returned it is seen that of all 100 models used to classify the image, only a hand-full of them mistook the image as a figure 2 with over 90% of them classifying the image as a figure 8. A pointer to the fact that the model is quite certain about this image.

epistemic_check(model, image_1[0], 100)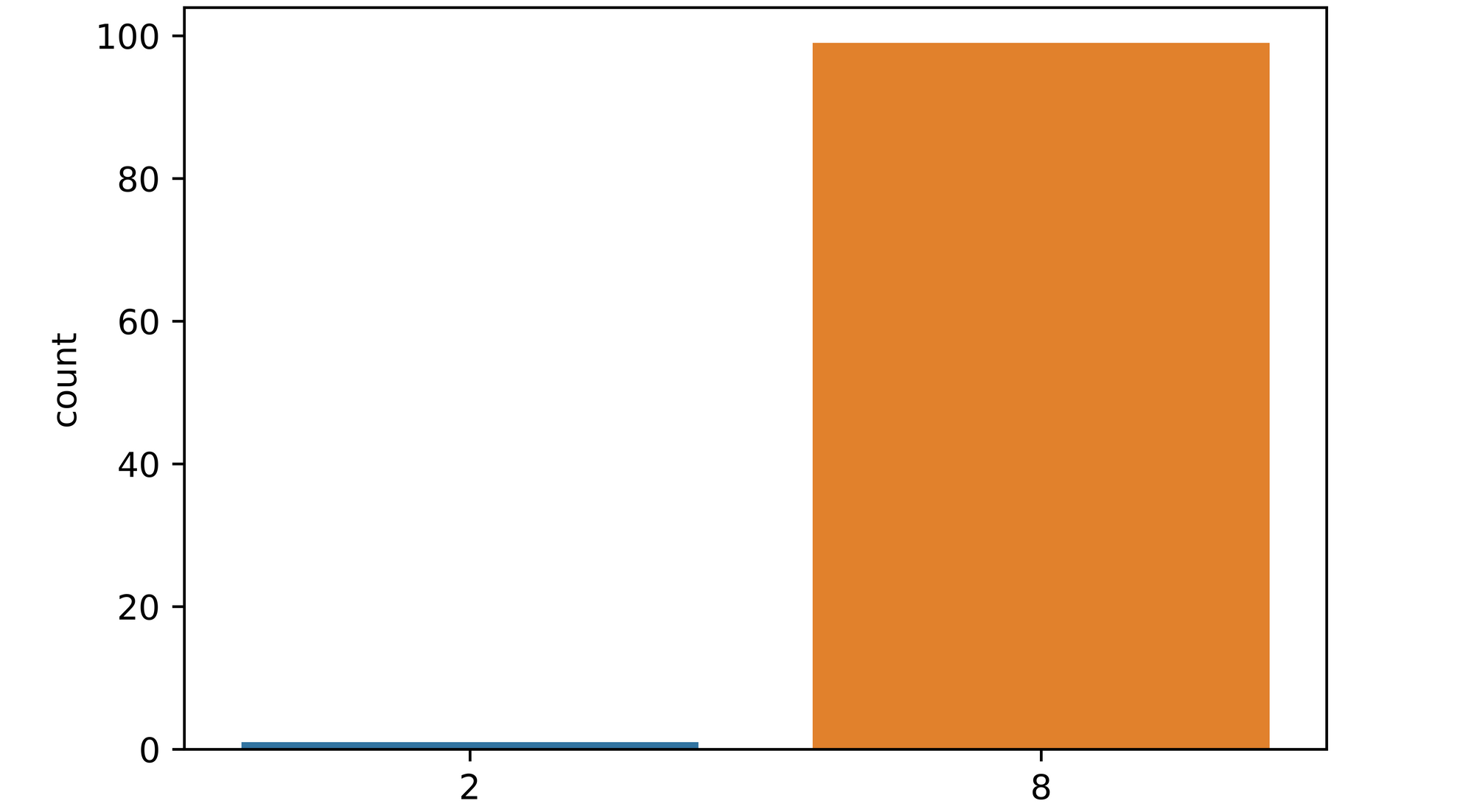

Visualizing the image, we can see that it looks like a typical figure 8 and as such should be easily classifiable by the model.

Image 2

Passing image_2 to the function and keeping all other parameters the same yields some rather interesting results. From the plot returned, it can be seen that a significant proportion of the 100 models (over 40) mistook the image to be that of a figure 3, while about 4 models mistook the image as either a 7 or a 9. Unlike the first image, the models are essentially in disagreement over what the image actually is, a pointer to epistemic uncertainty.

epistemic_check(model, image_2[0], 100)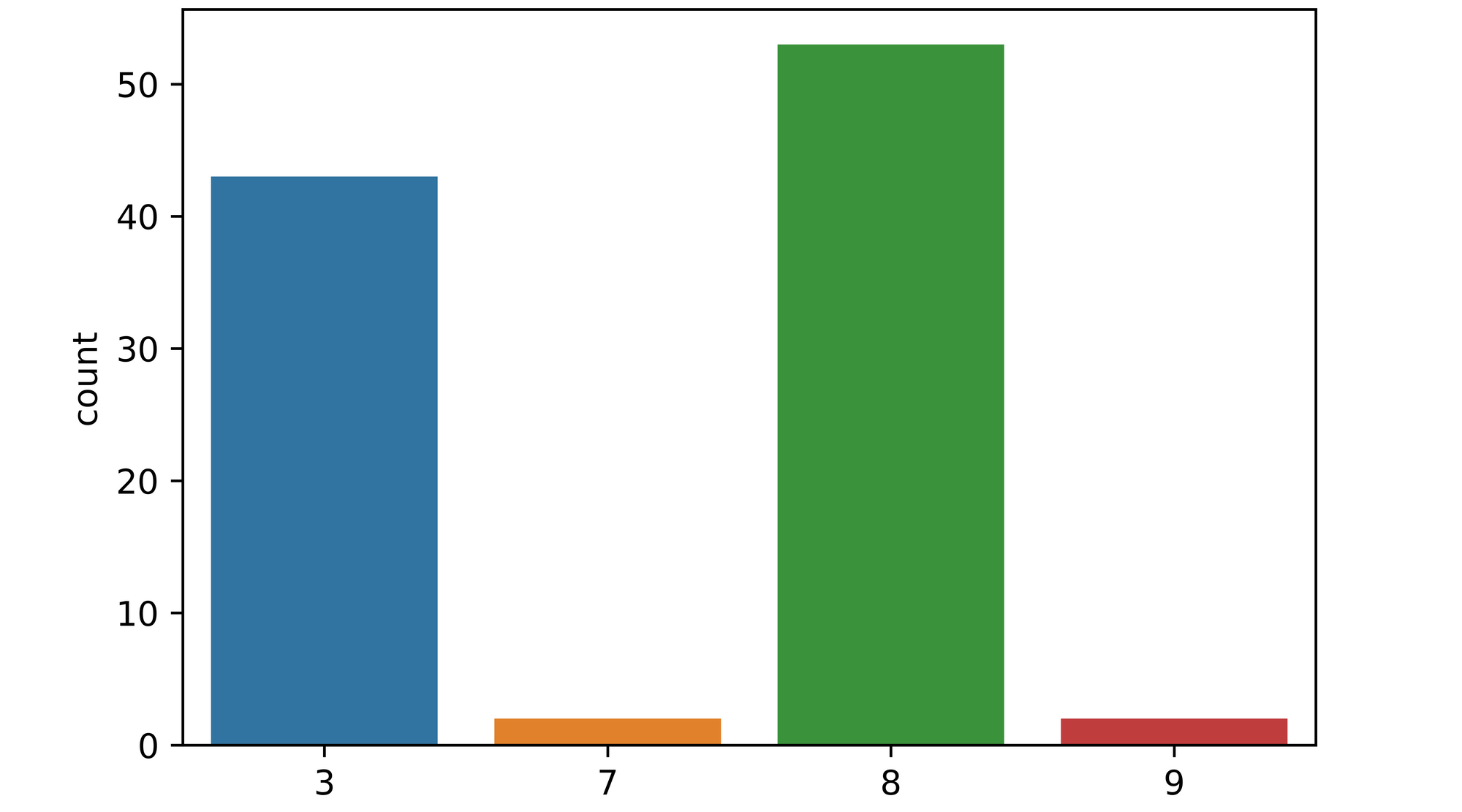

Looking at the image, it can be seem that it is quite peculiar one as it does in-fact resemble a figure 3 in some lights even though it has been labeled as a figure 8 in the dataset.

Final Remarks

In this article, we explored a broad overview of epistemic uncertainty in deep learning classifiers. Although we did not explore how to quantify this sort of uncertainty, we were able to develop an intuition about how an ensemble of models can be used to detect its presence for a particular image instance.