Measuring Text Similarity Using the Levenshtein Distance

In word processing or text chat applications, it's common that users make some unintended spelling mistakes. It could be as simple as writing "helo" (single "l") rather than "hello". Luckily, nowadays such applications can detect that there is a spelling mistake because the word "helo" does not exist in the English language dictionary. The misspelled word is highlighted, for example, by a red underline.

Thanks to advancements in artificial intelligence (AI), such applications are more than just detecting a spelling mistake; they can now also make suggestions to fix it, or do so automatically. Moreover, applications are intelligent enough to suggest autocompleting words based on only some of the first characters. How are such suggestions made? We'll see how in this tutorial.

This tutorial discusses the Levenshtein distance, which calculates the distance between two words and returns a number representing how similar they are. The lower the distance (i.e. the smaller the number returned), the more similar they are. So by comparing the word "helo" with the words in the dictionary, we can find the closest match, "hello", which will be a suggested fix.

The tutorial works through a step-by-step dynamic programming example that clarifies how the Levenshtein distance is calculated. The distance is then implemented in Python.

The sections covered in this tutorial are as follows:

• How Does the Levenshtein Distance Work?
• Step-by-Step Calculation of the Levenshtein Distance Using Dynamic Programming
• Levenshtein Distance Implementation in Python

How Does the Levenshtein Distance Work?

The Levenshtein distance is a similarity measure between words. Given two words, the distance measures the number of edits needed to transform one word into another. There are three techniques that can be used for editing:

1. Insertion
2. Deletion
3. Replacement (substitution)

Each of these three operations adds 1 to the distance. Let's make things simpler.

A General Example

Given two words, hello and hello, the Levenshtein distance is zero because the words are identical.

For the two words helo and hello, it is obvious that there is a missing character "l". Thus to transform the word helo to hello all we need to do is insert that character. The distance, in this case, is 1 because there is only one edit needed.

On the other hand, for the two words kelo and hello more than just inserting the character "l" is needed. We also need to substitute the character "k" with "h". After such edits, the word kelo is converted into hello. The distance is therefore 2, because there are two operations applied: substitution and insertion.

For the two words kel and hello, we must first replace "k" with "h", then add a missing "l" followed by an "o" at the end. As a result, the distance is 3 because there are three operations applied.

Note that the previous discussion is not strategic. We're following predefined steps that could be applied to any two words to transform one word into another. The strategy that we are going to discuss now is how to calculate a distance matrix using dynamic programming. Given two words A and B, the distance matrix holds the distances between all prefixes of the word A and all prefixes of the word B.

A Strategic Example

For the word kelo, the possible prefixes are k, ke, kel, and kelo for a total of four prefixes. For the word hello, the prefixes are h, he, hel, hell, and hello for a total of five prefixes. The distance matrix calculates the distance between all prefixes in the two words. This creates a matrix with 4 rows and 5 columns (or 5 rows and 4 columns, depending on your choice of which word represents the rows and which represents the columns–see the image below).

Starting with the first prefix in the word kelo which is k, we'll compare it to all five prefixes in the word hello. The first one will be h. What is the Levenshtein distance between k and h? Because all we need to do is substitute the character k by h, the distance is 1. Let's move to the next prefix in the word hello which is he.

What is the Levenshtein distance between k and he? Because the prefix k contains a single character and he contains more than one character, we can be 100% sure that a new character will need to be inserted. To transform k to he, first the character k is replaced by h, and then we add e. To transform k to he, the distance is therefore 2.

Now for the third prefix. What is the distance between k and hel? We'll do the same as above, but we'll need to add another character, l, as well. The final distance is therefore 3.

The process continues until we've calculated the distance between the first prefix in the word kelo, or k, and all of the 5 prefixes in the second word hello. The distances are simply 1, 2, 3, 4, and 5; they simply increase by 1 (which makes sense, since we must add one more character for each subsequent prefix).

Note that the first distance is 1 just because the first two characters in the first two prefixes ("k" and "h") do not match. If the two words were helo and hello, then the first 2 prefixes (h and h) match and thus the first distance will be 0. Thus, the distances between the first prefix of helo (h) and the 5 prefixes in hello will be 0, 1, 2, 3, and 4.

After calculating the distances between the first prefix of the first word and all prefixes of the second word, the process continues to calculate the distances between the remaining prefixes of the first word and the prefixes of the second word.

The next section discusses how the distance matrix is calculated using the dynamic programming approach.

Preparing the Distance Matrix

In this section we are going to prepare the distance matrix that will be used to calculate the distance between the 2 words kelm and hello using the dynamic programming approach. The next section will go through the steps of filling such a matrix.

It is important to know that dynamic programming solves a complex problem by breaking it down into a number of simple problems. By solving such simple problems, the complex problem will be solved.

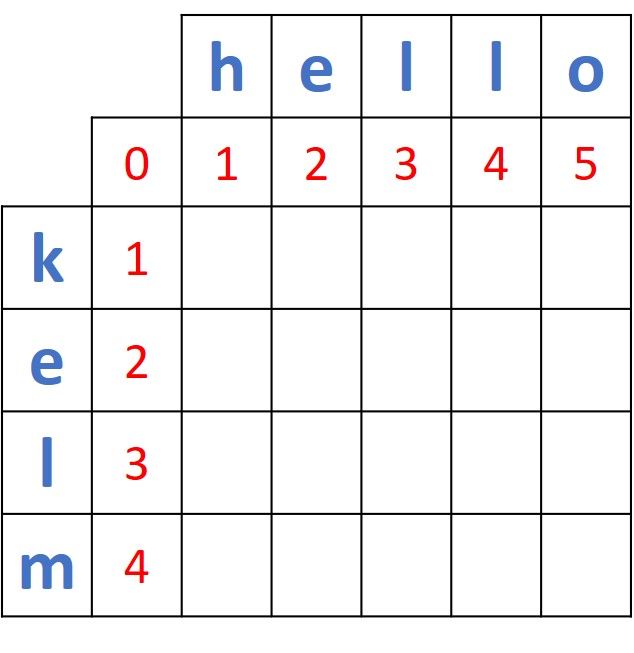
The first step is to initialize a distance matrix as given in the next table. Excluding the row and column used as labels, the matrix size is 5 x 6. The number of rows, 5, equals the number of characters in the first (4) word +1. The same happens for the number of columns.

The value that represents the distance between the 2 words is the value located at the bottom-right corner of the matrix located in the fifth row (index 4, starting from 0) and the sixth column (index 5).

The extra row and column of that matrix hold numbers starting from 0 and incremented by 1. Why add such an extra row and column?

The short answer is that adding the extra row and column helps to apply dynamic programming to calculate the distance. Now let's discuss the long answer.

Remember that dynamic programming is about breaking a complex problem down into a number of simple problems. In our case, the complex problem is calculating the Levenshtein distance by filling the above matrix. What about the simple problem?

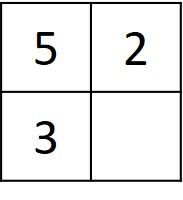
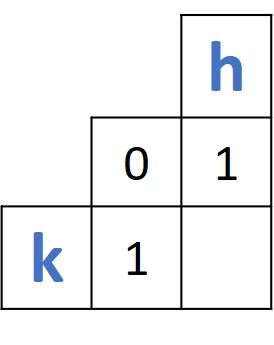
The simple problem is to work with only a matrix of size 2 x 2, similar to the one given below. Due to initializing the left-most column and the top row with numbers starting from 0, there will be always three already-existing elements and only one missing element, which will always be the one corresponding to the bottom-right corner.

The value of the missing element could be calculated according to one of these two options (based on whether the two prefixes being compared are similar or not):

1. The minimum of the 3 existing elements : min(5, 2, 3)=2. In case the 2 prefixes are identical.
2. The minimum of the 3 existing elements + 1 : min(5, 2, 3) + 1 = 2 + 1 = 3. In case the 2 prefixes are different.

In case the 2 prefixes are identical, then there is nothing to do and thus no additional cost is added. When the prefixes are different, there is an operation to be applied (insertion, deletion, or substitution). This is why there is an additional cost of 1 to be added.

By calculating all missing elements that way, the entire distance matrix will be calculated.

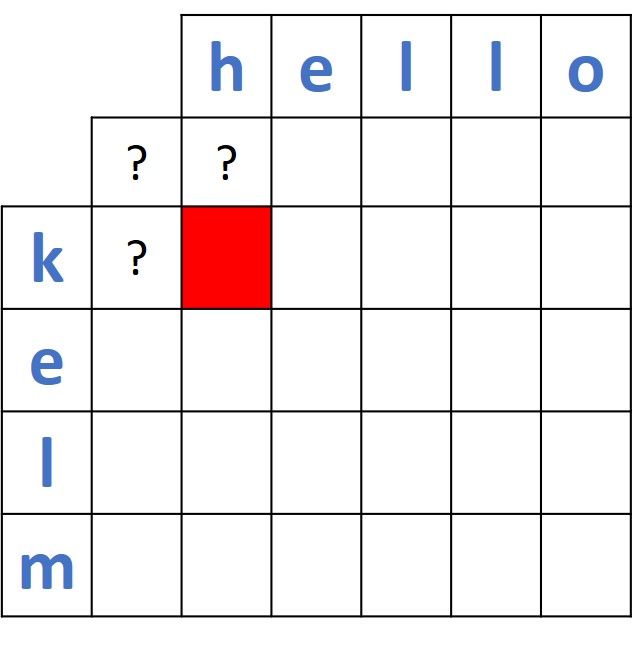
Back to our question which is why we add the additional row and column in the distance matrix. Assume that the distance is to be calculated between the first 2 prefixes of the 2 words which are (k and h). According to the dynamic programming approach explained above, there must be three known values and just one missing value (marked in red in the next figure). By comparing the 3 existing values, the forth value will be calculated.

If the additional row and column are not existing, then there will be 4 unknown values and the previous approach will not be applicable in this case. If such row and column exist, then there will be just 1 missing value and this is what expected to solve the problem using dynamic programming.

After clarifying the purpose of the additional row and column in the matrix, it's time to fill the distance matrix to reach the value that represents the distance between the 2 words.

Step-by-Step Calculation of the Levenshtein Distance Using Dynamic Programming

In this section, the distance matrix will be filled in order to find the distance between the 2 words which is located in the bottom-right corner.

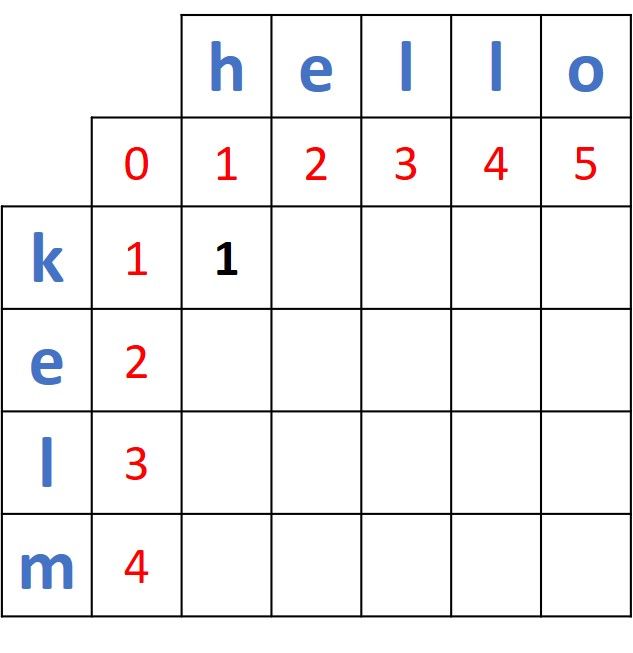
The first distance to be calculated is between the first two prefixes of the two words, which are k and h. The 2 x 2 matrix involved in this operation is given in the next figure. Because the two prefixes are different, the distance between them is calculated as the minimum of the 3 existing values (0, 1, and 1) + 1. So, the distance is min(0, 1, 1) + 1 = 0 + 1 = 1.

The distance matrix is updated by each calculated distance. The current matrix is given below.

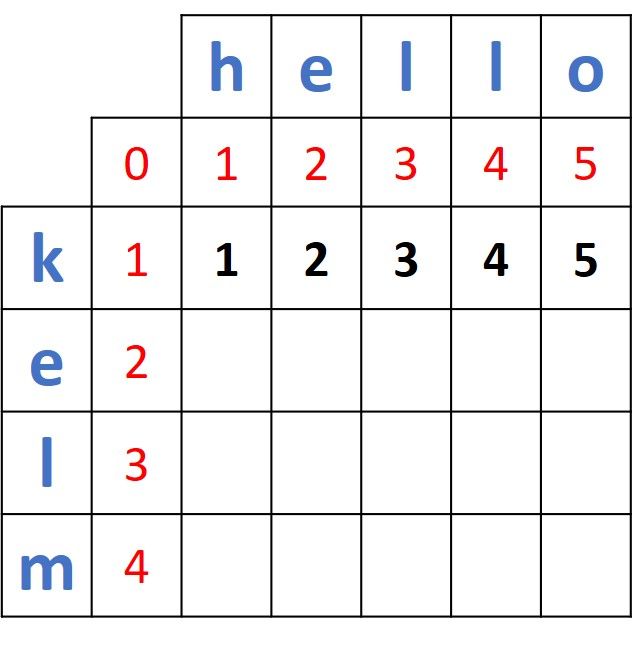
Let's calculate the distance between the first prefix of the first word, k, and the second prefix for the second word, he. As discussed previously, the distance is 2, and for the next prefixes we just add one to get a distance of 3, 4, and 5. Here is the distance matrix after being updated with these distances.

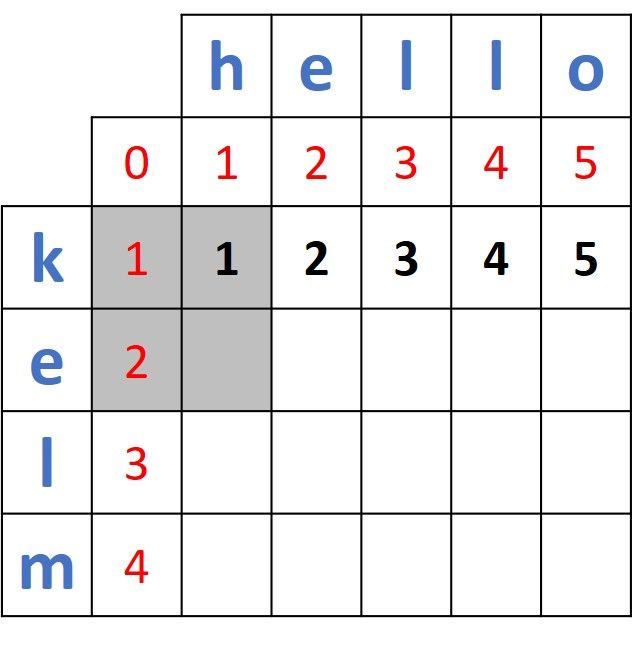
After filling the row corresponding to the prefix k of the word kelo, next we'll fill the second row which corresponds to the second prefix: ke. Note that the label in the second row is just e, not ke but it implies ke. For example, the first missing value in the second row means the distance to transform ke into h, the second one means the distance to transform ke into he, the third mean the distance to transform ke into hel, and so on. The reason is that the distances between e and the prefixes in the word hello are calculated based on the distances calculated for the prefix k.

For calculating the distance between e and h, then the 2x2 matrix that will be used is highlighted according to the next figure. Because the prefixes e and h are different, then the resultant distance equals min(1, 1, 2) + 1 = 1 + 1 = 2.

Here is the new matrix after adding the recently calculated distance.

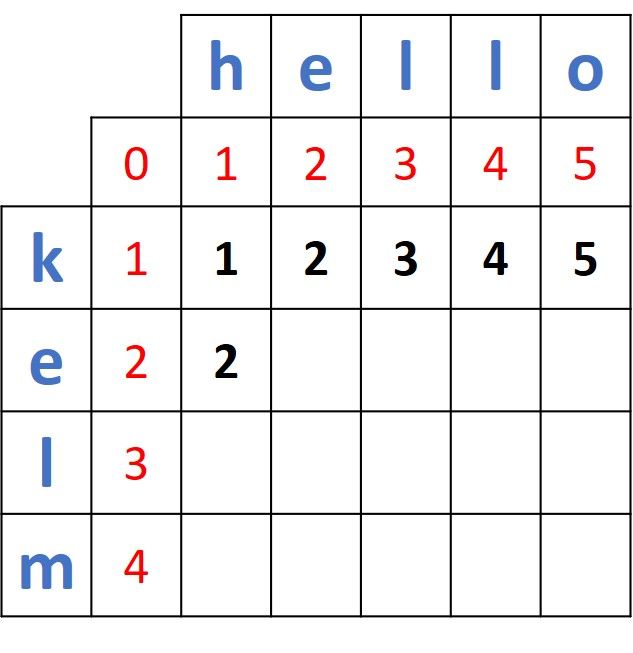
Moving to compare e (from the first word) and e (from the second word), here is the highlighted 2x2 matrix.

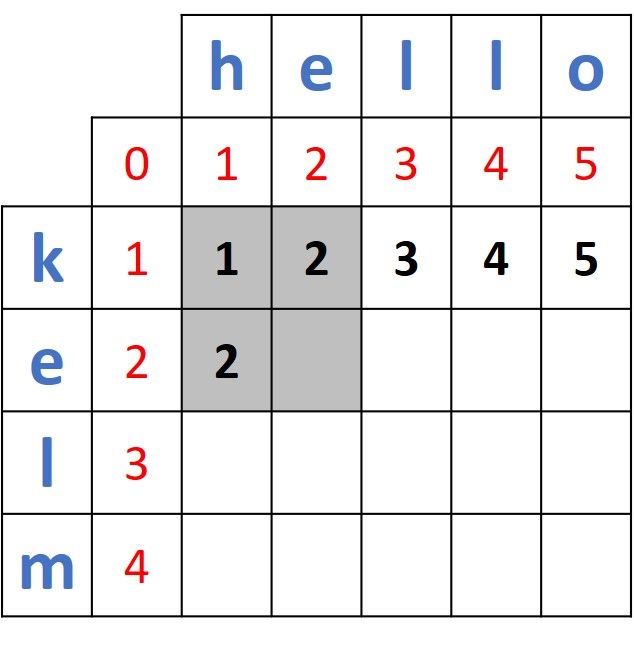
Because the 2 sides (e and e) are identical, then the distance will be calculated as just the minimum of the 3 existing values in the 2x2 matrix. Thus, the result is min(1, 2, 2) = 1. The next figure shows the matrix after being updated by the newly calculated distance.

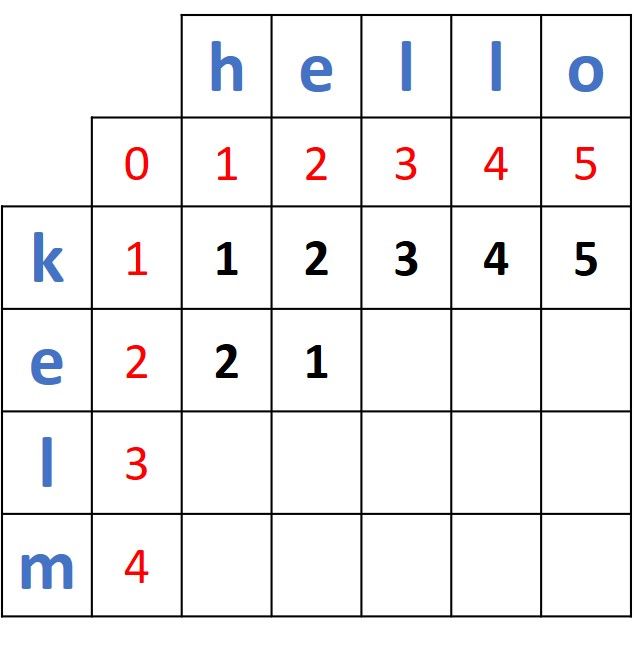
The process continues until all of the cells are filled for the row corresponding to "e".

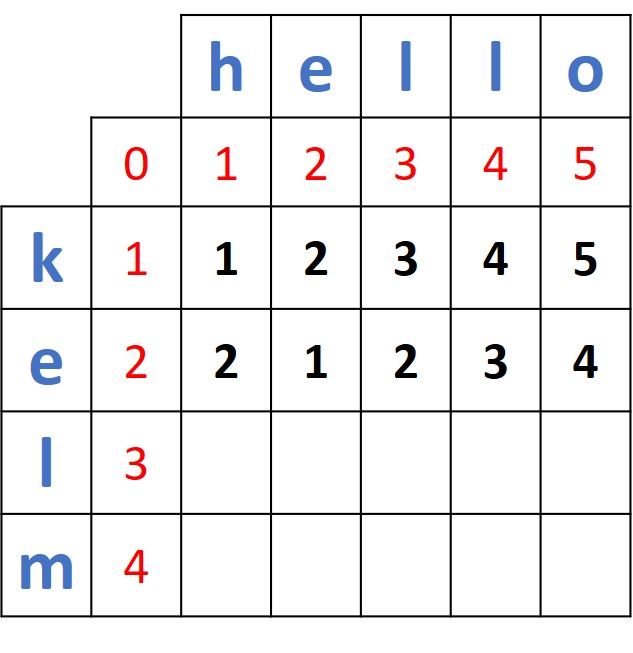
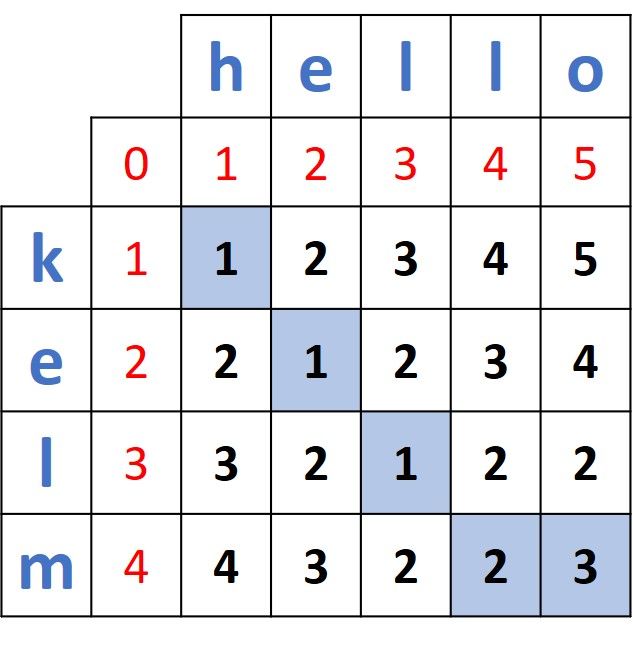
Continuing in this way, the complete distance matrix is shown below. The distance between the two full words kelm and hello is located at the bottom-right corner and the path of distances is marked in blue. The bottom-right cell has a value 3 which means 3 edits are required to transform kelm into hello. The 3 edits are:

1. Substitution of k by h.
2. Substitution of m by l.
3. Inserting o.

This marks the end of this example.

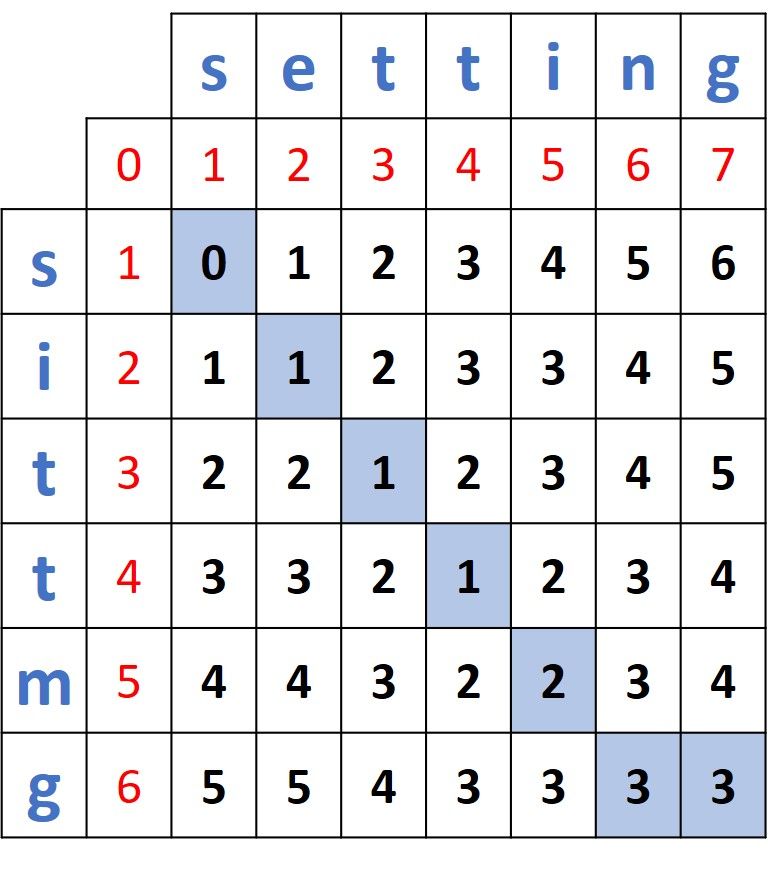
Without showing the steps, here is another distance matrix for measuring the distance between the words sittmg and setting.

Conclusion

This tutorial discussed the Levenshtein distance for measuring the distance between two words by counting the number of single-character edits required to transform one word into another. The three possible edits are insertion, deletion, and substitution.

By working through an example, the detailed steps for calculating the distance matrix using dynamic programming are made clear. The problem is divided into small problems of calculating the minimum of a 2 x 2 matrix.

In the next next post we'll see how to implement the Levenshtein distance using Python.