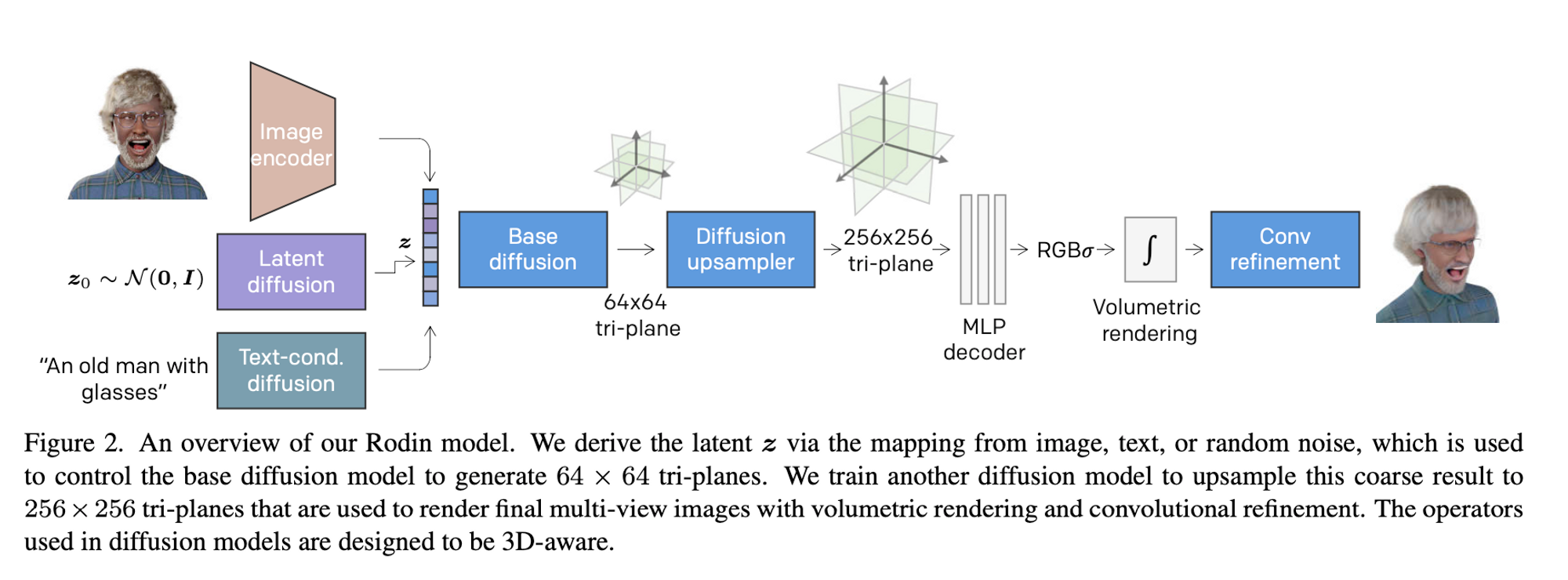
Overview
Rodin is a diffusion model that represents 3D avatars as neural radiance fields which can then be rendered using volumetric rendering techniques which are common to NeRFs. This solution was proposed in order to counter the large memory and computation costs associated with producing high-quality photorealistic avatars.
Rodin represents a NeRF as multiple 2D feature maps and rolls out these maps into a single feature plane which they use to perform 3D-aware diffusion. Specifically, they use tri-plane representation which represents a volume by three axis-aligned orthogonal feature planes. This representation is possible because of:
- 3D-aware convolution. This 3D-aware convolution explicitly accounts for the fact that a 2D feature in one plane (of the tri-plane) is a projection from a piece of 3D data and is intrinsically associated with the same data’s projected features in the other two planes.
- Latent Conditioning. In order to ensure that the features of the training data are globally coherent across the 3D volume, they use latent codes for feature generation. This leads to better-quality avatars and enables semantic editing using text or image data.
- Hierarchical Synthesis. The diffusion models generate low-resolution triplane features which are then upsampled into higher-quality features which can then be rendered into the 3D avatar.
How Do They Build The Model?
In order to train this model, they:
- Collect a dataset of 3D-rendered avatars using the Blender synthetic pipeline.
- For each avatar, they fit the volumetric neural representation which is used to explain the observations for each avatar
- They use diffusion models to characterize the distribution of these 3D instances.
- They use 2 diffusion models: one that generates coarse geometry and another one that upsamples the coarse geometric info into high-resolution synthetic avatars.
I will elaborate more on these steps in the following paragraphs.
PART 1: Robust 3D Representation Fitting
There was a need to create an expressive 3D representation that accounts for multi-view images that meet the following criteria:
- It needs to be amenable to generative network processing
- It needs to be compact enough to be considered memory efficient
- It needs to be computed fast enough to minimize the time required for optimization
The authors settle on tri-plane representation to model the neural radiance field of 3D avatars. In this representation, the 3D volume is factorized into three axis-aligned orthogonal feature planes, denoted by $y_{uv},y_{wu},y_{vw} \in RH\times W\times C,$ each of which has a spatial resolution of H × W and number of channels as C.
With this encoding, “rich 3D information is explicitly memorized in the tri-plane features, and one can query the feature of the 3D point $p \in R3$ by projecting it onto each plane and aggregating the retrieved features, i.e., $yp = y_{uv}(p_{uv}) + y_{wu}(p_{wu}) + y_{vw}(p_{vw})$.” (paper) Given this positional information, it is possible for an MLP decoder to predict the density and view-dependent color for each viewing direction.
Using a mean squared error (MSE) loss function the tri-plane features and MLP decoder are optimized such that the rendering of the neural radiance field matches the multi-view images for the given subject. To reduce the presence of artifacts in the rendered images, they use sparse, smooth, and compact regularizers.
This 3D fitting procedure considers a few factors to measure success:
- The tri-plane features of different subjects should reside in the same domain. To do this, they adopt a shares MLP decoder when fitting distinct portraits pushing the tri-plane features to the shared latent space that is recognized by the decoder
- The MLP decoder has to possess some level of robustness in order to accommodate slight noise and varied resolutions of the tri-plane features. To achieve this they randomly scale the tri-plane during model fitting.
PART 2: Latent Conditioned 3D Diffusion
Diffusion Model Recap:
Diffusion models work by gradually reversing a Markov chain. During the forward process of the Markov chain, the diffusion model adds a linear amount of Gaussian noise to the input data. During the reverse (denoising) chain, the diffusion model learns to predict the amount of noise in the data and remove it based on the noise scheduler. The diffusion model is parameterized to predict the amount of added noise. During inference, the diffusion sampler starts from input data of 100% noise and sequentially produces less noisy samples. Now that we’ve revised diffusion models, let’s see how they factor into the Rodin architecture.
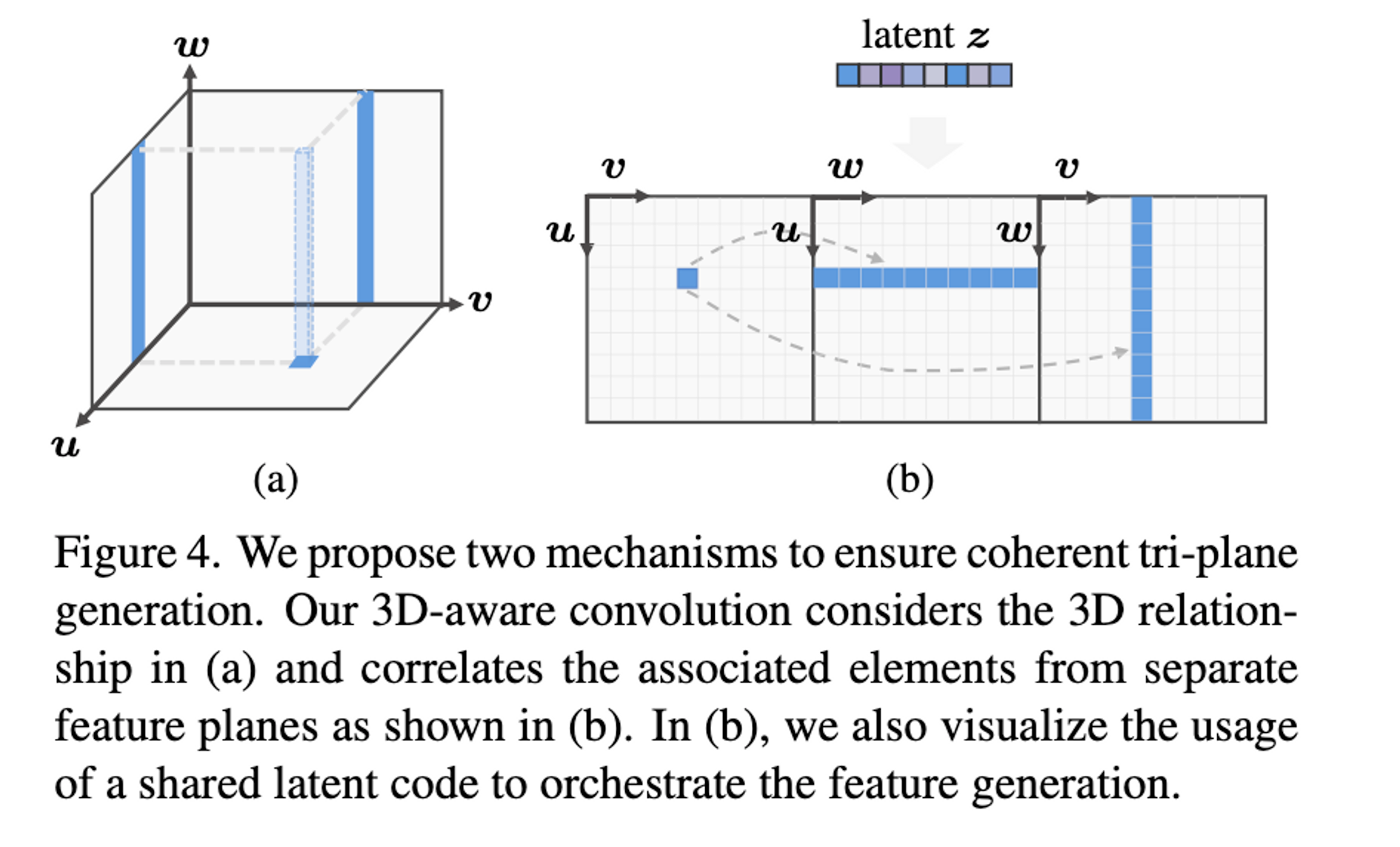
After they train a NeRF model in part 1, they go ahead and train a diffusion model to generate the tri-plane features which were manually created in part 1. The base diffusion model is tasked with generating coarse-level tri-planes at $64 \times 64$ resolution. They “roll out” the tri-plane features by concatenating the tri-plane features horizontally, yielding $y = hstack(y_{uv},y_{wu},y_{vw}) \in R^{H \times W \times 3C}$. A point on a certain feature plane actually corresponds to an axis-aligned 3D line in the volume, which has two corresponding line projections in other planes. This roll-out allows independent processing of feature planes. We need an architecture that is able to process the tri-plane roll-out as opposed to standard 2D input. In order to train a diffusion model on 3D data they implement, “3D aware convolution” to effectively process the tri-plane features while respecting their 3D relationship. This 3D-aware convolution explicitly attaches the features of each plane to the corresponding row/column of the rest of the planes. Basically, the information of each other 2 planes is encoded in the current plane for each plane and vice versa.
Latent Conditioning
Because Rodin is a diffusion model that learns to generate tri-plane features, they train an image encoder to extract a semantic latent vector serving as the conditional input of the base diffusion model. They only extract the latent vector from the frontal view of each training subject and the diffusion model conditioned on the latent vector is trained to reconstruct the tri-plane of the same subject.
During training, the latent guide is zeroed out 20% of the time for classifier-free guidance. This allows the final trained model to function with or without latent guides.
PART 3: Diffusion Tri-plane Upsampler
In part 2, we train a base diffusion model to generate the coarse-level tri-plane e.g. at $64\times 64$ resolution. In part 3, we further train a separate diffusion model to increase the tri-plane resolution to $256\times 256.$ This upsampler diffusion model is conditioned on the low-resolution tri-plane output from the base diffusion model. As opposed to the base diffusion model that predicts the amount of noise in the input data at each denoising step, the upsampler predicts the high-resolution ground truth as opposed to the amount of noise added.
They apply condition augmentation to reduce the domain gap between the output from the base model and the low-resolution conditional training for the upsampler training. They also augment the input tri-plane data by applying Gaussian blurring and Gaussian noises.
The upsampler is optimized by $l_2$ loss and perceptual loss computed via a pre-trained VGG model that evaluates random patches of the rendered image. In addition to this, they train a convolution refiner which complements the missing details of the NeRF rendering.
Summary
Rodin is a merge of a diffusion model and a NeRF model. The authors have achieved a high-resolution model for generating 3D avatars which use low computing and memory costs. The other admirable part of this model is the modularity of the model which allows the user to interchange various pieces of the architecture based on their preferences. At the writing of this article, the code is not yet publicly available but the individual components of the model can be morphed together from pre-existing NeRF and diffusion models.










