Concurrent Spatial and Channel Squeeze & Excitation (scSE) Nets

Squeeze-and-Excitation Networks have been a stronghold method of applying attention mechanisms in computer vision since their inception. However, they do have certain drawbacks which have been continuously addressed by other researchers in some form. In this article, we are going to talk about one such paper accepted to MICCAI 2018 by Roy et. al. titled "Concurrent Spatial and Channel Squeeze & Excitation in Fully Convolutional Networks". The paper revolves around introducing a Spatial Attention branch to the Squeeze-and-Excitation module which is similar to that of the Convolutional Block Attention Module (CBAM), with, however, a slight difference in the way the channel and spatial attention is aggregated.

Without further ado, let's dive into the motivation of scSE followed by an analysis of the structural design of the module, and then finally wrap it up by investigating the results observed along with its PyTorch code.

Table of Contents

1. Motivation
2. scSE Module
3. Code
4. Results
5. Conclusion
6. References

Abstract

Fully convolutional neural networks (F-CNNs) have set the state-of-the-art in image segmentation for a plethora of applications. Architectural innovations within F-CNNs have mainly focused on improving spatial encoding or network connectivity to aid gradient flow. In this paper, we explore an alternate direction of recalibrating the feature maps adaptively, to boost meaningful features, while suppressing weak ones. We draw inspiration from the recently proposed squeeze & excitation (SE) module for channel recalibration of feature maps for image classification. Towards this end, we introduce three variants of SE modules for image segmentation, (i) squeezing spatially and exciting channel-wise (cSE), (ii) squeezing channel-wise and exciting spatially (sSE) and (iii) concurrent spatial and channel squeeze & excitation (scSE). We effectively incorporate these SE modules within three different state-of-the art F-CNNs (DenseNet, SD-Net, U-Net) and observe consistent improvement of performance across all architectures, while minimally effecting model complexity. Evaluations are performed on two challenging applications: whole brain segmentation on MRI scans and organ segmentation on whole body contrast enhanced CT scans.

Motivation

Squeeze-and-Excitation modules have been instrumental in the field of computer vision. A deep convolutional neural network architecture equipped with Squeeze-and-Excitation modules won first place in the ILSVRC 2017 classification competition on the ImageNet dataset, which set the tone for further enhanced exploration of more variants of channel attention modules. The intuition behind Squeeze-and-Excitation modules or channel attention, in general, is somewhat inherited from human visual cognitive abilities in the scope of focusing on more important objects in a scene. In this paper, the authors were inspired to leverage the high performance of Squeeze-and-Excitation blocks for image classification and image segmentation with Fully Convolutional Neural Networks (F-CNNs), primarily in the domain of medical image segmentation. Since medical image segmentation demands attention on the spatial domain as well, the authors extend the structural design of SE (which is denoted as cSE, where the c stands for the "channel", since SE is a channel-exclusive excitation operator) by including a concurrent spatial attention block.

Corollary to the success of Squeeze-and-Excitation channel descriptors, the authors first propose an alternative version of the SE block which "'squeezes' along the channels and 'excites' spatially, termed spatial SE (sSE)". Subsequently, the authors introduce a mix of the conventional SE and sSE blocks called concurrent spatial and channel SE blocks (scSE) that "recalibrate the feature maps separately along channel and space and then combine the output". The goal is to essentially maximize information propagation into the attention mechanism so that the focus can be simultaneously at a pixel level and at a channel level. Although the scSE block was primarily introduced in this paper for Fully Convolutional Neural Networks (F-CNNs), like UNets and DenseNets, the method can be applied/inserted into conventional CNN-based architectures like Residual Networks. The paper also heavily investigates the role of these SE-based blocks in the case of medical image segmentation, which serves as a primary motivation to provide spatial per-pixel level attention since, as in the case of medical image segmentation, per-pixel information is extremely crucial as compared to the channel-level information because of the usual format of the data (.dicom).

scSE Module

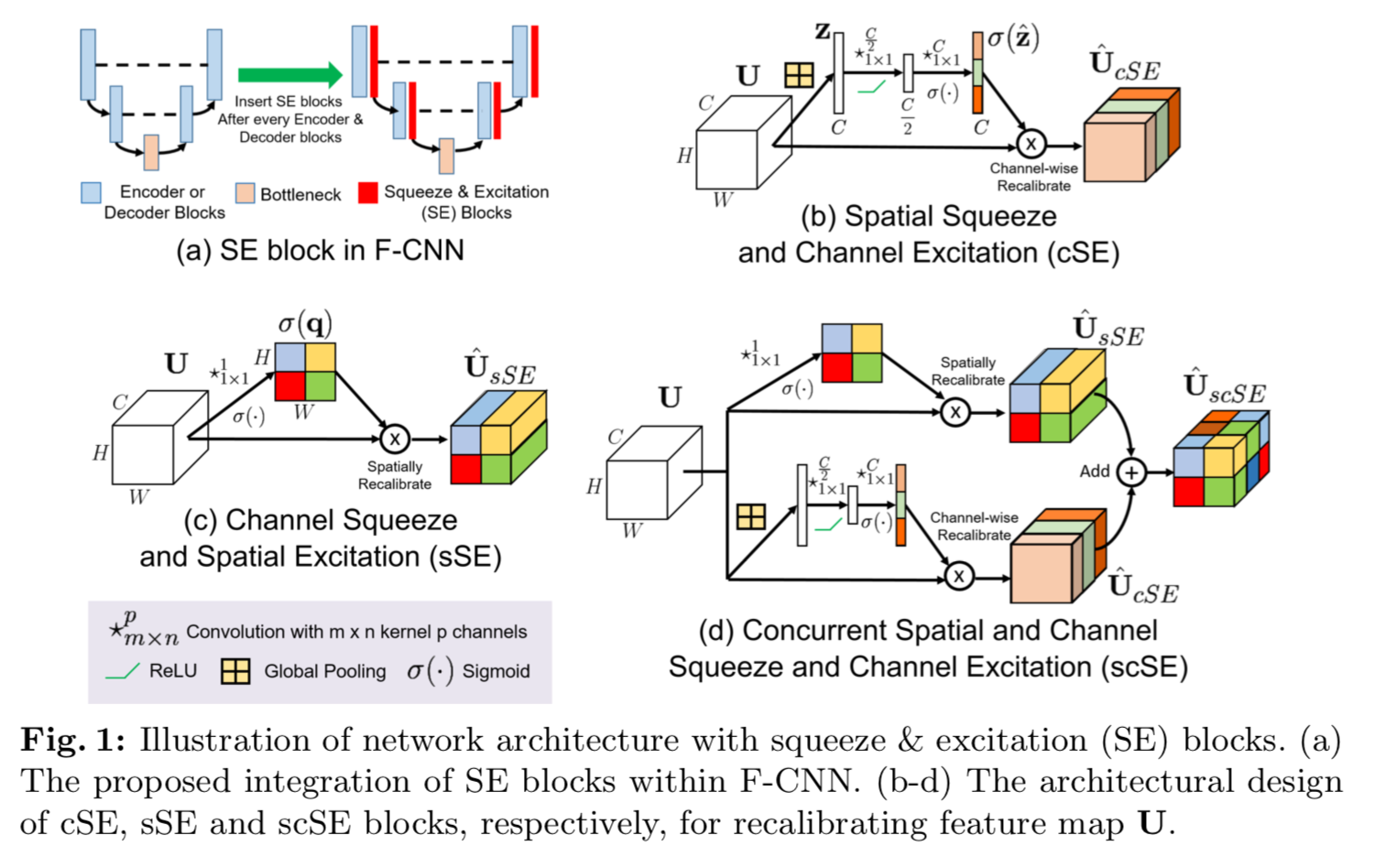
There are three components to dissect here, as shown in the above diagram taken from the paper:

• Spatial Squeeze and Channel Excitation (cSE)
• Channel Squeeze and Spatial Excitation (sSE)
• Concurrent Spatial and Channel Squeeze and Channel Excitation (scSE)

Spatial Squeeze and Channel Excitation (cSE)

Essentially, this denotes the conventional Squeeze-and-Excitation block. The SE block is made up of 3 modules which are the squeeze module, excitation module, and scaling module. Let's assume the input to this cSE block is a 4-dimensional feature map tensor $\textbf{X} \in \mathbb{R}^{N \ast C \ast H \ast W}$, where $N \ast C \ast H \ast W$ represents the batch size, number of channels and the spatial dimensions (height and width of the individual feature maps/ channels respectively), then, the squeeze module reduces $\textbf{X}$ to $\tilde{\textbf{X}} \in \mathbb{R}^{N \ast C \ast 1 \ast 1}$ by using the Global Average Pooling (GAP). This is done to ensure the computational complexity is significantly lower as compared to computing the attention weights over the full-sized input tensor $\textbf{X}$. Further, $\tilde{\textbf{X}}$ is passed as the input to the excitation module which passes this reduced tensor through a Multi-layered perceptron (MLP) bottleneck. This outputs the resultant tensor $\hat{\tilde{\textbf{X}}}$ which is of the same dimension as that of $\tilde{\textbf{X}}$. Lastly, the scaling module applies a sigmoid activation unit to this tensor $\hat{\tilde{\textbf{X}}}$ which is then element wise multiplied with the original input tensor $\textbf{X}$.

To understand the functionalities of Squeeze-and-Excitation Networks in more details, head over to our detailed article on SENets.

Channel Squeeze and Spatial Excitation (sSE)

Complimentary to cSE, sSE is essentially a sort of reverse to it's counterpart which reduces the feature tensor over the spatial dimension and excites over the channel dimension. Contrary to it, sSE squeezes the channels and excites over the spatial dimension. Similar to cSE, let's assume the input to this cSE block is a 4-dimensional feature map tensor $\textbf{X} \in \mathbb{R}^{N \ast C \ast H \ast W}$. Firstly, the input tensor $\textbf{X}$ is reduced to $\tilde{\textbf{X}} \in \mathbb{R}^{N \ast 1 \ast H \ast W}$ by a 2D pointwise convolutional kernel which reduces the $C$ channels to 1. Lastly, this compressed tensor $\tilde{\textbf{X}}$ is passed through a sigmoid activation unit and then element wise multiplied with the original input tensor $\textbf{X}$.

Concurrent Spatial and Channel Squeeze and Channel Excitation (scSE)

Simply put, scSE is an amalgamation of the previously discussed cSE and sSE blocks. Firstly, similar to both cSE and sSE, let's assume the input to this cSE block is a 4-dimensional feature map tensor $\textbf{X} \in \mathbb{R}^{N \ast C \ast H \ast W}$. This tensor $\textbf{X}$ is passed in parallel through both cSE and sSE blocks. The two resultant outputs are then element wise summed up to provide the final output. However, there are extensions were researchers and users alike have found out that instead of doing element wise summation, computing an element wise max over the two tensors is also a desirable strategy and provides competitive and comparable results as compared to the original scSE variant as described by the authors in the paper.

Code

The following snippet provides the PyTorch code for the scSE, cSE and sSE blocks which can be easily inserted into the blocks of any conventional convolutional neural network architecture in the domain of computer vision.

import torch
import torch.nn as nn
import torch.nn.functional as F


class ChannelSELayer(nn.Module):
    """
    Re-implementation of Squeeze-and-Excitation (SE) block described in:
        *Hu et al., Squeeze-and-Excitation Networks, arXiv:1709.01507*
    """

    def __init__(self, num_channels, reduction_ratio=2):
        """
        :param num_channels: No of input channels
        :param reduction_ratio: By how much should the num_channels should be reduced
        """
        super(ChannelSELayer, self).__init__()
        num_channels_reduced = num_channels // reduction_ratio
        self.reduction_ratio = reduction_ratio
        self.fc1 = nn.Linear(num_channels, num_channels_reduced, bias=True)
        self.fc2 = nn.Linear(num_channels_reduced, num_channels, bias=True)
        self.relu = nn.ReLU()
        self.sigmoid = nn.Sigmoid()

    def forward(self, input_tensor):
        """
        :param input_tensor: X, shape = (batch_size, num_channels, H, W)
        :return: output tensor
        """
        batch_size, num_channels, H, W = input_tensor.size()
        # Average along each channel
        squeeze_tensor = input_tensor.view(batch_size, num_channels, -1).mean(dim=2)

        # channel excitation
        fc_out_1 = self.relu(self.fc1(squeeze_tensor))
        fc_out_2 = self.sigmoid(self.fc2(fc_out_1))

        a, b = squeeze_tensor.size()
        output_tensor = torch.mul(input_tensor, fc_out_2.view(a, b, 1, 1))
        return output_tensor


class SpatialSELayer(nn.Module):
    """
    Re-implementation of SE block -- squeezing spatially and exciting channel-wise described in:
        *Roy et al., Concurrent Spatial and Channel Squeeze & Excitation in Fully Convolutional Networks, MICCAI 2018*
    """

    def __init__(self, num_channels):
        """
        :param num_channels: No of input channels
        """
        super(SpatialSELayer, self).__init__()
        self.conv = nn.Conv2d(num_channels, 1, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, input_tensor, weights=None):
        """
        :param weights: weights for few shot learning
        :param input_tensor: X, shape = (batch_size, num_channels, H, W)
        :return: output_tensor
        """
        # spatial squeeze
        batch_size, channel, a, b = input_tensor.size()

        if weights is not None:
            weights = torch.mean(weights, dim=0)
            weights = weights.view(1, channel, 1, 1)
            out = F.conv2d(input_tensor, weights)
        else:
            out = self.conv(input_tensor)
        squeeze_tensor = self.sigmoid(out)

        # spatial excitation
        squeeze_tensor = squeeze_tensor.view(batch_size, 1, a, b)
        output_tensor = torch.mul(input_tensor, squeeze_tensor)
        return output_tensor


class ChannelSpatialSELayer(nn.Module):
    """
    Re-implementation of concurrent spatial and channel squeeze & excitation:
        *Roy et al., Concurrent Spatial and Channel Squeeze & Excitation in Fully Convolutional Networks, MICCAI 2018, arXiv:1803.02579*
    """

    def __init__(self, num_channels, reduction_ratio=2):
        """
        :param num_channels: No of input channels
        :param reduction_ratio: By how much should the num_channels should be reduced
        """
        super(ChannelSpatialSELayer, self).__init__()
        self.cSE = ChannelSELayer(num_channels, reduction_ratio)
        self.sSE = SpatialSELayer(num_channels)

    def forward(self, input_tensor):
        """
        :param input_tensor: X, shape = (batch_size, num_channels, H, W)
        :return: output_tensor
        """
        #output_tensor = torch.max(self.cSE(input_tensor), self.sSE(input_tensor))
        output_tensor = self.cSE(input_tensor) + self.sSE(input_tensor)
        return output_tensor

Results

The following results as provided in the paper showcase the efficacy of the scSE block used in different F-CNN architectures like U-Net, SD-Net and DenseNets on the MALC and Visceral Datasets for Medical Image Segmentation.

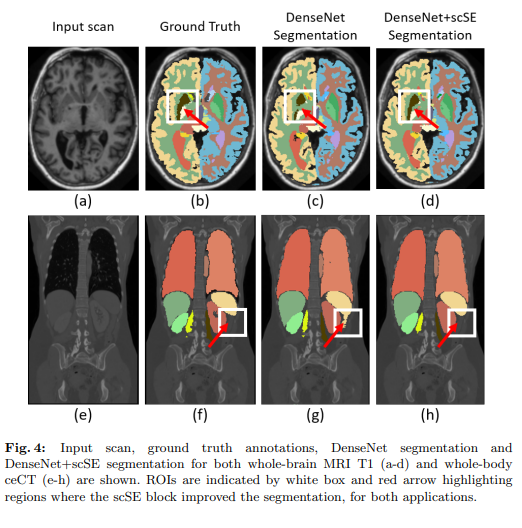
Conclusion

scSE blocks were the first approach to successfully show the importance and benefits of applying channel wise and per-pixel attention operators in F-CNNs models. The results showcased are promising, however, are considerably computationally expensive due to the sSE branch applied. However, it boils down to the users giving it a try on their own dataset to understand the actual efficiency of the block in terms of the accuracy boost it provides as compared to the computational overhead added.

References

1. Concurrent Spatial and Channel ‘Squeeze & Excitation’ in Fully Convolutional Networks
2. scSE code
3. Channel Attention and Squeeze-and-Excitation Networks (SENet), Paperspace Blog