Shuffle Attention for Deep Convolutional Neural Networks (SA-Net)

If a deep learning researcher from the previous decade traveled through time to today and asked what topic most current research is focused on, it could be said with a high degree of confidence that Attention Mechanisms would be on the top of that list. Attention mechanisms have reigned supreme both in Natural Language Processing (NLP) and Computer Vision (CV). While in NLP, the focus has been on making transformer-esque architectures more efficient, in the case of CV, it has been more on plug-and-play modules to push the SOTA.

The paper that is the topic of this article serves the same purpose. We are talking about the ICASSP 2021 paper titled SA-Net: Shuffle Attention for Deep Convolutional Neural Networks.

The paper proposes a novel attention mechanism known as Shuffle Attention, which can be used in conventional backbones to improve performance at a minimal computational cost. In this article, we are going to kick off the ritual by discussing the motivation behind Shuffle Attention, followed by a structural dissection of the network, before we close the article with the results presented in the paper along with its code.

Table of Contents

1. Motivation
2. Shuffle Attention
3. Code
4. Results
5. Conclusion
6. References

Paper Abstract

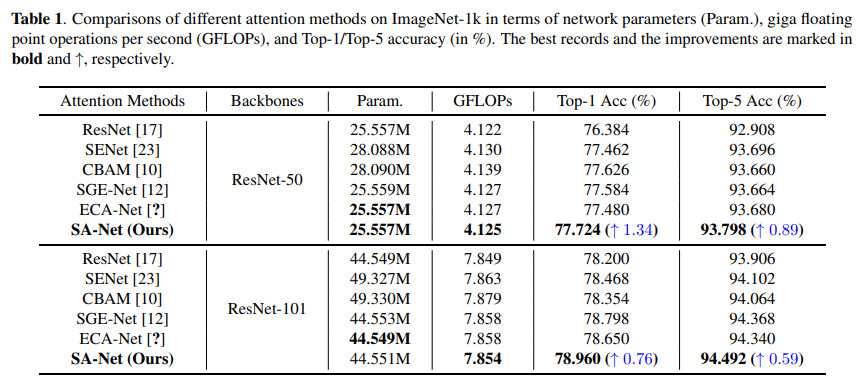
Attention mechanisms, which enable a neural network to accurately focus on all the relevant elements of the input, have become an essential component to improve the performance of deep neural networks. There are mainly two attention mechanisms widely used in computer vision studies, spatial attention and channel attention, which aim to capture the pixel level pairwise relationship and channel dependency, respectively. Although fusing them together may achieve better performance than their individual implementations, it will inevitably increase the computational overhead. In this paper, we propose an efficient Shuffle Attention (SA) module to address this issue, which adopts Shuffle Units to combine two types of attention mechanisms effectively. Specifically, SA first groups channel dimensions into multiple sub-features before processing them in parallel. Then, for each sub-feature, SA utilizes a Shuffle Unit to depict feature dependencies in both spatial and channel dimensions. After that, all sub-features are aggregated and a “channel shuffle” operator is adopted to enable information communication between different sub-features. The proposed SA module is efficient yet effective, e.g., the parameters and computations of SA against the backbone ResNet50 are 300 vs. 25.56M and 2.76e-3 GFLOPs vs. 4.12 GFLOPs, respectively, and the performance boost is more than 1.34% in terms of Top-1 accuracy. Extensive experimental results on commonly used benchmarks, including ImageNet-1k for classification, MS COCO for object detection, and instance segmentation, demonstrate that the proposed SA outperforms the current SOTA methods significantly by achieving higher accuracy while having lower model complexity.

Motivation

Attention mechanisms have caught the eye of many researchers in the field of deep learning over the last few years and have been dominating the scene in today's research communities. In computer vision (mostly in the domains of image classification and object recognition), plug-and-play modules like Squeeze-and-Excitation Networks have served as the foundation for many more attention mechanisms to follow. Ranging from CBAM to ECA-Net, the goal has been to provide a low-cost module to add more representative power to improve the performance of deep convolutional neural networks. Most of these attention mechanisms are divided into two different categories: Channel Attention and Spatial Attention. The former aggregates the features across the channel dimension of the feature map tensor, while the latter aggregates the information across the spatial dimension of each channel in the feature map tensor. However, these types of attention mechanisms do not take full advantage of the correlation between spatial and channel attention, which makes them less efficient.

This paper aims to answer the following question:

Can one fuse different attention modules in a lighter but more efficient way?

The authors answer the above question by taking inspiration from three fundamental concepts:

1. Multi-Branch Architecture
2. Grouped Features
3. Attention Mechanisms

Multi-Branch Architecture

The authors take inspiration from the popular ShuffleNet v2 architecture which efficiently constructed a multi-branch structure and processes different branches in parallel. Precisely, the input is split into two branches each with $\frac{c}{2}$ channels, where $c$ is the total number of channels. These two branches then go through subsequent layers of convolution before being merged by concatenation to form the final output.  

Grouped Features

The authors rely on the idea of the Spatial Group-wise Enhance (SGE) attention mechanism, which introduced a grouping strategy that divides the input feature map tensor into groups along the channel dimension. These groups are then enhanced in parallel with a series of operations.

Attention Mechanisms

Less of an inspiration and more of a literature review, the authors review current existing attention mechanisms which combined channel and spatial attention sequentially like CBAM, GCNet and SGE.

Shuffle Attention

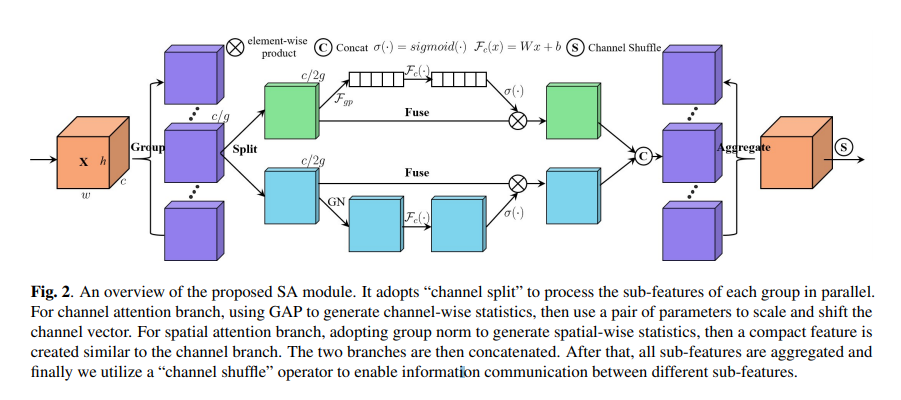
Consider Shuffle Attention to be a hybrid between SE channel attention, spatial attention from CBAM, and channel grouping from SGE. There are four components of Shuffle Attention:

1. Feature Grouping
2. Channel Attention
3. Spatial Attention
4. Aggregation

Feature Grouping

The feature grouping property in Shuffle Attention (SA) is a two-level hierarchy. Assuming the input tensor to the attention module to be $\textbf{X} \in \mathbb{R}^{C \ast H \ast W}$, where $C$ denotes the channel dimension and $H \ast W$ denotes the spatial dimensions of each feature map, then SA first divides $\textbf{X}$ into $G$ groups along the channel dimension such that each group now becomes $\tilde{\textbf{X}} \in \mathbb{R}^{\frac{C}{G} \ast H \ast W}$. These feature groups are then passed to the attention modules where they are further divided into two groups along the channel dimension, each for the spatial and channel attention branch. Thus, the sub-feature group which is passed through each of the spatial or channel attention branches can be denoted by $\hat{\textbf{X}} \in \mathbb{R}^{\frac{C}{2G} \ast H \ast W}$.

Channel Attention

For channel attention branch, SA first reduces $\hat{\textbf{X}}$ to ${\frac{C}{2G} \ast 1 \ast 1}$ by applying a Global Average Pooling (GAP) layer. A simple gating mechanism is applied using a compact feature created to enable guidance for precise and adaptive selection, which is followed by a sigmoid activation function. This can be represented by the following mathematical formula:

$$ X^{\prime}_{k1} = \sigma(\mathcal{F}_{c}(s)) \cdot \hat{\textbf{X}} = \sigma(W_{1s}+b_{1}) \cdot \hat{\textbf{X}} $$

Where $W_{1} \in \mathbb{R}^{\frac{C}{2G} \ast 1 \ast 1}$ and $b_{1} \in \mathbb{R}^{\frac{C}{2G} \ast 1 \ast 1}$ are parameters used to scale and shift the GAP($\hat{\textbf{X}}$).

Spatial Attention

For Spatial Attention, the input $\hat{\textbf{X}}$ is reduced by the Group Norm to obtain the spatial-wise statistics. Subsequently, $\mathcal{F}_{c}(\cdot)$ is used to enhance the representation of the reduced tensor. This can be represented by the following mathematical equation:

$X^{\prime}_{k2} = \sigma(W_{2} \cdot GN(\hat{\textbf{X}}) + b_2) \cdot \hat{\textbf{X}}$

Aggregation

The outputs of the Spatial Attention and Channel Attention branches are first concatenated. Post concatenation, similar to ShuffleNet v2, a channel shuffle strategy is adopted to enable cross-group information flow along the channel dimension. Thus the final output is of the same dimension as that of the input tensor to the SA layer.

Code

The following code snippet provides the structural definition of the SA layer in PyTorch.

import torch
import torch.nn as nn
from torch.nn.parameter import Parameter


class sa_layer(nn.Module):
    """Constructs a Channel Spatial Group module.
    Args:
        k_size: Adaptive selection of kernel size
    """

    def __init__(self, channel, groups=64):
        super(sa_layer, self).__init__()
        self.groups = groups
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.cweight = Parameter(torch.zeros(1, channel // (2 * groups), 1, 1))
        self.cbias = Parameter(torch.ones(1, channel // (2 * groups), 1, 1))
        self.sweight = Parameter(torch.zeros(1, channel // (2 * groups), 1, 1))
        self.sbias = Parameter(torch.ones(1, channel // (2 * groups), 1, 1))

        self.sigmoid = nn.Sigmoid()
        self.gn = nn.GroupNorm(channel // (2 * groups), channel // (2 * groups))

    @staticmethod
    def channel_shuffle(x, groups):
        b, c, h, w = x.shape

        x = x.reshape(b, groups, -1, h, w)
        x = x.permute(0, 2, 1, 3, 4)

        # flatten
        x = x.reshape(b, -1, h, w)

        return x

    def forward(self, x):
        b, c, h, w = x.shape

        x = x.reshape(b * self.groups, -1, h, w)
        x_0, x_1 = x.chunk(2, dim=1)

        # channel attention
        xn = self.avg_pool(x_0)
        xn = self.cweight * xn + self.cbias
        xn = x_0 * self.sigmoid(xn)

        # spatial attention
        xs = self.gn(x_1)
        xs = self.sweight * xs + self.sbias
        xs = x_1 * self.sigmoid(xs)

        # concatenate along channel axis
        out = torch.cat([xn, xs], dim=1)
        out = out.reshape(b, -1, h, w)

        out = self.channel_shuffle(out, 2)
        return out

Results

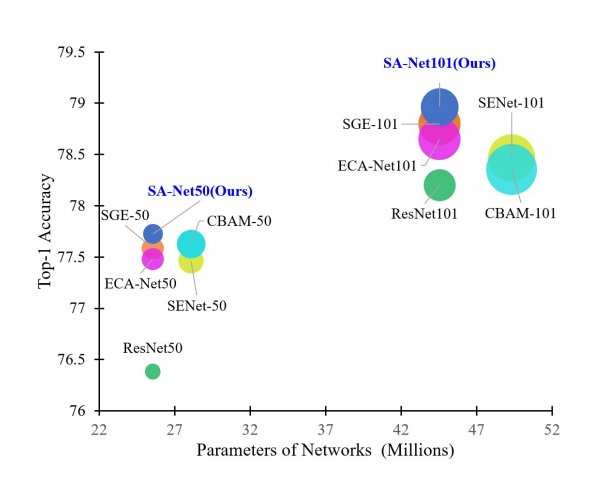
ImageNet-1k classification

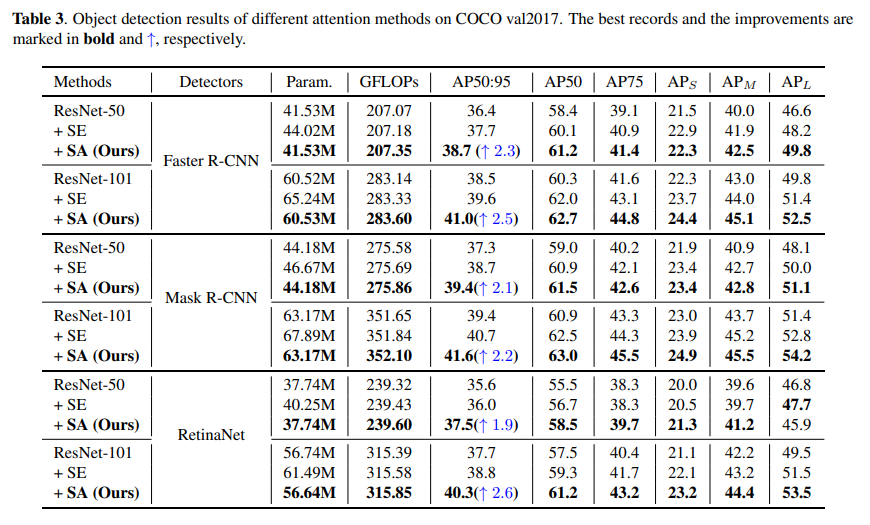
MS-COCO Object Detection

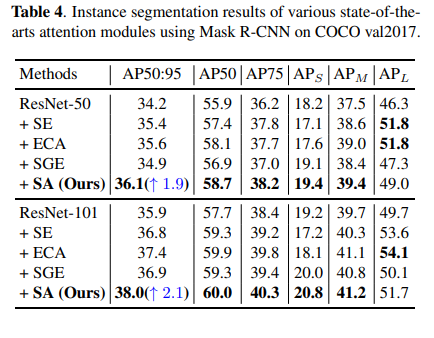
MS-COCO Instance Segmentation

GradCAM visualizations

Conclusion

Shuffle Attention is probably the closest to achieving the right balance between computational overhead and performance boost provided by attention mechanisms. The paper provides solid significant results along with a good background intuition to support the design choices. It would be interesting to see the SA layer being put to the test in more complex and difficult tasks.

References

1. SA-Net: Shuffle Attention for Deep Convolutional Neural Networks
2. SA-Net official GitHub repository