The topic of channel attention mechanisms in computer vision is probably the most widely researched equivalent to Transformers in the domain of natural language processing (NLP). There have been several improvements since the seminal work published in 2018, called Squeeze-and-Excitation Networks, which we covered in this article. Channel Attention methods like Squeeze-and-Excitation have been central to beating benchmarks in leaderboards. For example, the widely popular State of the Art (SOTA) model in ImageNet classification called Efficient Nets lists the Squeeze-and-Excitation module as a crucial component in its architectural design. The value of channel attention mechanisms is not just from the perspective of performance boosts, but also from an interpretability point of view.
Table of Contents
- Why Should You Consider Channel Attention Mechanisms?
- SRM Motivation
- Main Contributions
- Style Recalibration Module (SRM)
a. Style Pooling
b. Style Integration
c. Complexity
d. Comparison with SENets
e. Comparison with ECANets - Code
- Results
- Critical Comments
- Conclusion
- References
Bring this project to life
Why Should You Consider Channel Attention Methods?
Let's make sure we are on the same page in terms of how we evaluate an attention mechanism (in this case, those falling into the category of channel-based attention methods). The term "channel" (referred to as $C$) is defined as the individual feature maps in the (usually) four-dimensional tensor input to, or output of, any intermediate convolution layers in any deep convolutional neural network (CNN). Providing attention to these "channels" essentially means specifying which channel out of the bunch is more or less important, and subsequently assigning it a score or weighing it with a learned attention magnitude. Thus, channel attention methods essentially specify "what to focus on" for the network during the training process. These modules have been evaluated from a perspective of explainability by using GradCAM and GradCAM++, which reveal that networks equipped with channel attention methods have tighter bounds on the label-specific objects in the image.
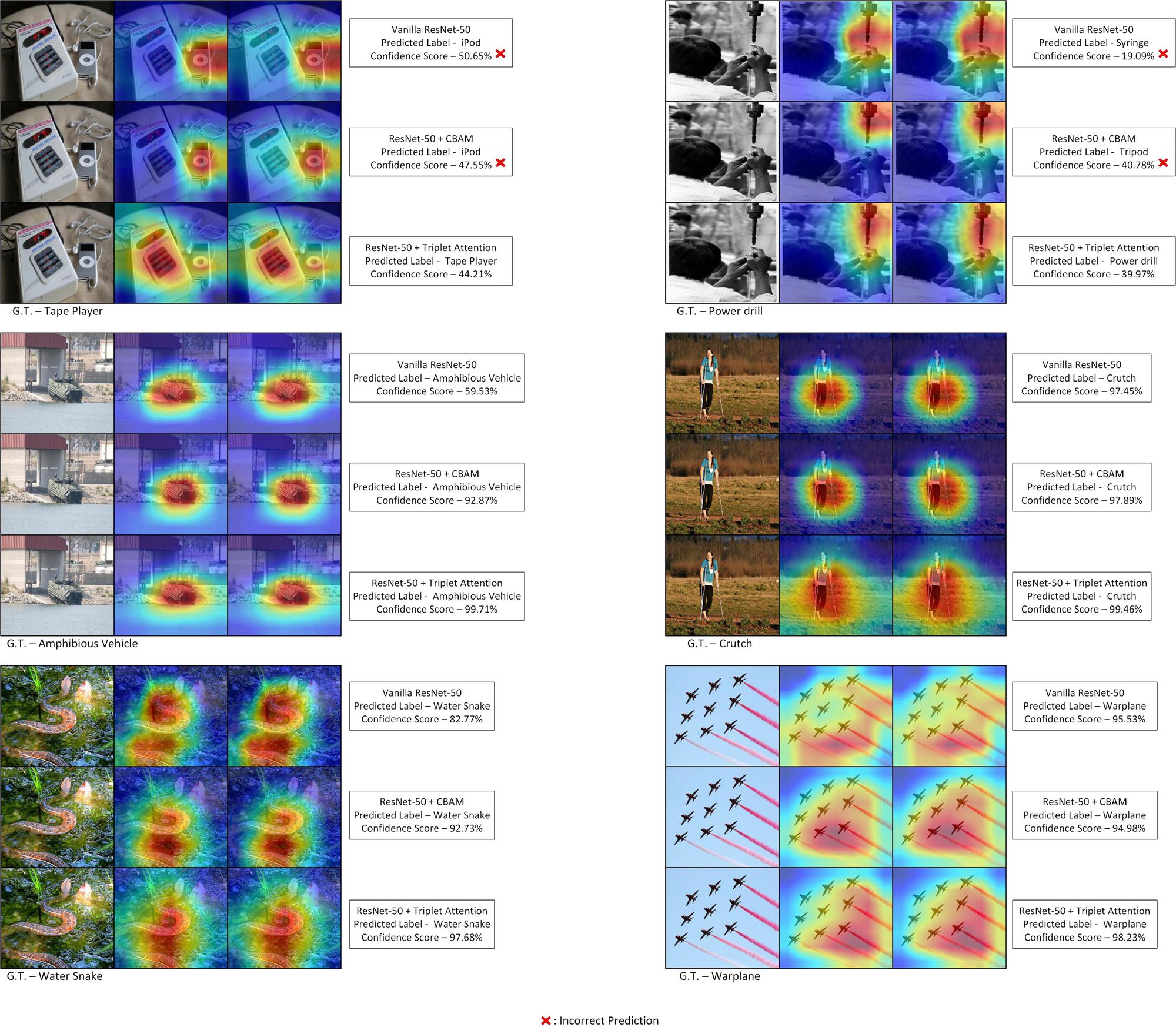
The second reason to consider channel attention methods is that one can use channel attention to do dynamic channel pruning or gating to reduce effective network size or dynamic computation complexity, while maintaining near-constant performance. There have been many approaches in this direction, one of the most recent and prominent being the ICLR 2020 paper by Qualcomm titled Batch-shaping for learning conditional channel gated networks.
One of the main drawbacks in this space is the computational overhead added by these channel attention modules. Although most of these methods are simple plug-and-play modules that can be inserted at any position in a deep CNN, they usually add a significant amount of additional parameters and FLOPs to the model architecture. This also results in increased latency and lower throughput. However, there have been several approaches to reduce overhead costs introduced by these modules which have successfully demonstrated that competitive performances can be achieved with simple low-cost modular channel attention methods.
Given the above information, let's get into the main agenda for this article. We will review yet another channel attention method inspired by the popular Squeeze-and-Excitation Networks (SENets; TPAMI and CVPR 2018), called the Style Recalibration Module (SRM) proposed in the paper by Lee et. al. titled SRM: A Style-based Recalibration Module for Convolutional Neural Networks. Without further ado, we will dive into the motivation of SRM, followed by an analysis of the structural design of the module, and then finally wrap it up by investigating the results along with its PyTorch code.
Abstract
Following the advance of style transfer with Convolutional Neural Networks (CNNs), the role of styles in CNNs has drawn growing attention from a broader perspective. In this paper, we aim to fully leverage the potential of styles to improve the performance of CNNs in general vision tasks. We propose a Style-based Recalibration Module (SRM), a simple yet effective architectural unit, which adaptively recalibrates intermediate feature maps by exploiting their styles. SRM first extracts the style information from each channel of the feature maps by style pooling, then estimates per-channel recalibration weight via channel-independent style integration. By incorporating the relative importance of individual styles into feature maps, SRM effectively enhances the representational ability of a CNN. The proposed module is directly fed into existing CNN architectures with negligible overhead. We conduct comprehensive experiments on general image recognition as well as tasks related to styles, which verify the benefit of SRM over recent approaches such as Squeeze-and-Excitation (SE). To explain the inherent difference between SRM and SE, we provide an in-depth comparison of their representational properties.
Motivation
One of the heavily explored domains in generative modeling is image stylizing. Several influential works have shown the potential of harnessing style context for image-based style transfers. Although these images might look to be more of an aesthetic pleasure, the foundation underneath is crucial in understanding the way convolutional networks work. The underlying potential of style properties in a conv net has also been investigated in discriminative settings. Few works have shown that a conv net constrained to only rely on style information without considering spatial context does quite well on the image classification task.
Style properties serve as one of the two motivating factors for this work, as the authors state:
In this work, we further facilitate the utilization of styles in designing a CNN architecture. Our approach dynamically enriches feature representations by either highlighting or suppressing style regarding its relevance to the task.
In addition to style properties, attention/feature recalibration mechanisms serve as the other piece to the puzzle. In acknowledgment of the shortcomings of previous attention mechanisms like Gather Excite, Squeeze Excite, etc., the paper proposes a novel lightweight efficient channel attention mechanism:
In contrast to the prior efforts, we reformulate channel-wise recalibration in terms of leveraging style information, without the aid of channel relationship nor spatial attention. We present a style pooling approach which is superior to the standard global average or max pooling in our setting, as well as a channel-independent style integration method which is substantially more lightweight than fully connected counterparts yet more effective in various scenarios.
Contributions
The main contributions of this paper are as follows:
We present a style-based feature recalibration module which enhances the representational capability of a CNN by incorporating the styles into the feature maps.
Despite its minimal overhead, the proposed module noticeably improves the performance of a network in general vision tasks as well as style-related tasks.
Through in-depth analysis along with ablation study, we examine the internal behavior and validity of our method.
Style Recalibration Module
In this section we will dissect the exact structural design of the SRM module proposed in the paper and compare it with the traditional Squeeze-and-Excite module.
The Style Recalibration Module (SRM) is made up of two integral components, called Style Pooling and Style Integration. Style Pooling is responsible for generating Style Features $T$ of dimensions $(C \ast d)$ from the input tensor $X$ of dimension $(C \ast H \ast W)$. These Style Features are then passed to the Style Integration phase to generate the Style Weights $G$ of shape $(C \ast 1)$. The Style Weights are then used to recalibrate the channels in the input tensor $X$ by simply element-wise multiplying $X$ with $G$.
In the following sections we will analyze both components of SRM, namely Style Pooling and Style Integration. We will conclude by revisiting Squeeze-and-Excitation Networks and observe the differentiating points between SRM and SE channel attention.
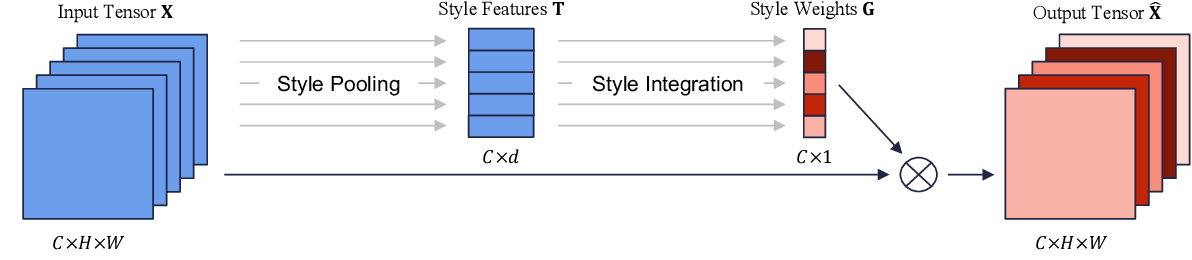
Style Pooling
SRM is made up of two distinct sub-modules responsible for feature decomposition and feature recalibration, respectively. Style Pooling is one of the two components responsible for feature decomposition. In an ideal and optimal setting, it's imperative to process all information available for improved spatial modeling. However, the computational overhead introduced by computing attention maps for every pixel in the tensor is huge. The input tensor is usually a three-dimensional one, $(C \ast H \ast W)$ (excluding batch size). Thus, computing attention maps for every pixel would result in a tensor of size $(C*H*W) \ast H \ast W$, which is a huge number and results in huge memory overhead. This is in fact the foundation of Self Attention, which is considered an integral component of Self Attention Generative Adversarial Networks (SAGAN) and Transformers in the domain of Natural Language Processing (NLP).
Mathematically, Style Pooling takes an input feature map $\textbf{X} \in \mathbb{R}^{N \ast C \ast H \ast W}$ and provides the style pooled features $\textbf{T} \in \mathbb{R}^{N \ast C \ast 2}$ via the following operations:
$\mu_{nc} = \frac{1}{HW}\sum^{H}_{h=1}\sum^{W}_{w=1}{x_{nchw}}$
$\sigma_{nc}= \sqrt{\frac{1}{HW}\sum^{H}_{h=1}\sum^{W}_{w=1}{(x_{nchw} - \mu_{nc})}^{2}}$
$t_{nc}=[\mu_{nc}, \sigma_{nc}]$
The resultant $t_{nc} \in \mathbb{R}^{2}$, denoted as the style vector, serves as the summarization of the style information for each image in batch $n$ and channel $c$. The $\mu_{nc}$ is popularly referred to as Global Average Pooling (GAP) and is also used as the preferred form of compression in other standard attention mechanisms, like Squeeze-and-Excitation (SENets) and Convolutional Block Attention Module (CBAM). The authors do investigate other forms of style pooling, like computing the max pooling which is used along with average pooling in CBAM, in the appendix (this is discussed later in the results section of this article). In the context of style disentanglement, often the correlation between the channels are computed, however, the focus of the authors in this case was to focus on the channel-wise statistics for efficiency and conceptual clarity since computing the channel correlation matrix has a $C \ast C$ computational budget requirement.
Style Integration
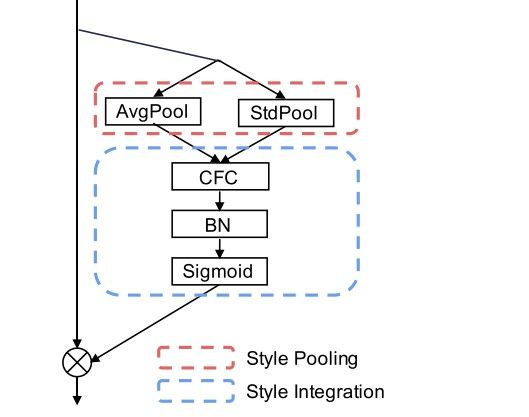
The goal of the style integration module is to model the importance of the styles associated with individual channels to emphasize or suppress them accordingly. Essentially, in a feature map tensor, there is always an unbalanced distribution of the importance of the channels. Some channels might be more influential in contributing to the performance of the model, while others might be simply surplus to the requirements. However, the way vanilla convolutional neural networks are designed, they inherently prioritize each channel equally and give them a channel weight coefficient of one. The Style Integration module essentially tells the network which channels are more important in the complete feature map tensor.
The architectural design of the Style Integration module is showcased in the image above. It is a stack of three blocks:
- Channel-wise fully connected layer (CFC)
- Batch normalization layer (BN)
- Sigmoid activation unit
Mathematically, given the output of the style pooling which is denoted as the style representation $\textbf{T} \in \mathbb{R}^{N \ast C \ast 2}$, the style integration operator encodes channels using learnable parameters $\textbf{W} \in \mathbb{R}^{C \ast 2}$:
$z_{nc}=\textbf{w}_c \cdot \textbf{t}_{nc}$
Where $\textbf{Z} \in \mathbb{R}^{N \ast C}$ denotes the encoded style features. This can be interpreted as a channel-independent fully connected layer with two input nodes and a single output, where the bias term is incorporated into the subsequent BN layer.
Then the output of the CFC is passed to the Batch Normalization layer to improve training. Subsequently, the BN layer's output is passed to a sigmoid activation unit as a gating mechanism, as represented in the following mathematical equations:
$\mu_c^{(z)} = \frac{1}{N}\sum^{N}_{n=1}{z_{nc}}$
$\sigma_c^{(z)} = \sqrt{\frac{1}{N}\sum^{N}{n=1}(z_{nc}-\mu_c^{(z)})^{2}}$
$\tilde{z}_{nc}=\gamma_{c}(\frac{z_{nc}-\mu_c^{(z)}}{\sigma_c^{(z)}})+ \beta_c$
$g_{nc}=\frac{1}{1+e^{-\tilde{z}_{nc}}}$
$\gamma$ and $\beta \in \mathbb{R}^C$ denote the affine transformation parameters, while $\textbf{G} \in \mathbb{R}^{N \ast C}$ represents the learned per-channel style weights.
Note that BN makes use of fixed approximations of mean and variance at inference time, which allows the BN layer to be merged into the preceding CFC layer.
In simpler terms, the Style Integration for each channel in the input feature tensor is a single CFC layer $f_{CFC}: \mathbb{R}^{2} \to \mathbb{R}$ followed by an activation function $f_{ACT} : \mathbb{R} \to [0, 1]$. Finally, the sigmoid activated per-channel style weights are then element-wise multiplied with the individual corresponding channels in the input feature tensor. So the output $\hat{\textbf{X}} \in \mathbb{R}^{N \ast C \ast H \ast W}$ is obtained by:
$\tilde{\textbf{x}}_{nc} = g_{nc} \cdot \textbf{x}_{nc}$
Complexity
One of the objectives of the authors was to design a lightweight and efficient module, both in terms of memory and computational complexity. The two modules which contribute to parametric overhead are the CFC and BN layers. The number of parameters for each term is $\sum{s=1}{S}N_{s} \cdot C_{s} \cdot 2$ and $\sum{s=1}{S}N_{s} \cdot C_{s} \cdot 4$, respectively, where $S$ denotes the number of repeated blocks in the $\textit{s}$-th stage of the architecture, and $C_s$ denotes the dimension of the output channels for the $\textit{s}$-th stage. In total, the number of parameters contributed by SRM is:
$6\sum^{S}_{s=1}N_s \cdot C_s$
If Resnet-50 is considered as a baseline architecture, then adding SRM to every block of the architecture results in an additional 0.02 GFLOPs and 0.06M more parameters. This is significantly cheaper than other standard attention mechanisms like SENets, which adds 2.53M more parameters when used in the same ResNet-50 architecture.
Comparison With Squeeze-and-Excitation Nets (SENets)
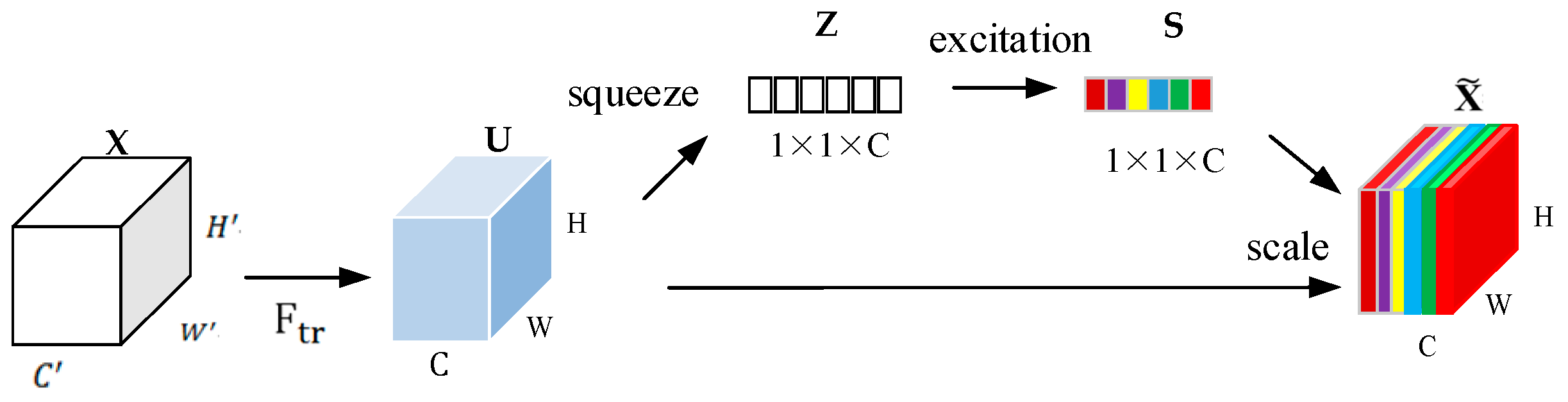
Squeeze-and-Excitation Networks (SENets) serve as one of the most fundamental attention mechanisms in the domain of computer vision. Most modern architectures using attention modules have been inspired by the prominent SENets in one way or another, and SRM is no exception. There are a few key distinctions between the SRM module and the SE module. While both modules have feature compression and feature weighting methods, the exact processes involved are different for SE and SRM. SRM retains the average pooling used in the SE's squeeze module, however, it adds a standard deviation pooling to it for richer feature representation upon compression.
Additionally, another major difference comes in the feature weighting module of SRM. In the case of SE, the feature weighting module (which is called the "excitation" module) uses a multi-layer perceptron bottleneck, which first reduces the dimensionality and then expands it back again. This majorly contributes to the parametric overhead introduced by SE in the backbone architecture being used. However, in the case of SRM, it uses a CFC which is significantly cheaper than the MLP used in SE, and that's the major reason why SRM is so cheap compared to SE. Alas, both SRM and SE use the sigmoid activation unit to scale the learned per-channel weights, and then element-wise multiply these scaled weights to the corresponding channels in the input feature tensor.
To understand the representational differences between SE and SRM, the authors visualized the features learned by both SRM and SE through the images which lead to the highest channel weights. They did this by using an SE and SRM based ResNet-56 trained on the DTD dataset. As shown in the figure below, SE results in highly overlapping images across channels, while SRM demonstrates a higher diversity in top-activated images, which implies that SRM allows a lower correlation between channel weights as compared to SE. The authors further imply that the difference between the representative expressive powers of SE and SRM can be a future area of research. Although the distinction is significant, it didn't necessarily provide complete clarity on the impact of the different modules in SRM compared to that of SE, because of the extreme similarity between the two structures in terms of design.
To quote the authors:
The conspicuous grid pattern in SE’s correlation matrix implies that groups of channels are turned on or off synchronously, whereas SRM tends to encourage decorrelation between channels. Our comparison between SE and SRM suggests that they target quite different perspectives of feature representations to enhance performance, which is worth future investigation.

Comparison With Efficient Channel Attention Nets (SENets)
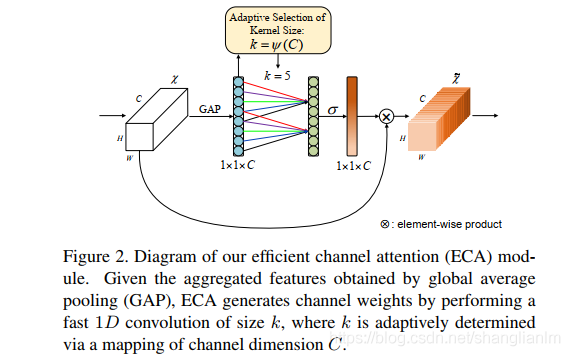
On paper, ECANets seem to be a replica of SRM while only offering minute modifications at best, which haven't been well justified. ECA is incredibly cheap, and cheaper than SRM, because of two primary reasons. In the case of ECA, the feature compression method only involves that of GAP (Global Average Pooling), similar to that of SE, while SRM uses both the GAP and standard deviation pooling. Furthermore, ECA doesn't rely on a batch normalization layer while SRM uses one right after the CFC layer. There is one more caveat to the structure of ECA, as it uses an adaptive kernel size formula for the 1-D conv layer, which is used for feature weighting. This formula contains two hyperparameters $\gamma$ and $b$ which are predefined for the best performance, and are adaptively tuned based on the number of channels $C$ in the input feature map tensor.
Code
Following is the PyTorch code for the SRM module that can be plugged into a standard convolutional backbone architecture:
import torch
from torch import nn
class SRMLayer(nn.Module):
def __init__(self, channel, reduction=None):
# Reduction for compatibility with layer_block interface
super(SRMLayer, self).__init__()
# CFC: channel-wise fully connected layer
self.cfc = nn.Conv1d(channel, channel, kernel_size=2, bias=False,
groups=channel)
self.bn = nn.BatchNorm1d(channel)
def forward(self, x):
b, c, _, _ = x.size()
# Style pooling
mean = x.view(b, c, -1).mean(-1).unsqueeze(-1)
std = x.view(b, c, -1).std(-1).unsqueeze(-1)
u = torch.cat((mean, std), -1) # (b, c, 2)
# Style integration
z = self.cfc(u) # (b, c, 1)
z = self.bn(z)
g = torch.sigmoid(z)
g = g.view(b, c, 1, 1)
return x * g.expand_as(x)As for TensorFlow, SRM can be defined as follows:
import tensorflow as tf
def SRM_block(x, channels, use_bias=False, is_training=True, scope='srm_block'):
with tf.variable_scope(scope) :
bs, h, w, c = x.get_shape().as_list() # c = channels
x = tf.reshape(x, shape=[bs, -1, c]) # [bs, h*w, c]
x_mean, x_var = tf.nn.moments(x, axes=1, keep_dims=True) # [bs, 1, c]
x_std = tf.sqrt(x_var + 1e-5)
t = tf.concat([x_mean, x_std], axis=1) # [bs, 2, c]
z = tf.layers.conv1d(t, channels, kernel_size=2, strides=1, use_bias=use_bias)
z = tf.layers.batch_normalization(z, momentum=0.9, epsilon=1e-05, center=True, scale=True, training=is_training, name=scope)
# z = tf.contrib.layers.batch_norm(z, decay=0.9, epsilon=1e-05, center=True, scale=True, updates_collections=None, is_training=is_training, scope=scope)
g = tf.sigmoid(z)
x = tf.reshape(x * g, shape=[bs, h, w, c])
return xIn both, during initialization of the layer in the architecture, be sure to pass the correct channel number as the parameter to that layer.
Results
In this section, we will take a look at the various results showcased by the authors, ranging from image classification on ImageNet and CIFAR-10/100 to style transfer and texture classification.
ImageNet-1k
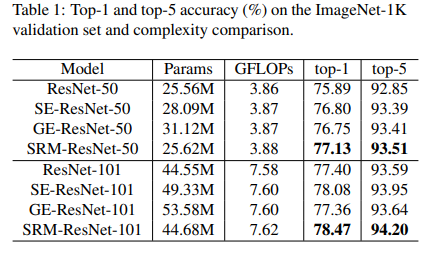
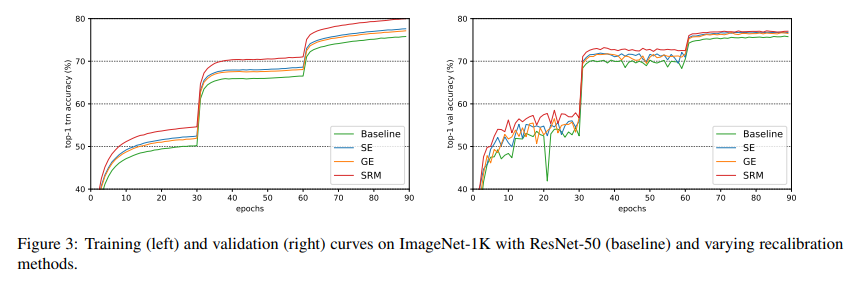
As shown in the above table, SRM substantially outperforms vanilla, GE, and SE-based networks on the ImageNet classification task while being cheap in terms of parametric overhead. The training curves for the ResNet-50 based models are shown in the graph below:
The authors also tested SRM on Stylized ImageNet, a variant of ImageNet created using images stylized by a random painting in the Painter by Numbers dataset. More details about the datasets and the training settings can be found in the paper.
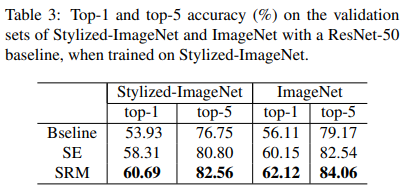
Similar to the previous results on ImageNet, SRM holds a strong place in the case of Stylized ImageNet, as showcased in the above table.
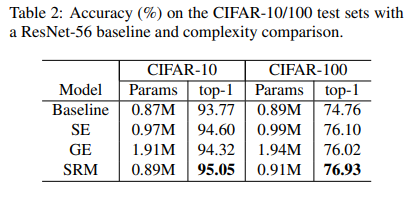
CIFAR 10/100
SRM was also able to maintain a comfortable lead over Vanilla, SE, and GE (Gather Excite) variants on CIFAR-10 and CIFAR-100 image classification benchmarks, as shown in the table below:
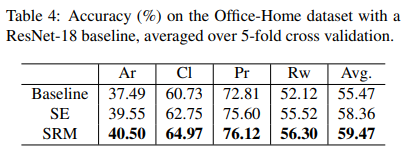
Office Home Dataset
SRM also demonstrated consistently better performance than baseline and SE-based ResNet-18 on multi-domain classification on the Office Home dataset on average over 5-fold cross-validation. Results are shown in the table below:
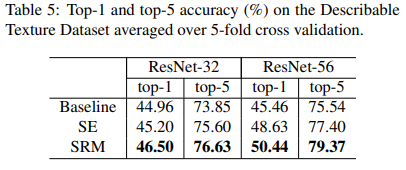
Texture Classification
Continuing with the strong performances demonstrated in the benchmarks discussed above, SRM improved the scores of ResNet-32 and ResNet-56 models over the baseline and SE variants on the texture classification benchmark on the Describable Texture Dataset averaged over 5-fold cross-validation, as shown below:
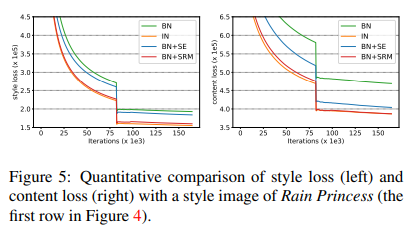
Style Transfer
The authors finally explored the performance of SRM on the task of style transfer using the MS-COCO dataset. The training graph and sample outputs for quantitative analysis are presented below:

And some more examples:

Ablation Study
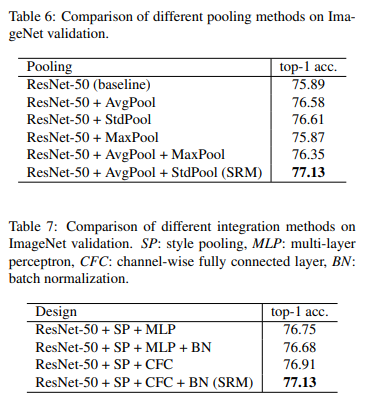
To further understand the importance of the different components used in SRM, the authors conducted an extensive study on the pooling methods and style integration methods used in SRM, which are showcased in the tables below:
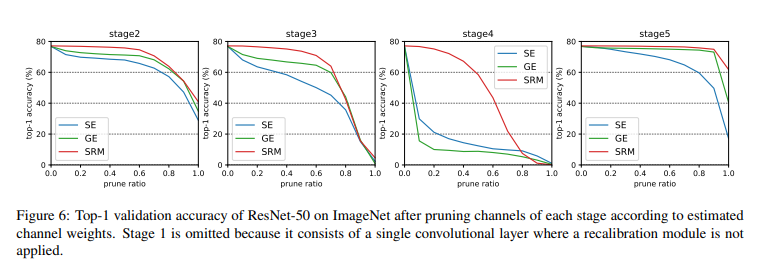
Finally, to validate that SRM yields relevant channel weights, the authors used SRM's channel weights to prune the model and observed the sparse (pruned) model's performance. As shown in the graph below, SRM-based pruned networks demonstrate improved performance compared to baseline:
Critical Comments
Overall, the paper is extremely thoroughly written. Due credits to the authors, they have provided a wide range of experimental results along with extensive ablation studies and comparison with SENets. However, with the fast-flowing field of attention mechanisms in computer vision, most methods get obscured by the new variants coming out each year. Although the paper doesn't necessarily showcase any drawbacks or shortcomings, as with every attention method, it involves an increase in computational cost. Alas, it remains to the judgement of the user to give it a try on their own task/dataset.
Conclusion
The Style Recalibration Module (SRM) is an efficient and lightweight channel attention module that provides significantly improved and competitive performance across a wide range of tasks using deep convolutional neural networks. SRM can be considered a strong substitute to the evergreen Squeeze-and-Excitation modules currently employed in different State of the Art (SOTA) networks, like Efficient Nets.











