As defined by several authors (Wason and Johnson-Laird, 1972; Wason, 1968; Galotti, 1989; Fagin et al., 2004; McHugh and Way, 2018), reasoning is the act of thinking about something logically and systematically in order to draw a conclusion or make a decision. Inference, evaluation of arguments, and logical conclusion-drawing are all components of reasoning.
"Reasoning" is a term that appears often in literature and everyday conversation, but it is also a vague idea that can mean several things depending on the context. We provide a brief summary of various widely accepted types of reasoning to assist the reader grasp this notion.
Different types of reasoning
Deductive reasoning: In deductive reasoning, one draws a conclusion by assuming the validity of the premises. Since the conclusion in deductive reasoning must always flow logically from the premises, if the premises are true, then the conclusion must also be true.
Inductive reasoning: A conclusion is reached by inductive reasoning when supporting evidence is considered and accepted.Based on the facts provided, it is probable that the conclusion is correct, but this is by no means a guarantee.
Example:
Observation: Every time we see a creature with wings, it is a bird.
Observation: We see a creature with wings.
Conclusion: The creature is likely to be a bird.
Abductive reasoning: In abductive reasoning, one seeks the most plausible explanation for a collection of observation in order to arrive at a conclusion. This conclusion is based on the best available information and represents the most plausible explanation; nonetheless, it should not be taken as absolute fact.
For example:
• Observation: The car cannot start and there is
a puddle of liquid under the engine.
• Conclusion: The most likely explanation is that the car has a leak in the radiator
Other types of reasoning include analogical reasoning, which involves making comparisons between two or more things in order to make inferences or arrive at conclusions; causal reasoning, which involves identifying and understanding the causes and effects of events or phenomena; and probabilistic reasoning, which involves making decisions or arriving at conclusions based on the likelihood or probability of certain outcomes.
Formal Reasoning vs Informal Reasoning: In mathematics and logic, the term "formal reasoning" refers to a certain type of reasoning that is both methodical and logical. In daily life, we often utilize a style of reasoning known as "informal reasoning," which is a less formal method that relies on intuition, experience, and common sense to make conclusions and solve issues. While informal reasoning is more flexible and open-ended, it may be less reliable than formal reasoning due to its lack of structure.
Reasoning in Language Models: While the concept of reasoning in language models is not new, there is not a clear definition of what it entails. Although it is not always made clear that the reasoning in question is informal (Cobbe et al., 2021; Wei et al., 2022b, among others), the word "reasoning" is often used to refer to such reasoning in the literature.
Towards Reasoning in Large Language Models
It is well acknowledged that language models and other NLP models struggle with reasoning, especially multi-step reasoning (Bommasani et al., 2021; Rae et al., 2021; Valmeekam et al., 2022). At a certain size, such as models with over 100 billion parameters, recent research has revealed that reasoning capacity may arise in language models (Wei et al., 2022a,b; Cobbe et al., 2021). In this paper the authors follow Wei et al. (2022a) in considering reasoning as an ability that is rarely present in small- scale models like GPT-2 (Radford et al., 2019) and BERT (Devlin et al., 2019), and therefore focus on techniques applicable to improving or eliciting "reasoning" in LLMs such as GPT-3 (Brown et al., 2020) and PaLM (Chowdhery et al., 2022).
Fully Supervised Finetuning
It is important to note that, there is an ongoing research of improving reasoning in small language models by means of fully supervised finetuning on targeted datasets. Models trained with explanations perform better on commonsense question answering tasks (Talmor et al., 2019), as shown by the work of Rajani et al. (2019), who fine tuned a pretrained GPT model (Radford et al., 2018) to provide rationales that explain model predictions using the constructed CoS-E dataset.
Fully supervised fine-tuning suffers from two serious flaws. It first requires a dataset with explicit reasoning, which can be challenging and time-consuming to generate. Furthermore, the model is restricted to a single dataset for training, limiting its use to a single domain and increasing the likelihood that it would depend on artifacts in the training data rather than true reasoning to generate predictions.
Prompting & In-Context Learning
Through in-context learning, large language models like GPT-3 (Brown et al., 2020) have shown amazing few-shot performance on a wide range of tasks. A query and some "input, output" examples are all that's needed to get these models "reasoning" about how to approach an issue and find a solution, either implicitly or explicitly. While these models have improved, they still struggle with problems that call for multiple steps of reasoning to resolve (Bommasani et al., 2021; Rae et al., 2021; Valmeekam et al., 2022). Recent research has revealed that this might be because the full potential of these models has not been explored.
Chain of Thought and Its Variants
By instructing LLMs to engage in "reasoning" explicitly, we can increase the likelihood that they will reason rather than merely provide answers.
Wei et al. (2022b) suggest using chain-of-thought prompting as a means to this end. The "chain of thought" (CoT) examples provided in this method represent intermediary steps in the process of thinking using natural language.
Specifically, in CoT prompting, ⟨input, output⟩ demonstrations are replaced with
⟨input, chain of thought, output⟩ triples
Examples
[input] Roger has 5 tennis balls. He buys 2 more cans
of tennis balls. Each can has 3 tennis balls. How
many tennis balls does he have now?
[chain of thought] Roger started with 5 balls. 2 cans of 3
tennis balls each is 6 tennis balls. 5 + 6 = 11.
[output] The answer is 11.”
As a result, when presented with a target question, the model learns to produce clear rationales before generating the final response. In the literature, various types of chain-of-thought prompting have been developed, each in a distinct form or to tackle a particular issue.
Different Form: In order to elicit reasoning without the necessity for few-shot demonstrations, Kojima et al. (2022) propose Zero-shot-CoT, in which LLMs are merely prompted with the statement "Let's think step by step" following the input. Madaan et al. (2022); Gao et al. (2022); and Chen et al. (2022) discover that LLMs trained with code, such as Codex (Chen et al., 2021), perform better on reasoning tasks when reasoning is framed as code generation.
Specific Problem/Setting: Prior to chain of thought, Nye et al. (2022) attempt to use intermediate computations dubbed "scratchpads" to enhance language models' reasoning performance in both finetuning and few-shot regimes, with a particular emphasis on programs. Shi et al. (2022) try to solve multilingual reasoning problems using CoT in the original language, CoT in English (independent of the problem language), and CoT in English (with the problem translated to English).
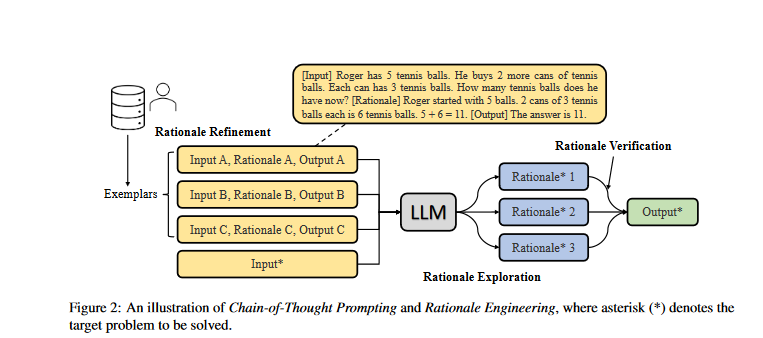
Rationale Engineering
Rationale engineering attempts to improve the elicitation or use of reasoning in LLMs. This can be achived by rationale refining (creating more effective examples of reasoning processes) or rationale exploration and rationale verification (exploring and evaluating the rationales given by LLMs). Figure 2 depicts an overview of raltionale engineering.
Rationale refinement: The goal of rationale refinement is to generate and enhance rationale examples that are more capable of eliciting reasoning in LLMs. Fu et al. (2022b) suggest using complexity-based prompting to generate rationales with more reasoning processes. Their findings suggest that, when rationale complexity increases, LLM performance improves. Similarly, Zhou et al.(2022c) propose algorithmic prompting, which implies that, presenting more detailed examples of solutions can aid in improving reasoning ability on certain easy arithmetic computations.
Rationale exploration: In addition to offering better exemplars, we can enable LLMs to completely explore multiple modes of reasoning in order to enhance their performance on reasoning tasks: This process is known as rationale exploration. Wang et al. (2022c) introduce a decoding technique termed self-consistency to improve on the classic greedy decoding utilized in chain-of-thought prompting. This technique includes sampling a varied range of rationales rather than simply the greedy one and finding the most consistent response by marginalizing out the sampled rationales.
Rationale verification: The accuracy of LLM predictions relies on the accuracy of the rationales used to arrive at such predictions, hence checking their validity is essential (Ye and Durrett, 2022). To solve this problem, a process called rationale verification has been developed to check whether LLMs' explanations of their reasoning really result in accurate answers. To improve LLMs' performance in answering mathematical word problems, Cobbe et al. (2021) propose adding a trained verifier that ranks each LLM's reasoning and solution and chooses the solution with the highest score.
Problem Decomposition
Despite its success in eliciting reasoning in LLMs, chain-of-thought prompting might struggle with complex problems, such as those that need compositional generalization (Lake and Baroni, 2018; Keysers et al., 2020). To handle a complex problem, it is sometimes advantageous to partition it into simpler parts. Each of these subproblems must be resolved before the larger problem can be resolved successfully. Decomposition, sometimes known as "divide and conquer," describes this method.
least-to-most prompting: Zhou et al. (2022a) propose least-to-most prompting, which entails two steps: first, breaking down the complex problem into manageable subproblems; second, solving these subproblems in a specific order, with the answers to each subproblem facilitating the solution to the next subproblem in the sequence. The dynamic least-to-most prompting introduced by Droz- dov et al. (2022) is a follow-up piece of work that aims to address more realistic semantic parsing issues by dissecting them using prompting-based syntactic parsing and then dynamically choosing exemplars depending on the decomposition.
Decomposed prompting: Khot et al. (2022) propose decomposed prompting, which divides a complex problem into subproblems that can be addressed by a common library of prompting-based LLMs, each specialized in a specific subproblem.
successive prompting: Successive prompting, developed by Dua et al. (2022), is an iterative method of decomposing a complex problem into a series of simpler problems, with each subsequent subproblem prediction having access to the solutions from the prior one.
Others Techniques
- Other techniques have been created to aid reasoning in LLMs for certain tasks or contexts. For example, Creswell et al. (2022); Creswell and Shanahan (2022) provide a selection-inference architecture that use LLMs as modules to choose and infer reasoning steps from a collection of facts, culminating in the final response.
- Instead of forward chaining as Creswell et al. (2022), Kazemi et al. (2022) propose utilizing backward chaining, i.e., from objective to the collection of facts that support it;
- The method developed by Zhou et al. (2022b) for performing numerical reasoning on complex numbers involves substituting complex values with simpler numbers to generate simpler expressions, which are then used to perform computations on the complex numbers.
Li et al. (2022a), Shridhar et al. (2022), and Magister et al. (2022) are only a few examples of researchers that have attempted to condense the logic behind LLMs into more manageable models. In conclusion, we recommend reading the position paper on language model cascade written by Dohan et al. (2022), which provides a unified framework for understanding chain-of-thought prompting and related research.
Hybrids Methods
While "prompting" techniques might assist elicit or better use reasoning in large language models to solve reasoning problems, they do not truly demonstrate the reasoning skills of the LLMs themselves since the model parameters remain unchanged. In contrast, the "hybrid approach" tries to increase the reasoning powers of LLMs while also making greater use of these models to tackle complex issues. This strategy entails both improving the LLMs' reasoning ability and using techniques like prompting to make the most of these abilities.
Reasoning-Enhanced Training and prompting
- Pretraining or fine-tuning the models using datasets that feature "reasoning" is a method that can be used to enhance LLMs' reasoning capabilities. CoT prompting improves the performance of LLMs trained on scientific and mathematical data on reasoning tasks, including quantitative reasoning problems, as shown by Lewkowycz et al. (2022) and Taylor et al. (2022).
- For example, T5 (Raffel et al., 2020) shows improved performance on natural language reasoning tasks including numerical reasoning and logical rea-soning when continuously pretrained using SQL data (Pi et al., 2022).
- Chung et al. (2022) finetune PaLM (Chowdhery et al., 2022) and T5 (Raffel et al., 2020) using 1.8k fine-tuning tasks, including CoT data, and discover that CoT data are essential to maintaining reasoning skills.
Bootstrapping & Self-Improving
Some research has looked at the possibility of letting LLMs develop their own reasoning skills through a process called bootstrapping, as opposed to fine-tuning them on pre-built datasets that already include reasoning.
One example of this is the Self-Taught Reasoner (STaR) introduced by Zelikman et al. (2022), in which a LLM is trained and refined on its own output iteratively. Specifically, with CoT prompting, the model first generates initial rationales. And then, the model is finetuned on rationales that lead to correct answers. This process can be repeated, with each iteration resulting in an improved model that can generate better training data, which in turn leads to further improvements.
Following up on this work, Huang et al. (2022a) demonstrate that LLMs can self-improve their reasoning abilities through the use of self-consistency of reasoning (Wang et al., 2022c), which eliminates the necessity for supervised data.
Measuring Reasoning in Large Language Models
Reporting LLMs' performance (e.g., accuracy) on end tasks that include reasoning is one technique to evaluate their reasoning ability. Here are some industry standards:
Arithmetic Reasoning
Arithmetic reasoning is the capacity to understand and use mathematical concepts and principles in order to solve issues requiring arithmetic operations. When addressing mathematical issues, this entails applying logical reasoning and mathematical concepts to decide the best path of action.
Math (Hendrycks et al., 2021), MathQA (Amini et al., 2019), SVAMP (Patel et al., 2021), AS- Div (Miao et al., 2020), AQuA (Ling et al., 2017), and MAWPS (Roy and Roth, 2015) are all examples of benchmarks for mathematical reasoning.
Commonsense Reasoning
Commonsense Reasoning is the use of everyday knowledge and understanding to make judgments and predictions about new situations. It is a fundamental aspect of human intelligence that enables us to navigate our environment, understand others, and make decisions with incomplete information.
The CSQA (Talmor et al., 2019), StrategyQA (Geva et al., 2021), and ARC (Clark et al., 2018) are all benchmarks that may be used to evaluate an LLM's commonsense reasoning capabilities. For a more comprehensive overview of this field, we suggest reading Bhargava and Ng's paper (2022).
Symbolic Reasoning
Symbolic reasoning is a kind of reasoning in which symbols are manipulated in accordance with formal rules. Symbolic reasoning entails deducing or fixing a problem by manipulating abstract symbols representing ideas and connections in accordance with strict rules. Two benchmarks of symbolic reasoning are presented in Wei et al. (2022b), including Last Letter Concatenation
and Coin Flip.
Others benchmarks
In reality, as long as the downstream tasks includes reasoning, there are several benchmarks that can be used to assess the reasoning ability of LLMs (indirectly). The BIG-bench (Srivastava et al., 2022) comprises over 200 tasks that assess a variety of reasoning abilities, such as Date Understanding, Word Sorting, and Causal Judgement. Other benchmarks, such as SCAN (Lake and Baroni, 2018) and Anil et al. (2022), are concerned with assessing generalization ability.
Benchmarks such as WikiTableQA (Pasupat and Liang, 2015) and FetaQA (Nan et al., 2022) may also be used to assess LMs' table reasoning skills, as recommended by Chen (2022). There are other benchmarks for evaluating the generative relational reasoning abilities of LLMs, such as CommonGen (Lin et al., 2020; Liu et al., 2022a) and Open Relation Modeling (Huang et al., 2022b,d).
Findings and Implications
Here, we provide a concise overview of the key findings and implications of research on reasoning in large language models.Here, we provide a concise overview of the key findings and implications of research on reasoning in large language models:
Reasoning seems an emergent ability of LLMs: Significant increases in performance on reasoning tasks at a particular size (e.g., 100 billion parameters) suggest that reasoning ability seems to arise mainly in large language models like GPT-3 175B (Wei et al., 2022a,b; Suzgun et al., 2022). It's possible that training tiny models for specialized tasks is less efficient than using a large model for general reasoning problems. The underlying cause of this emerging skill, however, remains a mystery. For several possible reasons, we can see Wei et al. (2022a) and Fu et al. (2022a).
Chain of thought elicits “reasoning” of LLMs: In experiments conducted by Wei et al. (2022a,b) and Suzgun et al. (2022), it was found that LLMs performed better when given chain-of-thought (CoT) prompts to help them reason through a problem. Saparov and He (2022) (4.2) show that LLMs can generate correct individual proof steps when presented with CoT prompts, even when the synthetic ontology is fictitious or counterfactual.
When faced with a choice between many options, they can choose the wrong one, which might result in a flawed or incomplete proof. Chain-of-thought prompting can lead to significant performance improvements for many reasoning tasks, including those where the performance of standard prompting rises smoothly with model size. Furthermore, it has been shown that compared to standard prompting or fully supervised finetuning paradigms, using CoT prompts improves the out-of- distribution robustness of LLMs (Wei et al., 2022b; Zhou et al., 2022a; Anil et al., 2022).
LLMs show human-like content effects on reasoning: The reasoning tendencies of LLMs are comparable to those of humans, as described in the cognitive literature, as stated by Dasgupta et al. (2022).
For instance, the models' predictions are affected by factors like familiarity and abstract thinking, while the credibility of the results affects how seriously they are taken as true.
Despite the fact that language models may not always perform well on reasoning tasks, these results imply that their failures typically occur in settings that are tough for humans as well. This suggests that language models may "reason" in a way analogous to human reasoning.
LLMs are still unskilled at complex reasoning: According to research by authors like Valmeekam et al. (2022), Han et al. (2022a), and Ruis et al. (2022), while LLMs seem to have outstanding reasoning ability, they nevertheless struggle with more complex reasoning problems or those requiring implicature.
Right task/application: More realistic and relevant applications, such as decision making (Edwards, 1954), legal reasoning (Levi, 2013), and scientific reasoning (Zimmerman, 2000), are necessary to fully grasp the reasoning capabilities of LLMs. Having LLMs perform operations that are easily accomplished by other programs is not where we want to end up. Research that is significant must always consider the task at hand and whether or not the suggested approach can be applied to other, more realistic problems and applications.
Improving reasoning capabilities of LLMs: Large language models can benefit from techniques such as chain-of-thought prompting (Wei et al., 2022b) to elicit their reasoning skills, but these methods will not allow the models to solve challenges beyond their existing capabilities. Training data, model architecture, and optimization objectives that are geared toward encouraging reasoning are all required to significantly improve reasoning in LLMs. Examples include fine-tuning a model using a dataset that contains CoT data to enhance its reasoning (Chung et al., 2022), and bootstrapping a model's reasoning to enhance its own performance (Zelikman et al., 2022; Huang et al., 2022a). There is still a lot of room for improvement in reasoning in large language models, thus we welcome any and all future research in this field.
Conclusion
Although LLMs have made great strides in natural language processing and related domains, it is still unclear whether or not they are really capable of genuine reasoning or if they are merely use learned patterns and heuristics to solve issues. More study is required to understand LLMs' reasoning skills, enhance LLMs' reasoning powers, and evaluate their prospective uses.
Reference













