Over the past few years, DNNs (Deep Neural Networks) have achieved state-of-the-art performance on several challenging tasks in the domains of computer vision and natural language processing. Driven by increasing amounts of data and computational power, deep learning models have become both wider and deeper to better learn from large amounts of data. But deploying large, accurate deep learning models to resource-constrained or cost-limited computing environments always poses several key challenges.
In this series, you will learn about the need for memory and processing optimizations for Deep CNN (Convolutional Neural Network) models. Then we'll walk through various techniques to run accelerated and memory optimal deep learning model inference, in detail. We'll also discuss various deep learning inference frameworks/libraries needed to reduce the inference cost of deep learning models. We will cover the role of C++ inference accelerator frameworks and libraries, and their Python APIs.
As a prerequisite, this series expects that you have a basic knowledge of Python and CNNs.
Specifically, we'll cover the following topics:
- The need for inference optimization
- Inference optimization techniques: pruning
- Pruning methods and their differences
- Pruning a trained neural network
Bring this project to life
The Need for Inference Optimization
Deep Learning model inference is as important as model training, and is ultimately what controls the performance metrics of the implemented solution. For a given application, once the deep learning model is well-trained, the next step would be to ensure it is deployment/production-ready, which requires both the application and model to be efficient and reliable.
An efficient model is a model that's optimized in terms of both memory utilization and processing speed.
It's essential to maintain a healthy balance between model performance/accuracy and inference time/processing speed. Inference time determines the running cost of the implemented solution. Sometimes the environment/infrastructure/system where your solution will be deployed can also have memory constraints, so it's important to have memory-optimized and real-time (or lower processing time) models.
With the rising use of Augmented Reality, Facial Recognition, Facial Authentication, and Voice Assistants that require real-time processing, developers are looking for newer and more effective ways of reducing the computational costs of neural networks. One of the most popular methods is called pruning.
Pruning Explained
While modern deep CNNs are composed of a variety of layer types, runtime during prediction is dominated by the evaluation of the convolutional layers. To speed up inference, we can "prune" feature maps so that the resulting networks run more efficiently.
Pruning is a popular approach used to reduce heavy networks to lightweight ones by removing redundancies. Simply put, pruning is a way to reduce the size of neural networks.
Biological Inspiration for Pruning
Pruning in neural networks has been taken as an idea from synaptic pruning in the human brain, where axons and dendrites decay and die off between early childhood and the onset of puberty in many mammals, resulting in synapse elimination. Pruning starts near the time of birth and continues into the mid-20s.
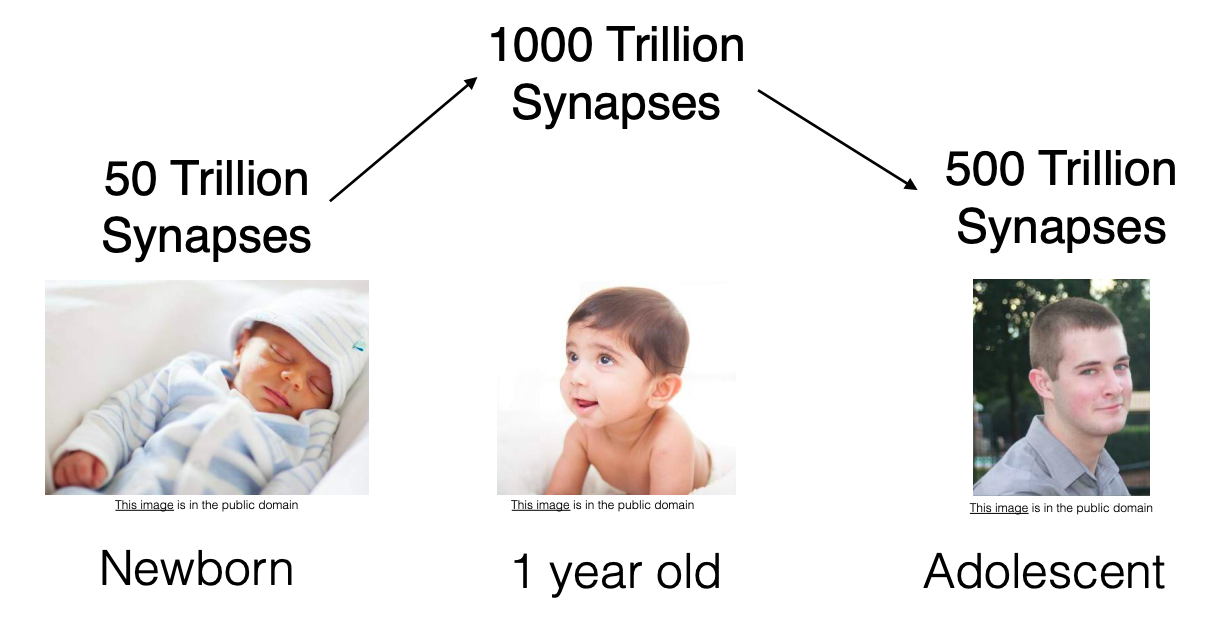
Pruning in Neural Networks
Pruning neural networks is an old idea dating back to 1990, with Yann LeCun's "optimal brain damage" paper. The idea is that among the many parameters in the network, some are redundant and don’t contribute significantly to the output.
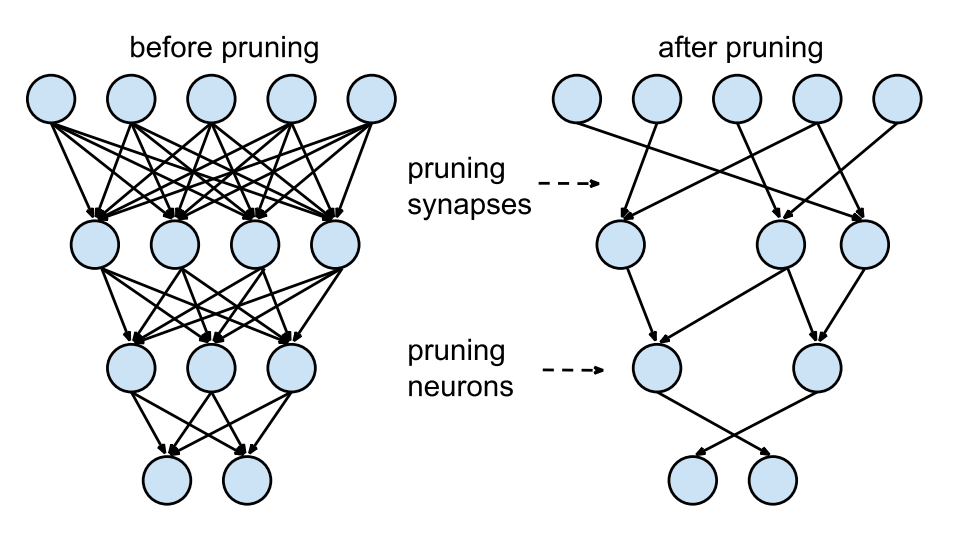
Neural networks generally look like the one on the left: every neuron in the layer below has a connection to the layer above, but this means that we have to multiply a lot of floats together. Ideally, we’d only connect each neuron to a few others and save on doing some of the multiplications; this is called a sparse network.
If you could rank the neurons in the network according to how much they contribute to the output, you could then remove the low-ranking neurons from the network, resulting in a smaller and faster network.
The ranking, for example, can be done according to the L1/L2 norm of neuron weights. After the pruning, the accuracy will drop (hopefully not too much if the ranking is clever), so the network is usually trained again to recover some accuracy. If we prune too much at once, the network might be damaged too much and it won’t be able to recover. So, in practice, this is an iterative process — often called ‘Iterative Pruning’: Prune / Train / Repeat.
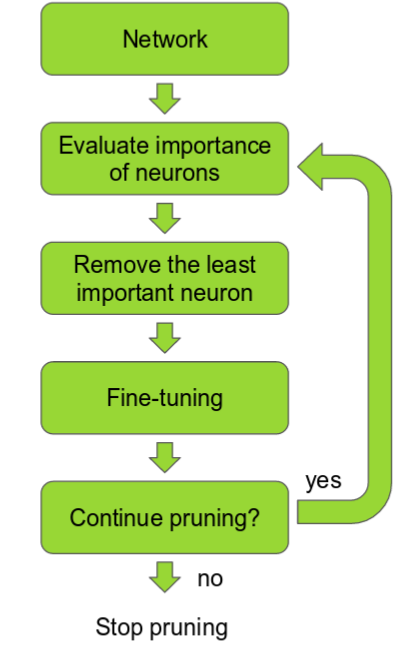
The first step is to determine which neurons are important and which (relatively) are not. After this, the least important neurons will be removed, followed by a fine-tuning of the algorithm. At this point, a decision can be made regarding whether to continue the pruning process or to stop.
It's better to start with a larger network and prune it after training, rather than training a smaller network from the get-go.
Different Pruning Methods
Pruning can come in various forms, with the choice of method depending on the kind of output that is expected from the developer. In some cases speed is prioritized; in others, storage/memory must be reduced. Pruning methods vary primarily in how they handle sparsity structure, scoring, scheduling, and fine-tuning.
In VGG16, for instance, 90% of the weights are in the fully-connected layers, but those account for only 1% of the total floating point operations. Up until recently, most work focused on pruning targeted the fully connected layers. By pruning these layers the model size can be dramatically reduced, but not the processing speed.
Unstructured Pruning methods prune individual parameters. Doing so produces a sparse neural network which, although smaller in terms of parameter count, may not be arranged in a fashion conducive to speed enhancements using modern libraries and hardware. This is also called Weight Pruning as we set individual weights in the weight matrix to zero. This corresponds to deleting connections, as in the figure above (Lecun et al. NIPS’89, Han et al. NIPS’15).
Here, to achieve sparsity of $k%$, we rank the individual weights in a weight matrix $W$ according to their magnitude, and then set the smallest $k%$ to $0$.
Structured Pruning methods consider parameters in groups, removing entire neurons, filters, or channels to exploit hardware and software optimized for dense computation. This is also called Unit/Neuron Pruning, as we set entire columns in the weight matrix to zero, in effect deleting the corresponding output neuron.
In the Pruning Filters for Efficient ConvNets method, they advocate pruning entire convolutional filters. Pruning a filter with index $k$ affects the layer it resides in and the following layer (by removing its input).
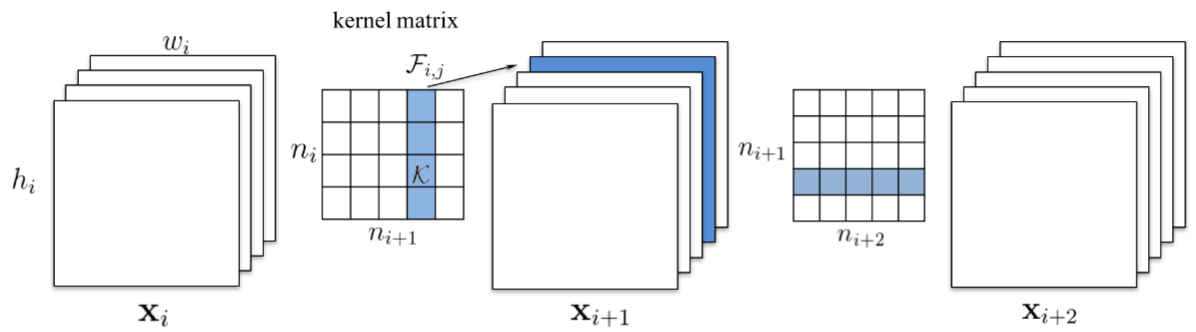
In case the following layer is fully-connected and the size of the feature map of that channel would be $M \times N$, then $M \times N$ neurons are removed from the fully-connected layer. The neuron ranking in this work is fairly simple. It’s the $L1$ norm of the weights of each filter. At each pruning iteration, they rank all the filters, prune the $n$ lowest-ranking filters globally among all the layers, retrain, and repeat.
Pruning entire filters in convolutional layers has the positive side effect of also reducing memory. As observed in the Pruning Convolutional Neural Networks for Resource Efficient Inference paper, the deeper the layer, the more it will get pruned. This means the last convolutional layer will get pruned a lot, and a lot of neurons from the fully-connected layer following it will also be discarded.
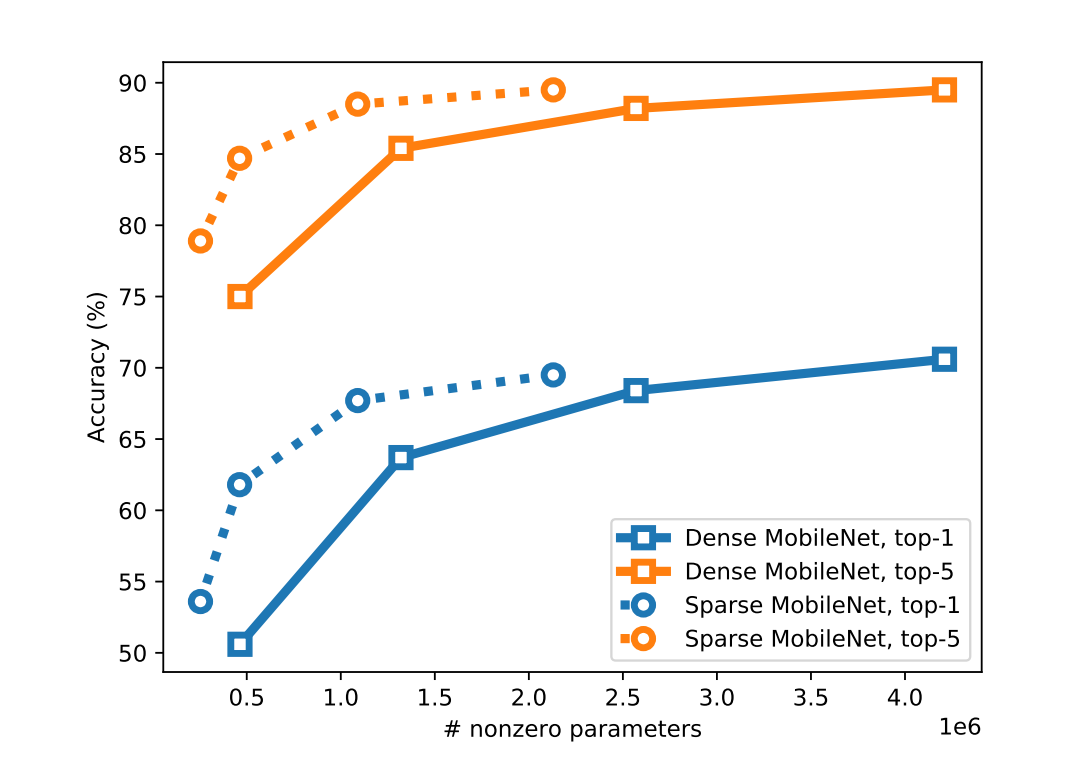
Upon comparing the accuracy of large but pruned models (large-sparse) and their smaller but dense (small-dense) counterparts, with identical memory footprint, across a broad range of neural network architectures (deep CNNs, stacked LSTM, and seq2seq LSTM models), we find large-sparse models to consistently outperform small-dense models and achieve up to a $10 \times$ reduction in the number of non-zero parameters, with minimal loss in accuracy.
Scoring
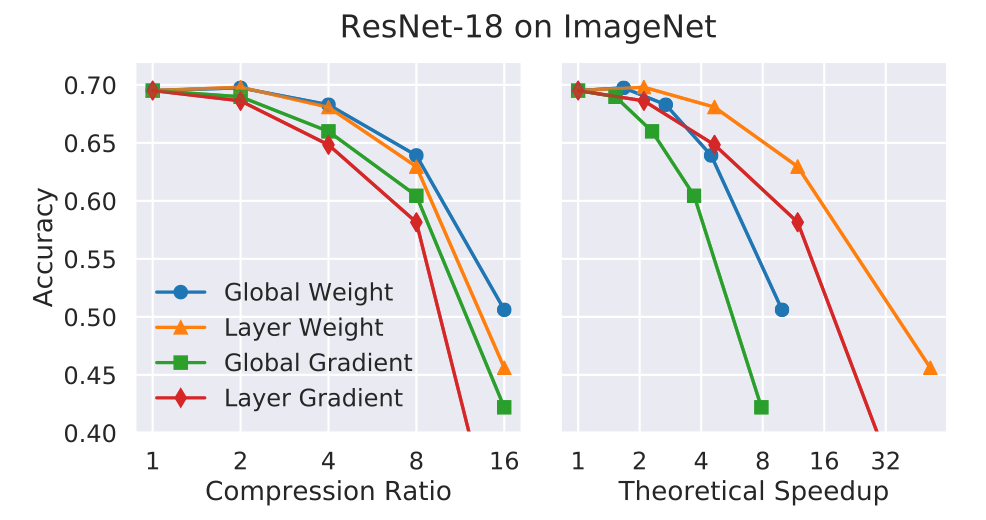
It is common practice to score parameters based on their absolute values, trained importance coefficients, or contributions to network activations or gradients. Some pruning methods compare scores locally, pruning a fraction of the parameters with the lowest scores within each structural subcomponent of the network (e.g. layers). Others consider scores globally, comparing scores to one another irrespective of the part of the network in which the parameter resides.
Ranking is much more complex in the work Structured Pruning of Deep Convolutional Neural Networks. They keep a set of $N$ particle filters, which represent $N$ convolutional filters to be pruned. Each particle is assigned a score based on the network accuracy on a validation set when the filter represented by the particle is not masked out. Then, based on the new score, new pruning masks are sampled. Since running this process is computationally heavy, they used a small validation set for measuring the particle scores.
The method described in Pruning Convolutional Neural Networks for Resource Efficient Inference involves pruning each filter and observing how the cost function changes when the layers are changed. This is a brute force method, and is not very effective without a large amount of compute. However, the ranking method is highly effective and intuitive. It utilizes both the activation and gradient variables as ranking methods, providing a clearer view of the model.
Scheduling
Pruning methods differ in the amount of the network to prune at each step. Some methods prune all desired weights at once in a single step. Others prune a fixed fraction of the network iteratively over several steps, or vary the rate of pruning according to a more complex function.
Fine-tuning
For methods that involve fine-tuning, it is most common to continue to train the network using the trained weights from before pruning. Alternative proposals include rewinding the network to an earlier state and reinitializing the network entirely.
At the time of writing this article, one of the most recent approaches to pruning is SynFlow (Pruning neural networks without any data by iteratively conserving synaptic flow). SynFlow does not require any data for pruning a network, and it uses Synaptic Saliency Scores to determine the significance of parameters.
Evaluating Pruning
Pruning can accomplish many different goals, including reducing the storage footprint of the neural network and the computational cost of inference. Each of these goals favors different design choices and requires different evaluation metrics.
For example, when reducing the storage footprint of the network, all parameters can be treated equally, meaning that one should evaluate the overall compression ratio achieved by pruning. However, when reducing the computational cost of inference, different parameters may have different impacts. For instance, in convolutional layers, filters applied to spatially larger inputs are associated with more computation than those applied to smaller inputs.
Regardless of the goal, pruning imposes a tradeoff between model efficiency and quality, with pruning increasing the former while (typically) decreasing the latter. This means that a pruning method is best characterized not by a single model it has pruned, but by a family of models corresponding to different points on the efficiency-quality curve.
Conclusion
As more and more applications make use of neural networks, lightweight algorithms are the need of the hour. Pruning is one essential method that those working in DL should be aware of and have in their toolkit. In this article we covered what pruning is, how it works, different pruning methods, and how to evaluate them.
Stay tuned for future articles covering how to optimize neural network performance!











